
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метрические соотношения в треугольнике.
Теорема синусов. 1). Стороны треугольника пропорциональны синусам противолежащих углов
2). Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной около треугольника окружности.

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус их удвоенное произведение на косинус угла между ними. 
Формулы площадей фигур и длины окружности.
| треугольник | параллелограмм | прямоугольник |

| 

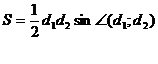
|  
 
|
| ромб | квадрат | трапеция |

| 
| 
|
| Произвольный четырехугольник | круг | |

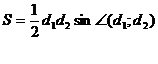
|  
| |
| длина окружности | ||

|
Некоторые теоремы.
Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Обобщенная теорема Фалеса. Если параллельные прямые пересекают две прямые, то они отсекают на них пропорциональные отрезки.
| Теоремы о биссектрисе угла. |
|
| |
| Теоремы о серединном перпендикуляре к отрезку. |
|
|
Окружность.
Определение. Касательная к окружности – это прямая, которая имеет с окружностью одну общую точку.
Свойство касательной. Касательная перпендикулярна к радиусу, проведенному в точку касания.
Признак касательной. Прямая, перпендикулярная к радиусу и проходящая через его конец, лежащий на окружности, является касательной к окружности.
Теорема о пересекающихся хордах. Произведения отрезков пересекающихся хорд равны.
| Теоремы о касательных. |
|
|
Определение. Центральный угол – это угол с вершиной в центре угла.
Определение. Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
| Теоремы об углах между хордами, секущими и касательной. |
|
| |
| |
|
Вписанная окружность.
Определение. Вписанная в многоугольник окружность – это окружность, которая касается всех его сторон.
Теорема 1. В любой треугольник можно вписать окружность. Центр вписанной окружности – точка пересечения биссектрис треугольника.
Теорема 2. (Свойство описанного четырехугольника). Если в четырехугольник вписана окружность, то у него равны суммы противоположных сторон.
Теорема 3. (Признак описанного четырехугольника). Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Описанная окружность.
Определение. Описанная вокруг (около) многоугольник окружность – это окружность, которая проходит через все его вершины.
Теорема 1. Около любого треугольника можно описать окружность. Центр описанной окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Теорема 2. (Свойство вписанного четырехугольника). Если около четырехугольник описана окружность, то у него суммы противоположных углов равны 180о.
Теорема 3. (Признак вписанного четырехугольника). Если суммы противоположных углов выпуклого четырехугольника равны 180о, то в него можно вписать окружность.
Не нашли, что искали? Воспользуйтесь поиском: