РЕАЛЬНАЯ МАТЕМАТИКА

ТЕСТ ГИА - 2013 ПО МАТЕМАТИКЕ.

ВАРИАНТ 1.

(некоторые задания, включенные в данный тест, могут, с определенной степенью вероятности, войти в реальные варианты при проведении ГИА по математике в 2013 году; в любом случае, основу реальных вариантов будут составлять задания именно такого типа (по форме, структуре и сложности), варьируя лишь числовые данные условия; поэтому решение данного теста будет очень полезным при подготовке к государственной итоговой аттестации; задания в тесте согласно новой форме проведения ГИА, сгруппированы в 3 модуля: алгебра, геометрия и реальная математика; готовые решения заданий входящих в тест можно посмотреть перейдя по соответствующим ссылкам)

АЛГЕБРА

ЧАСТЬ 1

1. Найдите значение выражения:

2. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?

Варианты ответа:1) M 2) N 3) P 4) Q

3. Значение какого из выражений является рациональным числом?

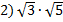
4. Решите уравнение:

5. График какой из приведенных ниже функций изображен на рисунке?

Варианты ответа:1) 2) 3) 4)

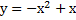
6. На координатной плоскости проведена прямая CD. Укажите уравнение этой прямой.

Варианты ответа: 1) 2) 3) 4)

7. Дана арифметическая прогрессия: 3, 7, 11, Найдите сумму первых пяти её членов.

8. Упростите выражение

и найдите его значение при

9. Решите неравенство:

ЧАСТЬ 2

10. Сократить дробь:

11. Построить график . При каких значениях аргумента функция принимает отрицательные значения?

12. В свежих яблоках 80% воды, а в сушеных – 20%. На сколько процентов уменьшается масса яблок при сушке?

ГЕОМЕТРИЯ

ЧАСТЬ 1

13. Укажите номера верных утверждений.

1) Диагонали параллелограмма равны.

2) Два различных диаметра окружности пересекаются в точке, являющейся центром.

3) Сумма углов трапеции равна

4) Площадь прямоугольного треугольника равна произведению катетов.

5) Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.

14. В треугольнике АВС угол С равен , а угол А равен , . Найдите высоту СН.

15. Один острый угол прямоугольного треугольника на 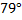больше другого. Найдите больший острый угол. Ответ дайте в градусах.

16. Найдите диагональ квадрата, если его площадь равна 98.

17. В треугольнике АВС угол С равен , . Найдите

18. Вектор с началом в точке А(3;2) имеет координаты (- 6; 6). Найдите абсциссу точки В.

ЧАСТЬ 2

19. Докажите, что площадь параллелограмма равна произведению его основания на высоту.

20. В прямоугольном треугольнике АВС из вершины прямого угла С проведены биссектриса CL и медиана CM. Найдите площадь треугольника АВС, если LM = a, CM = b.

РЕАЛЬНАЯ МАТЕМАТИКА

21. В таблице приведены нормативы по бегу на 30 метров для 9 класса.

Оцените результат девочки, пробежавшей эту дистанцию за 5,63 с.

1) Отметка «5» 2) Отметка «4» 3) Отметка «3» 4) Норматив не выполнен.

22. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим значением температуры и наименьшим. Ответ дайте в градусах Цельсия.

23. На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина 31 руб. 20 коп. Сдачи клиент получил 1 руб. 60 коп. Сколько литров бензина было залито в бак?

24. Сколь всего осей симметрии имеет фигура, изображённая на рисунке?

25. Проектор полностью освещает экран А высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 160 см, чтобы он был полностью совещён, если настройки проектора остаются неизменными?

26. Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме. Сколько примерно учащихся получили положительную отметку «3», «4» или «5», если всего в школе 120 девятиклассников?

Варианты ответа:1) более 100 учащихся 2) около 70 учащихся

3) около 90 учащихся 4) менее 60 учащихся

27. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

28. Расстояние s (в метрах) до места удара молнии можно приближенно вычислить по формуле , 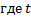– количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если . Ответ дайте в километрах, округлив его до целых.

Полезная информация:

Демонстрационный вариант КИМ ГИА - 2013 по математике

Справочные материалы разрешенные к использованию при сдаче ГИА - 2013 по математике

Литература для подготовки к ГИА:

Алгебра

Часть 2

21. Решите систему уравнений {y-5x=-8

y-x2=-2 (х в квадрате)
22. Расстояние между городами А и В равно 375 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 1 час 30 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С.
23. Постройте график функции y= x-2/(x2-2x)2 и найдите все значения k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.

24. Основания равнобедренной трапеции равны 8 и 18, а ее периметр равен 52. Найдите площадь трапеции.
25. На стороне AC треугольника ABC отмечены точки D и E так, что AD=CE. Докажите, что если BD=BE, то AB=BC
26. Окружность радиуса 4 касается внешним образом второй окружности в точке B. Общая касательная к этим окружностям, проходящая через точку B, пересекается с некоторой другой их общей касательной в точке A. Найдите радиус второй окружности, если AB=6

Теоремы и общие сведения по геометрии.

1) Два угла называются смежными, если у них одна сторона общая, а две другие стороны этих углов являются дополнительными полупрямыми.
2) Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
3) Сумма смежных углов равна 180°.
4) Вертикальные углы равны.

5) Угол, равный 90°, называется прямым углом. Прямые, пересекающиеся под прямым углом, называются перпендикулярными.
6) Через каждую точку прямой можно провести и притом только одну, перпендикулярную прямую.
7) Угол, меньший 90°, называется острым. Угол больший 90°, называется тупым.
8) Признаки равенства треугольников.
- по двум сторонам и углу между ними;
- по стороне и двум прилегающим к ней углам;
- по трем сторонам.
9) Треугольник называют равнобедренным, если у него две стороны равны.
10) Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

11) Биссектрисой треугольника называют отрезок прямой, заключенной между вершиной и точкой ее пересечения с противоположной стороной, которая делит угол пополам.
12) Высота треугольника – это отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону, или на ее продолжение.
13) Треугольник называется прямоугольным, если у него есть прямой угол. В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой. Остальные две стороны, называются катетами.
14) Свойства сторон и углов прямоугольного треугольника:
- углы, противолежащие катетам – острые;
- гипотенуза больше любого из катетов;
- сумма катетов больше гипотенузы.
15) Признаки равенства прямоугольных треугольников:
- по катету и острому углу;
- по двум катетам;
- по гипотенузе и катету;
- по гипотенузе и острому углу.
16) Свойства равнобедренного треугольника:
- в равнобедренном треугольнике углы при основании равны;
- если в треугольнике два угла равны, то он равнобедренный;
- в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;
- если в треугольнике медиана и биссектриса (или высота и биссектриса, или медиана и высота), проведенная из какой-либо вершины, совпадают, то такой треугольник равнобедренный.
17) В треугольнике против большей стороны лежит больший угол, против большего угла лежит большая сторона.

18) (Неравенство треугольника). У каждого треугольника сумма двух сторон больше третьей стороны.
19) Внешним углом треугольника ABC при вершине A называется угол, смежный углу треугольника при вершине A.
20) Сумма внутренних углов треугольника:
- сумма любых двух углов треугольника меньше 180°;
- в каждом треугольнике два угла острые;
- внешний угол треугольника больше любого внутреннего угла, не смежного с ним;
- сумма углов треугольника равна 180°;
- внешний угол треугольника равен сумме двух других углов, не смежных с ним.
- сумма острых углов прямоугольного треугольника равна 90°.
21) Отрезок, соединяющий середины боковых сторон треугольника называется средней линией треугольника.
22) Средняя линия треугольника обладает свойством – она параллельна основанию треугольника и равна ее половине.

23) Длина ломаной не меньше длины отрезка, соединяющей ее концы.
24) Свойства серединного перпендикуляра отрезка:
- точка лежащая на серединном перпендикуляре одинаково удалена от концов отрезка;
- любая точка, одинаково удаленная от концов отрезка, лежит на серединном перпендикуляре.

25) Существование окружности, описанной около треугольника:

- все три серединные перпендикуляры треугольника пересекаются в одной точке и эта точка является центром описанной окружности. Описанная около треугольника окружность всегда существует и она единственна;

- центром описанной окружности прямоугольного треугольника является середина гипотенузы.

26) Существование вписанной в треугольник окружности:

- - все три биссектрисы треугольника пересекаются в одной точке и эта точка является центром вписанной окружности. Вписанная в треугольник окружность всегда существует и она единственна.

27) Признаки параллельности прямых. Теоремы о параллельности и перпендикулярности прямых:

- две прямые, параллельные третьей - параллельны;

- если при пересечении двух прямых третьей, внутренние (внешние) накрест лежащие углы равны, или внутренние (внешние) односторонние углы в сумме равны 180°, то эти прямые параллельны;

- если параллельные прямые пересечены третьей прямой, то внутренние и внешние накрест лежащие углы равны, и внутренние и внешние односторонние углы в сумме равны 180°;

- две прямые, перпендикулярные одной и той же прямой – параллельны;

- прямая, перпендикулярная одной из двух параллельных прямых, перпендикулярна и второй.

28)Окружность – множество всех точек плоскости, равноудаленных от одной точки.

29) Хорда – отрезок, соединяющий две точки окружности.

30)Диаметр – хорда, проходящая через центр.

31)Касательная – прямая, имеющая с окружностью одну общую точку.

32)Центральный угол – угол с вершиной в центре окружности.

33)Вписанный угол – угол с вершиной на окружности, стороны которого пересекают окружность.

34) Теоремы, относящиеся к окружности:

- радиус, проведенный в точку касания, перпендикулярен касательной;

- диаметр, проходящий через середину хорды, перпендикулярен ей;

- квадрат длины касательной равен произведению длины секущей на ее внешнюю часть;

- центральный угол измеряется градусной мерой дуги, на которую он опирается;

- вписанный угол измеряется половиной дуги, на которую он опирается, или дополняет его половину до 180°;

- касательные, проведенные к окружности из одной точки, равны;

- произведение секущей на ее внешнюю часть – величина постоянная;

35)Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

36) Признаки параллелограмма. Свойства параллелограмма:

- противоположные стороны равны;

- противоположные углы равны;

- диагонали параллелограмма делятся точкой пересечения пополам;

- сумма квадратов диагоналей равна сумме квадратов всех его сторон;

- если в выпуклом четырехугольнике противоположные стороны равны, то такой четырехугольник – параллелограмм;

- если в выпуклом четырехугольнике противоположные углы равны, то такой четырехугольник – параллелограмм;

- если в выпуклом четырехугольнике диагонали делятся точкой пересечения пополам, то такой четырехугольник – параллелограмм;

- середины сторон любого четырехугольника являются вершинами параллелограмма.

37)Параллелограмм, все стороны которого равны, называется ромбом.

38) Дополнительные свойства и признаки ромба:

- диагонали ромба взаимно перпендикулярны;

- диагонали ромба являются биссектрисами его внутренних углов;
- если диагонали параллелограмма взаимно перпендикулярны, или являются биссектрисами соответствующих углов, то этот параллелограмм – ромб.

39)Параллелограмм, все углы которого прямые, называется прямоугольником.
40) Дополнительные свойства и признаки прямоугольника:

- диагонали прямоугольника равны;

- если диагонали параллелограмма равны, то такой параллелограмм – прямоугольник;

- середины сторон прямоугольника – вершины ромба;

- середины сторон ромба – вершины прямоугольника.

41)Прямоугольник, у которого все стороны равны, называется квадратом.

42) Дополнительные свойства и признаки квадрата:

- диагонали квадрата равны и перпендикулярны;

- если диагонали четырехугольника равны и перпендикулярны, то такой четырехугольник – квадрат.

43)Четырехугольник, две стороны которого параллельны, называется трапецией.

44)Отрезок, соединяющий середины боковых сторон трапеции называется средней линией трапеции.

45) Свойства трапеции:

- в равнобокой трапеции углы при основании равны;

- отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований трапеции.

46) Средняя линия трапеции обладает свойством – она параллельна основаниям трапеции и равна их полусумме.

47) Признаки подобия треугольников:

- по двум углам;

- по двум пропорциональным сторонам и углу между ними;

- по трем пропорциональным сторонам.

48) Признаки подобия прямоугольных треугольников:

- по острому углу;

- по пропорциональным катетам;

- по пропорциональным катету и гипотенузе.

49) Соотношения в многоугольниках:

- все правильные многоугольники подобны друг другу;

- сумма углов любого выпуклого многоугольника равна 180°(n-2);

- сумма внешних углов любого выпуклого многоугольника, взятых по одному у каждой вершины, равна 360°.

- периметры подобных многоугольников относятся, как их сходственные стороны, и это отношение равно коэффициенту подобия;

- площади подобных многоугольников относятся, как квадраты их сходственных сторон, и это отношение равно квадрату коэффициента подобия;

Не нашли, что искали? Воспользуйтесь поиском: