
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Подобие треугольников.
Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия:
v два угла одного треугольника равны двум углам другого треугольника;
v две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны;
v три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.
 |
Замечательные линии и точки в треугольнике.
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника.Ортоцентр остроугольного треугольника (точка O, рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (точка O, рис.27) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

 |
Три медианы треугольника (AD, BE, CF, рис.28) пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
 |
Три биссектрисы треугольника (AD, BE, CF, рис.29) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанной окружности.
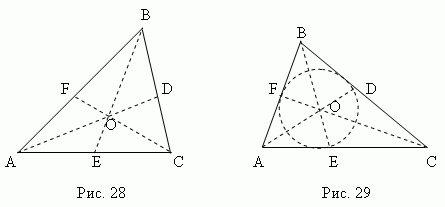
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам; например, на рис.29 AE: CE = AB: BC.
 |
Три срединных перпендикуляра треугольника АВС (KO, MO, NO, рис.30) пересекаются в одной точке О, являющейся центром описанной окружности (точки K, M, N – середины сторон треугольника ABC).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанной и центр вписанной окружности совпадают только в равностороннем треугольнике.
Не нашли, что искали? Воспользуйтесь поиском: