Другий закон (друге начало) термодинаміки: в ізольованій системі неможливий перехід теплоти від менш нагрітого тіла до більш нагрітого.

Це формулювання 2-го закону термодинаміки належить німецькому фізику Клаузіусу, який в 1865 р. ввів у науку фундаментальне поняття ентропії. Ентропія - це така функція стану, що характеризує напрямок самодовіль-ного процесу в ізольованій системі. Ентропія ізольованої системи зростає з наближенням до рівноважного стану. У рівновазі ентропія досягає свого максимального значення.

Важлива роль, яка відводиться в термодинаміці ентро­пії, пов'язана принаймні з двома причинами:

1) зміна ентропії характеризує теплоту 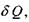яку одержала або віддала система при взаємодії з оточенням: (знак "=" відповідає зворотним процесам, тоді як знак ">" - незворотним, реальним процесам в природі);

2) ентропія характеризує ступінь впорядкованості (або невпорядкованості) системи. Згідно з принципом Больцмана ентропія пов'язана з термодинамічною ймовірністю ста­ну системи за допомогою такого фундаментального спів­відношення:

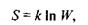(5.2)

де - стала Больцмана. Не входячи в теоретичні тонкощі, можна стверджувати, що термодинамічна ймовірність дорівнює числу мікростанів, за допомогою яких реалізується даний емпіричний стан системи при заданій енергії, об'ємі та кількості частинок.

Термодинамічні потенціали. Термодинамічний стан будь-якої системи повністю визначається її термодинаміч­ними потенціалами. Для кожного повного набору неза­лежних термодинамічних параметрів існує певний термоди­намічний потенціал, за допомогою якого можуть бути обчислені будь-які макроскопічні характеристики системи. Наведемо визначення і основні властивості чотирьох термо­динамічних потенціалів - внутрішньої енергії, ентропії, вільної енергії Гіббса і вільної енергії Гельмгольця.

Внутрішня енергія Перші два закони (начала) термодинаміки дають спільно такий вираз для зміни внутрішньої енергії відкритої однокомпонентної системи:

(5.3)

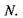З цього співвідношення випливає, що внутрішня енергія є природним термодинамічним потенціалом при обранні в якості набору незалежних змінних ентропії об'єму і кількості часток Диференціювання внутрішньої енергії дає такі параметри, як температура тиск і хімічний потенціал що є спряженими в термодинамічному сенсі обраному набору незалежних змінних:

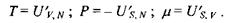
Очевидно, що зміна внутрішньої енергії при адіабатич­ному процесі визначається роботою діючих на систему зовнішніх сил, тоді як в умовах постійності об'єму ця зміна визначається теплотою, що передається системі.

Ентропія (тепловміст) Ентропія пов'язана з внутрішньою енергією таким співвідношенням:

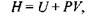
а її повний диференціал

(5.4)

З цього виразу стає зрозуміло, що ентропія, як термодинамічний потенціал, має бути використана для набору незалежних змінних Для ізобаричного процесу зміна ентропії визначається теплотою, що поглинає (віддає) система. Диференціювання ентропії дає параметри:

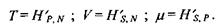
Вільна енергія Гіббса Вільна енергія Гіббса пов'я­зана такими співвідношеннями з внутрішньою енергією і ентропією:

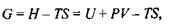
а її повний диференціал

(5.5)

Видно, що вільній енергії Гіббса відповідає набір незалежних змінних Спряжені в термодинамічному значенні параметри виходять як такі похідні від вільної енергії Гіббса:

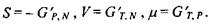
Останнє співвідношення показує, що хімічний потенці­ал є вільна енергія Гіббса в розрахунку на один моль при сталих температурі та тиску. У зв'язку з проведеним у попередньому шостому розділі розглядом мембранних електричних потенціалів клітин зауважимо, що в присут­ності електричного поля та із врахуванням розчиненої речовини хімічний потенціал (в цьому випадку його називають електрохімічним потенціалом) має такий вигляд:

(в розрахунку на одну молекулу);

(в розрахунку на один моль),

де - валентність; - елементарний заряд; - число Фара­дея; - хімічний потенціал розчинника; - концентрація розчиненої речовини (наприклад, певного іона); - потен­ціал електричного поля.

Вільна енергія Гельмгольця Для цього термодина­мічного потенціалу маємо:

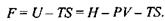
Відповідно

(5.6)

Звідси випливає, що для вільної енергії Гельмгольця природним набором незалежних змінних є Необхідно відзначити також, що в природних умовах значно легше реалізувати вимогу постійності температури ніж ентропії Тому два останніх термодинамічних потенціали - вільні енергії Гіббса і Гельмгольця - знаходять більш широке застосування для опису медико-біологічних систем, оскільки для них ізотермічно-ізобарні або ізотермічно-ізохорні умови є найбільш природними. З наближенням до положення рівноваги вільні енергії Гіббса і Гельмгольця набувають своїх мінімальних значень.

Не нашли, что искали? Воспользуйтесь поиском: