
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задача о назначениях
В общем случае в данной задаче необходимо распределить среди работников работы таким образом, чтобы суммарные затраты на их выполнение были минимальными.
Пусть имеется n работ и n претендентов на их выполнение, которые могут выполнять любую из имеющихся работ. Известны затраты (производительность) ci,j (qi,j) на выполнение i-м работником j-й работы. Цель задачи – найти оптимальное распределение (с минимальными суммарными затратами или максимальной суммарной производительностью) работ среди работников.
Задачу о назначениях n работников на n работ удобно представлять в виде таблицы.
| Работы | ||||||
| …. | n | |||||
| Работники | с1,1 | с1,2 | .... | .... | с1,n | |
| с2,1 | с2,2 | …. | .... | с2,n | ||
| …. | …. | …. | .... | …. | ||
| .... | …. | …. | …. | .... | …. | |
| n | сn,1 | сn,1 | …. | .... | сn,n |
Данная задача имеет следующие ограничения:
- количество работ должно равняться количеству претендентов (равенство можно достичь введением в модель либо фиктивной работы, либо фиктивного работника);
- каждый работник должен быть назначен только на одну работу;
- на каждую работу следует назначить только одного претендента.
Построим математическую модель задачи.
Введем переменные хi,j:
 1, если i-й работник назначен на j-ю работу,
1, если i-й работник назначен на j-ю работу,
хi,j =
0, если i-й работник не назначается на j-ю работу.
Требуется минимизировать (максимизировать) выражение

при соблюдении условий
 , i = 1, 2, …, n;
, i = 1, 2, …, n;
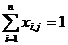 , j = 1, 2,..., n.
, j = 1, 2,..., n.
Данные условия означают, что каждый претендент назначается только на одну работу, а на каждую работу назначается только один работник. Таким образом, матрица X = (хi,j) назначений – допустимое решение задачи – содержит в каждом столбце и в каждой строке ровно по одной единице, все остальные элементы матрицы – нули.
Задача о назначениях является частным случаем транспортной задачи. Эффективным методом решения задачи о назначениях является венгерский метод.
Не нашли, что искали? Воспользуйтесь поиском: