
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод ветвей и границ
Метод ветвей и границ относится к комбинаторным оптимизационным методам. Он предполагает направленный перебор вариантов и в ряде случае позволяет уйти от полного перебора. Метод основан на разбиении всего множества решений задачи на подмножества (ветвление) и оценивании стоимости решения на каждом подмножестве.
Рассмотрим общую идею и алгоритм решения задачи коммивояжера методом ветвей и границ с помощью алгоритма Литтла.
Пусть W – множество всех замкнутых маршрутов, проходящих через все города по одному разу. Такие маршруты называют гамильтоновыми контурами. Для каждого маршрута известна его длина. Основная идея метода состоит в том, что вначале находят нижнюю границу длин всех гамильтоновых контуров W0, т.е. число, не большее, чем длина любого гамильтонова контура (нижняя оценка длины маршрута). Это число может быть найдено до того, как найден сам наиболее короткий маршрут.
Далее все множество гамильтоновых контуров разбивается на два подмножества таким образом, чтобы любой контур в первом множестве  содержал некоторую дугу (i, j), т.е. переход из города i в город j; второе множество
содержал некоторую дугу (i, j), т.е. переход из города i в город j; второе множество  состоит из контуров, эту дугу не содержащих. Для каждого из этих подмножеств определяются нижние границы длины входящих в них гамильтоновых контуров (нижняя оценка длины маршрута) аналогично тому, как это определялось для всего множества. Для дальнейшего рассмотрения выбирается подмножество с меньшей оценкой. Это подмножество в свою очередь подвергается ветвлению на два, для каждого из которых определяется нижняя оценка длины маршрута. Из всех не исследованных к данному моменту подмножеств (т. е. таких, которые еще не были подвергнуты разбиению, или ветвлению) для дальнейшего рассмотрения выбирается подмножество с меньшей оценкой и т. д. пока не будет определен гамильтонов контур минимальной длины. Параллельно расчетам строится дерево ветвления.
состоит из контуров, эту дугу не содержащих. Для каждого из этих подмножеств определяются нижние границы длины входящих в них гамильтоновых контуров (нижняя оценка длины маршрута) аналогично тому, как это определялось для всего множества. Для дальнейшего рассмотрения выбирается подмножество с меньшей оценкой. Это подмножество в свою очередь подвергается ветвлению на два, для каждого из которых определяется нижняя оценка длины маршрута. Из всех не исследованных к данному моменту подмножеств (т. е. таких, которые еще не были подвергнуты разбиению, или ветвлению) для дальнейшего рассмотрения выбирается подмножество с меньшей оценкой и т. д. пока не будет определен гамильтонов контур минимальной длины. Параллельно расчетам строится дерево ветвления.
Рассмотрим основные шаги решения.
1 шаг. Осуществить приведение матрицы по строкам: определить минимальный элемент каждой строки и вычесть из элементов строк найденный минимальный элемент.
2 шаг. Осуществить приведение матрицы по столбцам: определить минимальный элемент в каждом столбце и вычесть из элементов столбцов найденный минимальный элемент.
3 шаг. Найти константу приведения (j0) как сумму найденных минимальных элементов строк и столбцов. Константа приведения j0 является нижней границей длины для множества гамильтоновых контуров.
4 шаг. Для каждого нуля приведенной матрицы определить его «степень» как сумму минимальных элементов строки и столбца, содержащих этот нуль.
5 шаг. Нулевой элемент с наибольшей степенью задает дугу (t0, j0), по которой проводится разбиение множества гамильтоновых контуров (t0 – строка, а j0 – столбец, на пересечении которых находится выбранный нулевой элемент). В множество  включаются все контуры, содержащие эту дугу, в множество
включаются все контуры, содержащие эту дугу, в множество 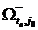 – не содержащие ее.
– не содержащие ее.
6 шаг. Матрицу, описывающую множество  , получаем из приведенной матрицы путем вычеркивания строки to и столбца jo. На дереве ветвления обозначаем, что рассматриваются контуры, включающие дугу (t0, j0). Вводя в маршрут дугу (to, jo), следует заблокировать все изолированные контуры, которые могут содержать эту дугу. Для блокировки в соответствующую клетку матрицы вводится «¥». В частности, значение элемента (jo, to) в матрице заменяем на ¥, так как рассматриваются маршруты, содержащие переход из города t0 в j0, а значит, обратный переход из города jo в to уже невозможен.
, получаем из приведенной матрицы путем вычеркивания строки to и столбца jo. На дереве ветвления обозначаем, что рассматриваются контуры, включающие дугу (t0, j0). Вводя в маршрут дугу (to, jo), следует заблокировать все изолированные контуры, которые могут содержать эту дугу. Для блокировки в соответствующую клетку матрицы вводится «¥». В частности, значение элемента (jo, to) в матрице заменяем на ¥, так как рассматриваются маршруты, содержащие переход из города t0 в j0, а значит, обратный переход из города jo в to уже невозможен.
7 шаг. Выполнить приведение матрицы множества  по строкам и столбцам и определить нижнюю границу этого множества по формуле:
по строкам и столбцам и определить нижнюю границу этого множества по формуле:
 ,
,
где
 – сумма минимальных элементов, используемых для приведения матрицы множества
– сумма минимальных элементов, используемых для приведения матрицы множества  .
.
8 шаг. Матрицу множества  получаем из исходной матрицы, рассматриваемой на шаге 4, заменой элемента (to, jo) на ¥.
получаем из исходной матрицы, рассматриваемой на шаге 4, заменой элемента (to, jo) на ¥.
9 шаг. Для полученной матрицы множества  определить константу приведения (
определить константу приведения ( ) и нижнюю границу множества по формуле
) и нижнюю границу множества по формуле
 ,
,
выполнить приведение матрицы.
10 шаг. Дальнейшему ветвлению подвергается подмножество, имеющее меньшее значение нижней границы.
11 шаг. Для выбранного множества повторить шаги 4–9.
12 шаг. Процесс считается завершенным, когда остается матрица размера 2х2. Для данной матрицы в гамильтонов контур включаются связи, соответствующие нулевым элементам.
13. шаг. Найти длину полученного гамильтонова контура и сравнить ее с оценками (нижними границами) еще не исследованных множеств. Если все нижние границы не исследованных множеств больше или равны длине найденного контура, задача считается решенной. В противном случае следует продолжить ветвление с множества, имеющего наименьшую нижнюю границу.
Задача
Решить методом ветвей и границ задачу коммивояжера со следующей матрицей расстояний (эта же задача решалась в предыдущем параграфе методом ближайшего соседа).
| Города | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
Решение
Осуществим приведение матрицы по строкам, определив минимальное значение в каждой строке (ui).
| Города | ui | ||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ |
Вычтем минимальные элементы из соответствующих строк и определим сумму минимальных значений.
| Города | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
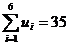
Осуществим приведение матрицы по столбцам, определив минимальное значение в каждом столбце (ni).
| Города | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ni |
Вычтем минимальные элементы из соответствующих столбцов и определим сумму минимальных значений.
| Города | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
 .
.
Константа приведения: 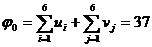
Найдем степени нулей для приведенной матрицы. Для этого выберем минимальные элементы в строке и столбце, где расположен нуль, и просуммируем их.
| Города | ||||||
| ¥ | 2 | 03 | ||||
| ¥ | 02 | |||||
| ¥ | 09 | |||||
| ¥ | 00 | 00 | ||||
| 05 | 02 | ¥ | ||||
| 07 | ¥ |
Наибольшая степень нулевого элемента равна девяти и соответствует связи (3,5). Разобьем множество гамильтоновых контуров на два подмножества  и
и 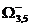 .
.
Матрицу множества  получаем вычеркиванием третьей строки и пятого столбца приведенной матрицы. Элемент (5,3) заменим на ¥.
получаем вычеркиванием третьей строки и пятого столбца приведенной матрицы. Элемент (5,3) заменим на ¥.
| Города | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
Сделаем приведение полученной матрицы по третьему столбцу (нет нулевого элемента) и определим нижнюю границу множества.
| Города | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
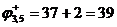
Матрицу множества 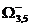 получим путем замены элемента (3,5) на ¥.
получим путем замены элемента (3,5) на ¥.
| Города | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ¥ | |||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
Осуществим приведение матрицы по третьей строке (нет нулевого элемента) и определим нижнюю границу множества.
| Города | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ¥ | |||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
 .
.
Отобразим проделанные действия на дереве ветвления.


 W0 j0 = 37
W0 j0 = 37


 (3,5)
(3,5) 

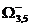
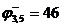
Для дальнейшего исследования выбираем множество  , т. к. ему соответствует меньшая нижняя граница:
, т. к. ему соответствует меньшая нижняя граница:  <
<  . Множество
. Множество  подвергаем дальнейшему ветвлению
подвергаем дальнейшему ветвлению
Находим степени нулей матрицы множества  .
.
| Города | |||||
| ¥ | 00 | 02 | |||
| ¥ | 00 | 00 | |||
| 00 | ¥ | 00 | |||
| 010 | ¥ | ||||
| 06 | ¥ |
Ячейка (5,1) содержит наибольшую степень нуля. Разобьем множество  на два подмножества
на два подмножества  и
и  . Матрицу подмножества
. Матрицу подмножества  получаем из матрицы множества
получаем из матрицы множества  вычеркиванием в последней пятой строки и первого столбца. Кроме того, дуги (3,5) и (5,1), введенные в маршрут, могут породить изолированный контур, поэтому в клетку (1,3) поместим ¥.
вычеркиванием в последней пятой строки и первого столбца. Кроме того, дуги (3,5) и (5,1), введенные в маршрут, могут породить изолированный контур, поэтому в клетку (1,3) поместим ¥.
 (3,5)®(5,1)
(3,5)®(5,1)
| Города | ||||
| ¥ | 0 | |||
| ¥ | 0 | 0 | ||
| 0 | ¥ | 0 | ||
| 0 | ¥ |
В данной матрице все строки и столбцы содержат нулевые элементы, поэтому нижняя граница множества остается равной 39:
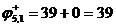
Матрицу подмножества  получаем из матрицы множества
получаем из матрицы множества  заменой значения элемента (5,1) на ¥.
заменой значения элемента (5,1) на ¥.
| Города | |||||
| ¥ | 0 | 0 | |||
| ¥ | 0 | 0 | |||
| 0 | ¥ | 0 | |||
| ¥ | ¥ | ||||
| 0 | ¥ |
Приведем матрицу по первому столбцу (минимальное значение равно 5) и по пятой строке (минимальное значение равно пяти).
| Города | |||||
| ¥ | 0 | 0 | |||
| ¥ | 0 | 0 | |||
| 0 | ¥ | 0 | |||
| ¥ | ¥ | ||||
| 0 | ¥ |
Нижняя граница множества:
 .
.
Сравним нижние границы множеств, еще не подверженных ветвлению. Так как  <
<  <
<  , то дальнейшему ветвлению подвергнем множество
, то дальнейшему ветвлению подвергнем множество  . Обозначим это на дереве ветвления (см. рис. 3.3.1).
. Обозначим это на дереве ветвления (см. рис. 3.3.1).
Определим степени нулей матрицы множества  .
.
| Города | ||||
| ¥ | 02 | |||
| ¥ | 00 | 00 | ||
| 00 | ¥ | 00 | ||
| 06 | ¥ |
Ячейка (6,2) имеет наибольшую степень нуля. Разобьем множество  на два подмножества
на два подмножества  и
и 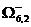 . Константа приведения для матрицы множества
. Константа приведения для матрицы множества  равна нулю.
равна нулю.
| Города | |||
| 0 | 0 | ||
| 0 | ¥ | ||
| 0 | ¥ | 0 |
Нижняя граница множества:
 .
.
Подмножество 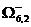 получаем из множества
получаем из множества  заменой значения элемента (6,2) на ¥.
заменой значения элемента (6,2) на ¥.
| Города | ||||
| 0 | 0 | |||
| ¥ | 0 | 0 | ||
| 0 | ¥ | 0 | ||
| ¥ | ¥ |
Сделаем приведение матрицы по столбцу 2 и строке 6. Минимальный элемент равен двум.
| Города | ||||
| 0 | 0 | |||
| ¥ | 0 | 0 | ||
| 0 | ¥ | 0 | ||
| ¥ | ¥ |
Нижняя граница множества равна 45:
 .
.
Из всех множеств, еще не подвергнутых ветвлению (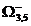 ,
,  ,
,  ,
,  ) выбираем
) выбираем  как имеющее наименьшую нижнюю границу (см. рис. 3.3.1).
как имеющее наименьшую нижнюю границу (см. рис. 3.3.1).
Находим степени нулей матрицы множества  .
.
| Города | |||
| 00 | 02 | ||
| 02 | ¥ | ||
| 00 | ¥ | 03 |
Ячейка (4,6) содержит наибольшую степень нуля. Разобьем множество  на два подмножества
на два подмножества  и
и  . Множество
. Множество  получим вычеркиванием четвертой строки и шестого столбца множества
получим вычеркиванием четвертой строки и шестого столбца множества  . Для удаления изолированного контура
. Для удаления изолированного контура
 (4,6)®(6,2)
(4,6)®(6,2)
введем ¥ в клетку (2,4).
| Города | ||
| 0 | 0 | |
| 0 | ¥ |
Константа приведения данной матрицы равна нулю. Нижняя граница множества равна:
 .
.
Множество  получим из множества
получим из множества  заменой значения элемента (4,6) на ¥.
заменой значения элемента (4,6) на ¥.
| Города | |||
| 0 | 0 | ||
| 0 | ¥ | ||
| 0 | ¥ | ¥ |
Приведение матрицы проведем по шестому столбцу. Минимальный элемент равен трем.
| Города | |||
| 0 | 0 | ||
| 0 | ¥ | ||
| 0 | ¥ | ¥ |
Нижняя граница множества равна:
 .
.
Множество  имеет наименьшую нижнюю границу из всех еще не рассмотренных множеств. Поэтому подвергаем множество
имеет наименьшую нижнюю границу из всех еще не рассмотренных множеств. Поэтому подвергаем множество  дальнейшему исследованию. Матрица множество
дальнейшему исследованию. Матрица множество  имеет размерность 2х2. В гамильтонов контур включим связи (1,4) и (2,3).
имеет размерность 2х2. В гамильтонов контур включим связи (1,4) и (2,3).
Таким образом, в полученный гамильтонов контур Г входят связи (3,5), (5,1), (6,2), (4,6), (1,4), (2,3), после их упорядочивания получаем маршрут: 3 – 5 – 1 – 4 - 6 – 2 – 3. Полное дерево ветвлений представлено на рисунке (рис. 3.3.1).
Длина гамильтонова контура:
Z = 3 – 5 – 1 – 4 - 6 – 2 - 3 = 4 + 7 + 8 + 10 + 3 + 7 = 39 км.
Так как нижняя граница оборванных множеств больше полученного значения, следовательно, найденный контур дает оптимальное решение.

W0 j0 = 37
(3,5) 

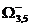
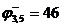
(5,1) 
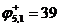

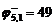
(6,2) 

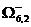
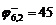
(4,6) 


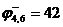
Рис. 3.3.1. Дерево решений.
Задачи
Транспортная задача
| 1. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 2. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
| 3. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом Фогеля. | ||||||
| 4. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 5. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
| 6. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом Фогеля. | ||||||
| 7. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 8. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
| 9. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом Фогеля. | ||||||
| 10. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 11. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
| 12. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом Фогеля. | ||||||
| 13. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 14. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
| 15. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом Фогеля. | ||||||
| 16. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 17. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
| 18. Решить транспортную задачу распределительным методом. Начальное решение Х0 найти методом Фогеля. | ||||||
| 19. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом северо-западного угла. | ||||||
| 20. Решить транспортную задачу методом потенциалов. Начальное решение Х0 найти методом наименьшей стоимости. | ||||||
Задачи о назначениях и коммивояжера
(при решении задачи коммивояжера замените все элементы главной диагонали матрицы расстояний на ∞)
| 1. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| 2. а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| 3. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ветвей и границ. | ||||||
| 4. а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ветвей и границ. | ||||||
| 5. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| 6. а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| 7. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ветвей и границ. | ||||||
| 8. а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ветвей и границ. | ||||||
| 9. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| 11. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ветвей и границ. | ||||||
| 12. а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ветвей и границ. | ||||||
| 13. а) Решить задачу о назначениях с помощью венгерского алгоритма на максимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
| 14. а) Решить задачу о назначениях с помощью венгерского алгоритма на минимум. б) Решить задачу коммивояжера методом ближайшего соседа. | ||||||
Не нашли, что искали? Воспользуйтесь поиском: