
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 2 Уравнения электростатики. Прямая и обратная задачи электростатики, 6ч.
Задачи 2.1, 2.2, 2.4, 2.7 [1]
2.1. Бесконечно тонкая плоская плита равномерно заряжена по поверхности. Найти потенциал  и напряженность электрического поля
и напряженность электрического поля  .
.
2.2. Плотность заряда слоистой среды описывается функцией  . Разбив распределение заряда на тонкие слои, выразить через
. Разбив распределение заряда на тонкие слои, выразить через  потенциал
потенциал  и напряженность электрического поля
и напряженность электрического поля  (построить функцию Грина одномерного уравнения Лапласа).
(построить функцию Грина одномерного уравнения Лапласа).
2.3. Плоская бесконечная плита толщины 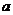 заряжена по объему с плотностью
заряжена по объему с плотностью  : а).
: а). 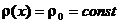 , б).
, б). 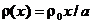 , в)
, в)  . Провести расчет потенциала
. Провести расчет потенциала  и напряженности электрического поля
и напряженности электрического поля  . Проанализировать зависимости потенциала и напряженности электрического поля от расстояния до центра плиты для всех выше указанных случаев.
. Проанализировать зависимости потенциала и напряженности электрического поля от расстояния до центра плиты для всех выше указанных случаев.
2.4. Найти потенциал и напряженность поля, создаваемого системой зарядов, расположенных на плоскости. Поверхностная плотность зарядов  .
.
2.5. Плоскость 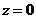 заряжена с плотностью, которая изменяется по периодическому закону
заряжена с плотностью, которая изменяется по периодическому закону 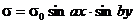 , образуя бесконечную поверхностную решетку. Найти потенциал этой системы зарядов.
, образуя бесконечную поверхностную решетку. Найти потенциал этой системы зарядов.
2.6. Заряд распределен в пространстве по периодическому закону 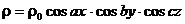 , образуя бесконечную пространственную периодическую решетку. Найти потенциал электрического поля.
, образуя бесконечную пространственную периодическую решетку. Найти потенциал электрического поля.
2.7. Бесконечно длинный круговой цилиндр радиуса 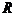 равномерно заряжен по поверхности так, что на единицу его длины приходиться заряд
равномерно заряжен по поверхности так, что на единицу его длины приходиться заряд  . Найти потенциал
. Найти потенциал  и напряженность электрического поля
и напряженность электрического поля  .
.
2.8. Найти потенциал  и напряженность электрического поля
и напряженность электрического поля  равномерно заряженной прямолинейной бесконечной нити (построить функцию Грина двумерного уравнения Лапласа).
равномерно заряженной прямолинейной бесконечной нити (построить функцию Грина двумерного уравнения Лапласа).
2.9. Определить распределение электрического поля, создаваемого заряженной бесконечной нитью, ориентированной вдоль оси 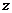 . Плотность заряда распределена вдоль нити по закону:
. Плотность заряда распределена вдоль нити по закону: 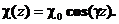
2.10.* Заряд распределен равномерно по поверхности прямолинейной, бесконечно длинной полосы с шириной 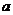 . Используя явное выражение для функции Грина двумерного уравнения Лапласа, найти потенциал
. Используя явное выражение для функции Грина двумерного уравнения Лапласа, найти потенциал  и напряженность электрического поля
и напряженность электрического поля  .
.
2.11.* Заряд распределен цилиндрически симметричным образом:  (
( ). Разбив распределение заряда на тонкие цилиндрические слои, выразить через
). Разбив распределение заряда на тонкие цилиндрические слои, выразить через 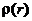 потенциал
потенциал  и напряженность электрического поля
и напряженность электрического поля  (построить функцию Грина двухмерного уравнения Лапласа).
(построить функцию Грина двухмерного уравнения Лапласа).
2.12.* Найти потенциал  и напряженность электрического поля
и напряженность электрического поля  , создаваемого сферой радиуса
, создаваемого сферой радиуса 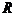 , равномерно заряженной по поверхности. Полный заряд сферы равен
, равномерно заряженной по поверхности. Полный заряд сферы равен 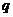 .
.
2.13.* Заряд распределен сферически симметричным образом:  . Разбив распределение заряда на тонкие сферические слои, выразить через
. Разбив распределение заряда на тонкие сферические слои, выразить через 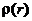 потенциал
потенциал  и напряженность электрического поля
и напряженность электрического поля  (построить функцию Грина трехмерного уравнения Лапласа для сферически симметричной системы).
(построить функцию Грина трехмерного уравнения Лапласа для сферически симметричной системы).
2.14.* Определить напряженность электрического поля внутри и снаружи шара радиуса 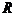 , объемная плотность которого меняется по закону
, объемная плотность которого меняется по закону 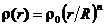 , где
, где 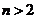 .
.
2.15.* Сфера радиуса  заряжена по поверхности по закону
заряжена по поверхности по закону 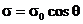 . Найти потенциал
. Найти потенциал  электрического поля.
электрического поля.
Не нашли, что искали? Воспользуйтесь поиском: