Решение уравнений Максвелла; потенциалы и волновое уравнение

Получим из уравнений Максвелла уравнения для потенциалов.

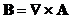
Рассмотрим закон Фарадея:

Вектор, ротор которого равен 0, является градиентом скалярного поля. Обозначим это поле так же, как и электростатический потенциал, в который он превращается, если ничто не меняется во времени:

Преобразуем последнее уравнение Максвелла:

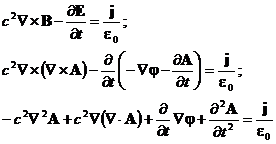
Используем свободу в выборе дивергенции А, выбирая:

(калибровка Лоренца)

Это сильно упрощает уравнения:

Уравнения хорошо разделились - с плотностью заряда стоит j, а с током стоит А.

Можно раскрыть лапласиан:

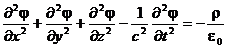
Уравнение имеет симметрию по времени и координатам.

Определив из уравнений потенциалы, можно найти поля:

Мы пришли к уравнениям для потенциалов, которые во многих случаях удобнее.

Если плотность заряда равна 0, то получаем волновое уравнение для потенциала. Например, для одномерного случая:

Решение этого уравнения - волна, которая распространяется со скоростью с.

Не нашли, что искали? Воспользуйтесь поиском: