Волны в пустом пространстве; плоские волны

Уравнения Максвелла для случая отсутствия токов и зарядов, т.е. в пустом пространстве:

Рассмотрим одномерный случай волны, распространяющейся вдоль оси х. Тогда по оси y и z поля не меняются и производные по этим координатам равны 0.

Из полученных уравнений следует, что проекция электрического поля на ось х равна 0, т.е. Е направлена перпендикулярно направлению распространения волны.

Рассмотрим сначала случай наличия у Е только у -компоненты. Потом можно разобрать случай только z -компоненты и скомбинировать эти два случая для получения общего решения.

Если электрическое поле имеет только y -компоненту, то магнитное поле - только z -компоненту. Таким образом, Е ^ В.

Из всех производных по координатам только

Остается

Таким образом, остается два уравнения:

дифференцируем уравнение по х:

дифференцируем уравнение по t:

Объединяем оба полученных уравнения:

.

Изменяя порядок дифференцирования, получаем аналогичное уравнение для магнитного поля:

Это волновое уравнение для одномерных волн. Одним из возможных его решений является функция Е_y (x, t) = ¦(x - ct) - функция, представляющая собой «жесткое» образование вдоль оси х, которое движется по направлению к положительным х со скоростью (с). Иногда удобно считать, что решение одномерного волнового уравнения является функцией от (t - x / c), однако это одно и то же:

F (t - x / c) = ¦(x - ct)

Общее решение:

Е_y = ¦(x - ct) + g (x + ct) - наложение двух волн, существующих одновременно, распространяющихся в противоположных направлениях.

Мы рассмотрели частный случай электрического поля с одной только у -компонентой. Имеется, конечно, и другое решение для волн, бегущих вдоль оси х, при котором электрическое поле обладает одной лишь z -компонентой.

Так как уравнения Максвелла линейны, общее решение для одномерных волн, распространяющихся в направлении х, есть сумма волн Е_у и Е_z.

Общее решение можно суммировать следующими формулами:

Е = (0, Е_у, Е_z),

E_y = f (x - ct) + g (x + ct),

E_z = F (x - ct) + G (x + ct),

B = (0, B_y, B_z),

cB_z = f (x - ct) - g (x + ct)

cB_y = - F (x - ct) + G (x + ct)

Решения для магнитного поля B_z волны получены из решений для электрического поля и исходных уравнений:

;

.

Аналогично для компоненты B_y.

Простейшее решение волнового уравнения для плоской волны

Простейшими решениями волновых уравнений для магнитного и электрического полей являются:

E_y = E_m cos (w t - kx + a₁)

B_z = B_m cos (w t - kx + a₂)

k - волновое число (k = w/ c). Волновое число показывает, на сколько изменяется фаза волны (аргумент косинуса) на единице длины пути в направлении распространения волны.

Подставляя эти решения в исходные уравнения с производными первого порядка, приведенные ниже, получаем:

k E_m sin (w t - kx + a₁) = w B_m sin (w t - kx + a₂)

w E_m sin (w t - kx + a₁) = c ² k B_m sin (w t - kx + a₂)

Для того чтобы уравнения удовлетворялись, необходимо равенство начальных фаз a₁ и a₂. Это значит, что электрическое и магнитное поле волны меняются синхронно во времени и пространстве.

Исключая из уравнений w и k, получаем соотношение электрического и магнитного полей плоской волны: E = cB.

Моментальная «фотография» распределения полей в пространстве для плоской волны представлена на рисунке.

Трехмерные волны.

К тому, что вектор Е удовлетворяет волновому уравнению можно прийти опираясь непосредственно на уравнения Максвелла. Исходим из уравнения:

Берем ротор от обеих частей уравнения:

В пустом пространстве , а из четвертого уравнения Максвелла видим, что

. Отсюда получаем волновое уравнение для Е:

или

Самое общее решение трехмерного волнового уравнения является суперпозицией всех видов плоских волн, бегущих во всех возможных направлениях.

Сферические волны

Рассмотрим теорию сферических волн - волн, которые соответствуют сферическим поверхностям, расходящихся от некоторого центра.

Пусть имеется функция, зависящая только от радиального расстояния r точки от начала координат, иными словами, сферически симметричная функция y (r), где

- расстояние от начала координат

Нам понадобится выражение для лапласиана y:

Причем необходимо выразить лапласиан через одну переменную r. Через обозначим первую производную y по r, а через - вторую. Сначала найдем производные по х:

Отсюда

Будем искать решения трехмерного волнового уравнения

Подставим выражение для лапласиана и умножим уравнение на r:

Последнее уравнение является одномерным относительно функции r y. Его решение:

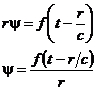
Решение соответствует расходящейся сферической волне, распространяющейся от начала координат со скоростью с. Амплитуда ее убывает обратно пропорционально расстоянию r от начала координат. В начале координат амплитуда волны равна бесконечности. Физически это означает, что в начале координат находится источник волны - движущийся заряд.

Другое возможное решение одномерного волнового уравнения

соответствует сферической волне, бегущей внутрь, от больших r к началу координат. Было бы странно представлять, что прежде, чем заряды были приведены в движение, сферическая волна уже вышла из бесконечности и прибыла к зарядам как раз в тот момент, когда они начали шевелиться. Такое решение возможно, но опыт показывает, что, когда заряды ускоряются, волны распространяются от зарядов, а не к ним. Поэтому физическим смыслом наделяется только расходящаяся волна. При этом, однако, теряется симметрия уравнений Максвелла относительно направления течения времени.

Решения уравнений Максвелла с токами и зарядами.

Сферические волны от точечного источника.

Ранее мы установили, что уравнения Максвелла можно решать подстановкой

где потенциалы обязаны удовлетворять уравнениям

и, кроме того, условию

(калибровка Лоренца)

Будем искать теперь решение волновых уравнений для потенциалов.

Там, где r и j равны нулю (это место называется «пустотой»), потенциалы j и А и поля Е и В удовлетворяют трехмерному волновому уравнению без источников, математическая форма которого такова:

Решения этого уравнения могут представлять волны разных сортов: плоские волны, бегущие в х -направлении y = f (t - x / c); плоские волны, бегущие вдоль у или вдоль z или в любом другом направлении; сферические волны вида

(Решения можно записать иначе - например, в виде цилиндрических волн, разбегающихся от оси).

Физически последняя формула относится не совсем к пустоте: в начале координат должны быть какие-то заряды, иначе расходящаяся волна не получилась бы. Иными словами, формула есть решение волнового уравнения всюду, кроме непосредственной окрестности точки r = 0. Посмотрим, какого рода источник в начале координат способен вызвать расходящуюся сферическую волну. Необходимо решить волновое уравнение с правой частью вида

, где величина s (которая называется источником) известна.

Предположим, что имеется сферическая волна , и поглядим, во что она превращается при очень малых r. Тогда запаздыванием - r / c в

f (t - r / c) можно пренебречь, и поскольку функция f плавная, y превращается в

Итак, y в точности похоже на кулоново поле заряда, расположенного в начале координат. Известно, что для небольшого сгустка заряда, ограниченного очень малой областью близ начала координат и имеющего плотность r,

, где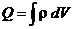

Такой потенциал j удовлетворяет уравнению Пуассона

(Это следует также непосредственно из волнового уравнения). По мере приближения к началу координат зависимость y ~ 1/ r приводит к тому, что пространственные производные y становятся очень большими. Производные y по времени при этом остаются такими же. Так, что можно пренебречь в волновом уравнении множителем по сравнению с )

Следуя тем же расчетам, можем считать

где s связано с f формулами

при этом s, а стало быть, и S может оказаться функцией времени.

Таким образом, решение волнового уравнения с источником имеет вид

Влияние слагаемого с сказывается лишь на появлении запаздывания (t - r / c) в потенциале кулонова типа.

Всякий рассредоточенный источник можно считать состоящим из суммы многих «точечных» источников, расположенных поодиночке в каждом элементе объема dV и имеющих силу s (x,y,z,t) dV. Суммируя их вклад, получим решение волнового уравнения с источниками в виде

Если подразумевать под y скалярный потенциал j, то функция источника s превращается в r/e₀. А можно считать, что y представляет одну из трех компонент векторного потенциала А; тогда s означает соответствующую компоненту j /e₀ c ².

Таким образом, если во всех точках известна плотность зарядов r(х, у, z, t) и плотность тока j (х, у, z, t), то решения уравнений для потенциалов выглядят так:

Решение уравнений Максвелла получено. Общий итог теории Максвелла представлен в рамке.

Уравнения Максвелла: , , 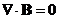, . И их решения:

Электрическое поле, создаваемое отдельным точечным зарядом, который движется произвольным образом.

Из уравнений Максвелла путем громоздких преобразований можно получить выражение для электрического поля, создаваемого отдельным точечным зарядом, который движется произвольным образом:

Если заряд движется произвольным образом, то электрическое поле, которое существует в некоторой точке, в настоящий момент зависит только от положения и движения заряда в более ранний момент времени, отстающий на интервал, необходимый для того, чтобы свет, двигаясь со скоростью с, прошел расстояние от заряда до точки поля. Иными словами, если нужно знать электрическое поле в точке (1) в момент t, то необходимо подсчитать положение 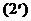заряда и его движение в момент [где - расстояние до точки (1)] из положения заряда 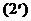в момент . Штрихи здесь напоминают, что - это так называемое «запаздывающее расстояние» от точки 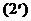к точке (1), а вовсе не теперешнее расстояние между точкой (2) - положением заряда в момент t - и точкой поля (1) (рисунок). Вектор - это единичный вектор, направленный от запаздывающей точки 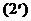к точке (1).

Если бы заряд в своем «запаздывающем» положении создавал кулоново поле, - первое слагаемое можно назвать «запаздывающим кулоновым полем». Электрическое поле обратно пропорционально квадрату расстояния и направлено от «запаздывающего» положения заряда (т.е. по вектору ).

Второе слагаемое показывает, что к запаздывающему кулонову полю надо сделать «поправку», равную быстроте изменения запаздывающего кулонова поля, умноженной на , т.е. на само запаздывание. Два первых слагаемых соответствуют вычислению «запаздывающего кулонова поля» и затем экстраполяции его в будущее, на время , т.е. как раз к моменту t. Экстраполяция линейна, как если предположить, что «запаздывающее кулоново поле» будет по-прежнему изменяться со скоростью, расчитанной для заряда в точке 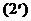. Если поле меняется медленно, эффект запаздывания почти полностью сводится на нет поправочным слагаемым, и оба слагаемых вместе приводят к величине электрического поля, очень близкой к «мгновенному кулонову полю» заряда, находящегося в точке (2).

Имеется еще третье слагаемое - вторая производная единичного вектора . Вдали от заряда два первых слагаемых убывают как обратный квадрат расстояния и на больших расстояниях оказываются слишком слабыми по сравнению с третьим, которое убывает как 1/ r. Рассмотрим его подробнее.

Удобнее рассматривать движущийся заряд из точки, где изучается его действие и направить в противоположную сторону, от точки (1) к .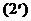

Если скорость заряда v всегда много меньше скорости света (нерелятивистский случай) и если рассматриваются только точки, сильно удаленные от заряда, так что существенным является только третье слагаемое, то поля можно записать в виде

×[проекция ускорения заряда в момент на направление, поперечное к ]

Пусть, например, боковое смещение заряда описывается функцией x (t) и расстояние от заряда r мало меняется от времени. Тогда единичный вектор повернется на угол, приблизительно равный x / r. В этом случае

, где - «запаздывающее» ускорение заряда, взятое в момент времени .

Интересно нарисовать картину распределения поля в разных случаях. Зададим, например, характер движения заряда. Пусть его поперечное ускорение зависит от времени, как показано на рисунке. Затем рассмотрим, как распределяется в пространстве напряженность электрического поля, создаваемого этим зарядом, через некоторый промежуток времени (рисунок). Поле в каждой точке определяется ускорением заряда в предыдущий момент времени (r / c секунд назад). Чем дальше точка, тем более ранним моментом времени определяется для нее ускорение. Поэтому кривая на рисунке в некотором смысле есть «обращенный» во времени график ускорения. Увеличив время на D t, можно восстановить значение а (r - r / c) добавлением отрезка D r = c D t, т.е. поле распространяется со временем как волна, уходящая от источника.

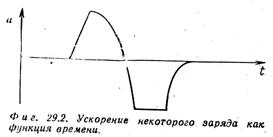
Особый интерес представляет случай периодических колебаний заряда q. Пусть смещение заряда определяется законом х = х ₀ соs w t. Ускорение в этом случае равно

а = -w² х ₀ соs w t = а ₀ соs w t

Зафиксируем вначале r и рассмотрим поле как функцию времени. Получается функция, которая осциллирует с угловой частотой w. Угловую частоту w можно определить как скорость изменения фазы со временем (радианы в секунду). Период есть время одного колебания, он равен 2p/w, так как произведение w и периода есть полный период косинуса.

Зафиксируем теперь время t и рассмотрим волну как функцию расстояния r. Если отвлечься от множителя 1/ r, то мы видим, что Е тоже осциллирует, когда меняется положение в пространстве. Тогда по аналогии с w введем так называемое волновое число и обозначим его через k. Оно определяется как скорость изменения фазы с расстоянием (радианы на метр). Время при таком изменении остается фиксированным.

Роль периода в пространстве здесь играет длина волны l. Длина волны есть расстояние, на котором колебание поля совершает один полный цикл. Длина волны равна l = 2p/ k, потому что k, умноженное на длину волны, равно полному периоду косинуса.

Запишем выражение для фазы волны j = w(t - r / c) и возьмем частную производную по r

Это соотношение можно записать разными способами:

l = с /n = 2p с /w

За время, равное одному периоду (1/n, где n - частота) волна пройдет расстояние с /n, с другой стороны, это расстояние должно быть равно длине волны l.

Энергия поля и его импульс

Локальные законы сохранения.

Энергия вещества сохраняется не всегда. При излучении, например, света объект теряет энергию. Поэтому закон сохранения не полон, если не рассмотреть энергию, связанную с электромагнитным полем.

Сделаем предположение о механизме выполнения закона сохранения энергии: если энергия уходит из какой-то области, то это может происходить только за счет ее вытекания через границы рассматриваемой области.

Пусть u обозначает плотность энергии поля, т.е. количество энергии в единице объема пространства, а вектор S - поток энергии поля (т.е. количество энергии, прошедшее в единицу времени через единичную поверхность, перпендикулярную потоку).

Пусть имеется объем V, ограниченный поверхностью S. Поток энергии поля из объема V равен интегралу от нормальной компоненты S по поверхности S:

Тогда закон сохранения энергии для данного объема можно выразить в следующей форме:

+ (Работа, затраченная на вещество в объеме V)

Найдем работу, затрачиваемую на вещество в единицу времени. Сила действующая на частицу F = q (E + v ´ B), а мощность равна F × v = q E × v. Если в единице объема содержится N частиц, то эта мощность в единице объема равна Nq E × v, а

Nq v = j (плотность тока). Таким образом, E × j должна быть равна энергии, теряемой полем в единице объема за единицу времени. Отсюда

Попытаемся переписать величину E × j в таком виде, чтобы она стала суммой двух слагаемых, зависящих от полей Е и В. Причем первое слагаемое должно быть производной по времени от некоторой величины, а второе - дивергенцией. Таким способом мы выразим через поля плотность и поток энергии электромагнитного поля.

Исходное выражение перепишем в виде:

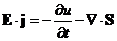
С помощью уравнений Максвелла попытаемся преобразовать задуманным образом величину E × j. Из уравнения для ротора В имеем

Итак, величина должна быть по крайней мере частью u. Такое же выражение получилось в электростатике. Осталось превратить в дивергенцию чего-то второе слагаемое. Путем громоздких преобразований с компонентами векторов можно доказать

Используя последнее равенство получаем:

Видим, что помимо производной по времени и дивергенции имеется среднее слагаемое., которое есть ни то и ни другое. В уравнениях Максвелла обнаруживаем, что ( равно . Это позволяет превратить среднее слагаемое в производную по времени:

Окончательно получаем:

Таким образом, можно определить u и S, как

Из выражения для плотности энергии видим, что она представляет сумму «электрической» и «магнитной» плотностей энергии, которые в точности равны выражениям, полученным в статике. Кроме того, получено выражение для вектора потока энергии электромагнитного поля. Этот новый вектор 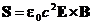по имени своего первооткрывателя называется «вектором Пойтинга». Он говорит нам о скорости, с которой энергия движется в пространстве. Энергия, протекающая в секунду через малую поверхность da, равна S × n da, где n - единичный вектор, перпендикулярный к поверхности da.

Не нашли, что искали? Воспользуйтесь поиском: