Постоянный электрический ток. Электричество и магнетизм

Электричество и магнетизм

Электростатика

Между заряженными и намагниченными телами действуют силы, называемые электромагнитными. Природа электромагнитных сил обусловлена электрически заряженными частицами, входящими в состав всех тел материального мира. Опытным путем установлено, что электрические заряды обладают следующими свойствами.

◦ Заряды бывают двух видов: положительные и отрицательные. Одноименные заряды отталкиваются, разноименные – притягиваются.

◦ Алгебраическая сумма зарядов изолированной системы постоянна.

◦ Электрический заряд является релятивистским инвариантом.

◦ Наименьшим по абсолютной величине элементарным зарядом, равным 1,6·10^-19 кулона (Кл) является отрицательный заряд электрона или равный ему по модулю положительный заряд протона.

Взаимодействие электрических зарядов описывает Закон Кулона: силы, с которыми два неподвижных точечных заряда Q и q действуют друг на друга в вакууме, пропорциональны произведению их величин и обратно пропорциональны квадрату расстояния между ними

, (1)

где = 8,85·10^-12 Ф/м – электрическая постоянная; - единичный вектор в направлении 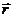(рис.1).

Заряды порождают в окружающем пространстве электрическое поле, проявляющееся в том, что помещенный в любую точку пробный заряд испытывает действие силы. Поле характеризуется векторной величиной, называемой напряженностью.

Напряженностью электрического поля называется отношение силы, действующей на электрический заряд q, к величине этого заряда

. (2)

Направление вектора совпадает с направлением силы, действующей на положительный пробный заряд. Подставляя вектор из формулы (2) в формулу (1) (в дальнейшем подобную операцию мы будем для краткости обозначать так: (2)®(1)), получим выражение для напряженности поля точечного заряда Q:

. (3)

Это выражение называют законом Кулона в полевой форме. Размерность напряженности в СИ: [E]=[ В/м ] - вольт на метр; =[ Н/Кл ] - ньютон на кулон,– здесь и далее в квадратных скобках мы будем обозначать размерности величин. По известной напряженности в любой точке поля легко найти силу, действующую на точечный заряд q, помещенный в эту точку поля:

. (4)

Принцип суперпозиции: сила, с которой система из n зарядов, действует на заряд q, не включенный в эту систему, равна векторной сумме сил, с которыми действует каждый заряд системы на заряд q:

. (5)

Отсюда следует и аналогичное выражение и для напряженностей:

. (6)

Напряженность поля системы точечных зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.

Электростатические поля изображают графически с помощью силовых линий – кривых в пространстве, касательные к которым в каждой точке совпадают с вектором . Густота силовых линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной силовым линиям, численно равнялось модулю вектора (рис.2).

Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. Поле, во всех точках которого вектор имеет одинаковую величину и направление, называется однородным (рис.2(1)). В остальных примерах поля неоднородны.

Поток вектора напряженности электрического поля. Рассмотрим сначала поле точечного заряда q с напряженностью . Опишем из этого заряда сферу радиуса r и площадью . Величина напряженности измеряется числом силовых линий, проходящих через единицу поверхности сферы, Þ полное число линий, пересекающих сферу равно

,

и не зависит от r! Таким образом, произведение ES (в данном примере это и есть поток) определяется величиной порождающего поле заряда и связано простым соотношением с напряженностью. Здесь уместно сравнить поток вектора напряженности с потоком вектора скорости жидкости, вытекающей из центра сферы равномерно во всех направлениях со скоростью u. В этом случае произведение uS представляет собой объем жидкости, вытекающий через поверхность сферы наружу в единицу времени. Введем теперь понятие потока вектора строго.

Потоком вектора напряженности электрического поля через поверхность S называется величина Ф_Е, равная

Ф_Е = = , (7)

где E_n – проекция вектора на направление нормали 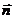(рис.3). Вектор имеет величину элементарной площади dS и направление, совпадающее с направлением нормали 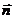к этой площадке.

Теорема Гаусса. Так называется выражение, связывающее поток Ф_Е вектора через произвольную замкнутую поверхность S с зарядом внутри нее. Найдем это выражение. Опишем из точечного заряда q сферу радиуса r. В каждой точке сферы вектор направлен перпендикулярно её поверхности и по величине равен . Поэтому поток Ф_Е через всю сферу равен

Ф_Е = , Þ

Ф_Е = . (8)

Окружим теперь заряд q поверхностью произвольной формы. Тогда поток dФ_Е через элемент dS этой поверхности (рис.4) равен

= . Интегрирование в пределах полного телесного угла W=4 p дает

, Þ

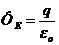. (9)

Поток Ф_Е равен заряду q внутри поверхности, деленному на e _о. Если заряд q находится вне замкнутой поверхности, то Ф_Е = 0. Действительно, пучок касательных, проведенных от заряда q (рис.5), делит замкнутую поверхность S на две части и . Потоки вектора через эти поверхности равны по величине, но имеют противоположные знаки, поэтому полный поток равен нулю.

Пусть теперь внутри замкнутой поверхности находится n точечных зарядов. По принципу суперпозиции результирующая напряженность равна векторной сумме напряженностей, создаваемых каждым зарядом системы в отдельности, следовательно

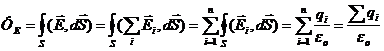,Þ

. (10)

Это теорема Гаусса: поток вектора напряженности электрического поля Ф_Е через любую замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на e _о.

Чтобы обобщить теорему Гаусса для непрерывного распределения заряда в пространстве с объемной плотностью r = 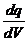, с поверхностной плотностью s = , или по линии с линейной плотностью l = , нужно суммирование в (10) заменить интегрированием: для заряда, распределенного по объему ;

по поверхности ;

по прямой .

Теорема Гаусса используется для упрощенного вычисления напряженности в случаях, обладающих достаточно высокой симметрией. Для краткости будем называть гауссовой ту (воображаемую, а не заряженную!) замкнутую поверхность S, по которой ведется интегрирование при вычислении потока.

Поле бесконечной равномерно заряженной плоскости. Пусть эта плоскость равномерно заряжена с поверхностной плотностью s >0. Вектор должен быть везде направлен перпендикулярно плоскости от нее. В противном случае существовала бы составляющая напряженности вдоль плоскости, что привело бы к перемещению зарядов и противоречило бы предположению о равномерном распределении заряда по плоскости. Также ясно, что во всех точках, равноудаленных от плоскости величина вектора должна быть одинакова. Поэтому в качестве гауссовой поверхности логично выбрать прямой цилиндр, расположенный симметрично относительно заряженной плоскости, как это показано на рис. 6. Поток вектора через боковую поверхность цилиндра равен нулю, так как там векторы и 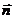взаимно перпендикулярны друг другу, Þ (, )=0, Þ на всей боковой поверхности =0. Поэтому полный поток равен сумме потоков через два основания 2 Е D S, где D S – площадь каждого основания цилиндра (и сечения цилиндра плоскостью тоже). Внутри цилиндра оказался заряд s D S (показан более плотной штриховкой). По теореме Гаусса 2 Е D S = s D S/e _о, Þ

. (11)

Следовательно, напряженность не зависит от расстояния до плоскости, и с каждой стороны от плоскости поле одинаково во всех точках, т.е. однородно.

Поле двух заряженных плоскостей. Пусть две параллельные плоскости равномерно заряжены с поверхностными плотностями + s и - s (рис.7). Поле справа и слева от плоскостей равно нулю (Е = s/ 2 e _о- s/ 2 e _о = 0), а между ними (Е = s/ 2 e _о+ s/ 2 e _о = s/e _о), следовательно

Е = s/e _о. (12)

Такое поле создается в плоском конденсаторе. Если плоскости заряжены одноименно, то поле между ними равно нулю, а снаружи описывается формулой (12). И, наконец, если модули не равны: |+ s | ≠ |- s |, то поле будет внутри больше, чем снаружи, но нигде не будет нулевым.

Поле бесконечного равномерно заряженного по поверхности цилиндра и нити. Пусть поверхность бесконечно длинного цилиндра радиуса R заряжена равномерно, и на единицу его длины приходится заряд l >0. Гауссову поверхность нужно взять в виде цилиндра высоты h и радиуса r (изображен пунктиром на рис.8), коаксиального с заряженным. Поток вектора через боковую поверхность гауссова цилиндра равен E 2 prh, а через основания – нулю, так как там вектор нормали перпендикулярен . Внутрь гауссовой поверхности попадает тонированная часть заряженного цилиндра, поэтому заряд внутри равен lh, поэтому при r>R по теореме Гаусса имеем E 2 prh = lh/e _о, Þ

, при r>R. (13)

Если R≠ 0, то при r ® R, . При r<R заряд внутри гауссова цилиндра отсутствует, Þ E 2 prh =0, Þ внутри цилиндра напряженность E =0. При R ®0, E ®¥. Таким образом вблизи тонкого острия можно создавать поля исключительно высокой напряженности, из-за чего заряды начинают стекать с острия в окружающее пространство. Формула (13) подходит и для нити, заряженной с линейной плотностью l. В этом случае условие r>R выполняется всегда.

Поле равномерно заряженной сферы. Пусть сфера радиуса R равномерно заряжена (не нужно говорить «по поверхности» - сфера это есть поверхность шара) с поверхностной плотностью

s >0. Вследствие центральной симметрии вектор в любой точке должен быть направлен вдоль радиуса от центра, а его модуль может зависеть только от расстояния r от центра. В качестве гауссовой поверхности выберем сферу радиуса r>R (рис.9). По теореме Гаусса поток вектора через эту сферу равен E 4 pr ²= , Þ вне сферы поле подобно полю точечного заряда:

, (14)

особенно если выразить s через полный заряд сферы q и её площадь 4 pR ²: s= q/ 4 pR ², откуда получим . На самой заряженной поверхности Е = s/e _о. При r<R заряда внутри гауссовой сферы нет, Þ внутри заряженной сферы напряженность Е =0.

Поле равномерно заряженного по объему шара. Пусть шар радиуса R равномерно заряжен с объемной плотностью ρ >0. Гауссову поверхность выберем так же, как для сферы (рис.9) При r>R, следуя теореме Гаусса, получаем E 4 pr ²= (чтобы найти заряд внутри, мы умножили ρ на объем шара радиуса R). Отсюда получим напряженность снаружи и на поверхности шара:

(r≥R). (15)

При r<R заряд внутрь гауссовой сферы попадает часть заряда шара, поэтому E 4 pr ²= , откуда напряженность внутри шара равна

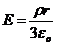(r<R). (16)

На рис. 10 представлены графики зависимости Е от r для равномерно заряженных плоскости (1), цилиндра (2), сферы (3) и шара (4).

Теорема о циркуляции вектора . В курсе механики было доказано, что работа поля центральных сил зависит только от начального и конечного положений частицы. Эквивалентным утверждением является: работа такого поля по перемещению частицы вдоль замкнутой траектории равна нулю. Такие поля называются потенциальными. Теорема о циркуляции вектора является выражением свойства потенциальности электростатического поля. Работа сил электростатического поля при перемещении точечного заряда q из точки 1 в точку 2 (рис.11):

.

Разделим эту работу на q:

. (17)

Отношение А/q это работа поля переноса единичного заряда из 1 в 2. Интеграл вида (17), вычисленный вдоль замкнутой траектории, называется циркуляцией вектора :

.

Теорема о циркуляции вектора утверждает: циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю: =0.

Доказательство. Электростатическое поле точечного заряда является полем центральных сил, и, следовательно, потенциальным. Поэтому работа его сил на замкнутом пути равна нулю: А = =0, Þ . Таким образом, циркуляция поля точечного заряда равна нулю. Докажем это и для системы n точечных зарядов. По принципу суперпозиции напряженность поля системы точечных зарядов равна: . Умножим это равенство скалярно на вектор перемещения 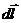вдоль произвольного замкнутого контура и проинтегрируем по этому контуру:

. (18)

Каждый интеграл в правой части равен нулю как циркуляция вектора напряженности электростатического поля отдельного точечного заряда, следовательно, и вся сумма равна нулю. Таким образом, циркуляция электростатического поля системы n точечных зарядов также равна нулю. Переходя к пределу в (18) нетрудно убедиться, что и для непрерывно распределенного заряда циркуляция электростатического поля равна нулю.

Потенциал. Из независимости от траектории интеграла следует, что его можно представить, как убыль некоторой функции координат:

, или (19)

. (20)

Введенная таким образом функция координат φ (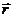) называется потенциалом. Разность потенциалов численно равна работе по переносу единичного положительного заряда из точки 1 в точку 2. Из того, что поле способно совершить такую работу, следует, что в точках 1 и 2 заряд обладает различной потенциальной энергией. Поэтому потенциал можно определить как потенциальную энергию пробного заряда q, отнесенную к его величине (правда саму потенциальную энергию всё равно придется вводить через ту же работу):

. (21)

Кроме того, из введенных определений (19,20), а также определения самой потенциальной энергии, следует, что потенциал определен с точностью до константы.

Потенциал поля точечного заряда. Поскольку заряд q создает поле с напряженностью (3), скалярное произведение в формуле (20) можно преобразовать:

= = =- , Þ

, где ,

и учтено, что 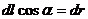(геометрия – на рис.12). Обычно полагают потенциал при r ®¥ равным нулю, тогда =0. В этом случае потенциал поля точечного заряда выражается формулой

. (22)

Если заряды распределены непрерывно с объемной плотностью ρ (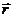), то точечным следует считать заряд . Тогда потенциал можно представить интегралом по объему

. (23)

Аналогично, если заряды распределены по поверхности или линии, то интегрируют по поверхности или линии соответственно

, . (24)

Единицей потенциала является вольт [ φ ] = [ В ].

Связь напряженности и потенциала. Пусть 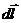- вектор малого перемещения вдоль траектории. Это значит, что радиус-вектор 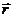(x, y, z) получил приращение . Тогда

= , (25)

откуда следует, что , , . Вектор в декартовых координатах можно представить суммой

= - .

Дифференциальную операцию в скобках, примененную к скалярной функции φ, называют градиентом этой функции (grad φ). Обратите внимание: grad φ – это векторная функция, полученная дифференцированием скалярной функции φ! Таким образом, связь напряженности и потенциала выражается формулой

. (26)

При решении задач бывает полезно найти проекцию на направление некоторого вектора . Так как = , то искомая проекция равна

. (27)

Эквипотенциальные поверхности. Так называются поверхности в пространстве, на которых потенциал имеет постоянное значение. Чтобы показать, что вектор всюду перпендикулярен эквипотенциальной поверхности, спроектируем его на касательный к этой поверхности вектор . Поскольку на эквипотенциальной поверхности, производная , Þ в соответствии с (27), равна нулю и проекция: =0. Если в некоторой точке проекция вектора на любое касательное направление к поверхности равна нулю, значит, этот вектор перпендикулярен поверхности. Таким образом, вектор перпендикулярен эквипотенциальной поверхности и направлен с учетом знака в сторону максимальной скорости убывания потенциала.

Потенциал системы зарядов. Напряженность поля системы точечных зарядов (6) равна

.

Умножим это выражение скалярно на вектор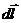

= .

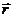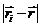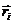Проинтегрируем это равенство с учетом того, что в знаменателе выражения (22) для потенциала точечного заряда стоит расстояние от заряда до точки с радиус-вектором , где вычисляется потенциал. Для каждого из n точечных зарядов системы это расстояние равно , где - радиус-вектор i -го заряда. Следовательно, потенциал поля системы точечных зарядов равен

. (28)

Итак, потенциал поля системы точечных зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов, независимо от других.

Чтобы получить потенциальную энергию заряда q в поле системы зарядов достаточно потенциал той точки, где находится заряд q умножить на потенциал этой точки

. (29)

Потенциальная энергия измеряется работой поля системы зарядов по переносу заряда q из точки с радиус-вектором 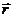на бесконечность.

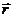Потенциал и напряженность электростатического поля диполя. Диполь – это система из двух разноименных зарядов, расположенных друг от друга на расстоянии , где - радиус-вектор произвольной точки А пространства относительно центра диполя (рис.13). Введем вектор дипольного момента: . Потенциал в точке А вычислим, как алгебраическую сумму потенциалов зарядов диполя

= .

Так как , положим ; . Тогда

.

Таким образом, потенциал поля диполя равен

. (30)

Напряженность поля диполя найдем в проекциях на вектор 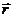(Е_r) и на перпендикулярное к 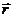направление (E_J):

; (31)

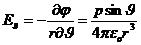
Модуль вектора найдем по теореме Пифагора

,

что после подстановки 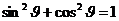дает

. (32)

Напряженность поля диполя убывает обратно пропорционально третьей степени расстояния – быстрее, чем поле точечного заряда. Из (32) легко получить и другие проекции вектора : параллельную (J =0) и перпендикулярную оси диполя (J = p/ 2):

; . (33)

Постоянный электрический ток

Электрический ток и вектор плотности тока. Ток в проводнике представляет собой направленное движение заряженных частиц. Сила тока (или просто ток) определяется как производная по времени от суммарного заряда Q (t), прошедшего через поперечное сечение проводника:

. (34)

Средней по сечению проводника плотностью тока называется отношение силы тока к площади сечения проводника . В общем случае плотность тока может быть разной в различных точках сечения. Величина вектора плотности тока численно равна заряду, протекающему в единицу времени через дифференциально малую площадку, перпендикулярную скорости направленного движения зарядов. За направление вектора плотности тока принимается направление средней скорости направленного движения зарядов. В соответствии с этими определениями, при концентрации n частиц в проводнике с зарядом е каждая, и их средней скорости направленного движения вектор плотности тока равен

. (35)

Выделим внутри проводника малую площадку dS (рис.14). Заряд, прошедший через нее за время dt, равен = , где α – угол между векторами и . Заряд , прошедший через все сечение проводника, равен интегралу , откуда ток, протекающий через все сечение проводника, равен

. (36)

Таким образом, сила тока является потоком вектора плотности тока. Единица силы тока называется ампер [ I ] = [ A ] и является основной электрической единицей в системе СИ, ее точное определение будет дано позднее.

Электродвижущая сила (эдс). Если проводник внести в электростатическое поле, то заряды будут двигаться до тех пор, пока их собственное поле не скомпенсирует поле внешнее, после чего практически мгновенно ток прекратится. Для поддержания тока к зарядам необходимо приложить силы не электростатической природы, называемые сторонними. Пусть на некотором участке цепи действуют сторонние силы с напряженностью и силы электростатического поля с напряженностью . Вычислим работу, необходимую для переноса заряда q из точки 1 в точку 2

= + .

Разделим обе части на q:

+ .

Величина U = называется напряжением и равна суммарной работе электростатических и сторонних сил по перемещению единичного положительного заряда из 1 в 2. Первое слагаемое = - это введенная ранее разность потенциалов (см.19), а второе называется электродвижущей силой (эдс), которая численно равна работе поля сторонних сил, необходимой для переноса единичного положительного заряда из точки 1 в точку 2

e = . (37)

Следовательно, U =() + e. (38)

Если точки 1 и 2 совпадают () – цепь замкнута, тогда эдс представляет собой циркуляцию вектора напряженности поля сторонних сил. Если на участке не действуют сторонние силы (такой участок называется однородным, эдс =0), то U = , Þ для однородного участка цепи напряжение совпадает с разностью потенциалов.

Закон Ома в дифференциальной форме описывает связь между векторами и . Пусть электрон движется в поле с напряженностью . По второму закону Ньютона, он приобретает ускорение , а его скорость возрастает по закону , где - скорость электрона в отсутствии внешнего поля. При каждом столкновении происходит передача кинетической энергии электрона кристаллической решетке, и скорость падает почти до нуля. Усредним выражение для скорости в пределах среднего времени между столкновениями t

.

Среднее значение скорости 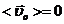вследствие хаотичности скорости в отсутствие поля. Поэтому . Учитывая определение (35), вектор плотности тока . Произведение констант, стоящих перед , также является некоторой константой s, Þ

. (39)

Этот результат называется законом Ома в дифференциальной форме: плотность тока в каждой точке проводника пропорциональна напряженности поля в этой точке. Величина s называется проводимостью. Этот закон с высокой точностью выполняется только для металлов.

Часто закон Ома в дифференциальной форме записывают в виде

, (40)

где ρ – удельное сопротивление, которое возрастает с увеличением температуры t, ^oC по закону:

, (41)

где α – температурный коэффициент сопротивления; ρ _о , a – табличные величины.

Закон Ома в интегральной форме. В простейшем случае для однородного участка цепи этот закон был установлен экспериментально

. (42)

Величина R (сопротивление проводника) зависит от его формы, температуры и материала

, (43)

где l – длина, S – площадь поперечного сечения проводника. Единицей сопротивления является ом: [ R ]=[ Ом ]. Размерность удельного сопротивления [ ρ ]=[ Ом × м ].

Рассмотрим неоднородный участок цепи, т.е. содержащий эдс. Реальный источник эдс можно рассматривать как идеальный, к которому последовательно присоединено его внутреннее сопротивление r (рис.15). Тогда U = I (R + r) ® (38), Þ

I (R + r)=() + e. (44)

Это закон Ома в интегральной форме: Произведение силы тока в проводнике на сумму внешнего и внутреннего сопротивлений равно сумме разности потенциалов на концах проводника и действующей в проводнике эдс.

В замкнутой цепи точки 1 и 2 совпадают и =0, поэтому закон Ома принимает вид

. (45)

Когда цепь разомкнута, ток равен нулю, и тогда

| | = e. (46)

Эдсисточника равна разности потенциалов на его зажимах при разомкнутой цепи.

Закон Джоуля-Ленца в интегральной форме. Работа А при перемещении заряда q из точки 1 в точку 2 равна

.

Мощность

, Þ

. (47)

Если на участке нет эдс, и вся работа тока идет на нагревание, то за время dt в проводнике выделится количество теплоты 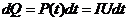. Поскольку , Þ . Интегрируя, получим з акон Джоуля-Ленца в интегральной форме:

. (48)

Если ток – постоянный, то выражение упрощается: .

Закон Джоуля-Ленца в дифференциальной форме. Вычислим энергию, которая выделяется в малом объеме проводника dV (рис.16), предполагая для простоты, что векторы плотности тока и напряженности поля сонаправлены, а вектор 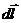выбран в том же направлении: ↑↑ ↑↑ 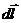. При перемещении заряда dq на 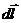поле совершает работу . Подставим и напряженность из закона Ома , тогда эта работа равна

.

Считая, что вся эта работа идет на нагревание (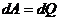), получим

,

где . Тогда теплота, выделяющаяся в единице объема проводника в единицу времени, равна

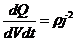. (49)

Величина слева называется удельной тепловой мощностью тока, а сам Закон Джоуля-Ленца в дифференциальной форме утверждает: удельная тепловая мощность тока пропорциональна квадрату плотности тока в той же точке.

Не нашли, что искали? Воспользуйтесь поиском: