Задача 1. Конденсатор переменной емкости

Тип задачи. Электростатическое поле.

Класс модели. Плоская (плоскопараллельная задача электростатики).

Единицы длины. Миллиметры.

Система координат. Декартовы координаты.

Геометрия:

Заряженные металлические пластины 1 и 2 разделены слоем воздуха и образуют обкладки плоского конденсатора. В зазор между обкладками на равном удалении от них помещена изолированная металлическая пластина толщиной . Геометрические размеры металлической пластины и обкладок конденсатора одинаковы. Перемещение пластины между обкладками конденсатора сопровождается изменением конфигурации зазора, активной площади заряженных пластин, а, следовательно, и емкости конденсатора. Пример геометрии поясняет один из важных принципов построения конденсатора переменной емкости.

Дано:

Ширина изолированной металлической пластины и обкладок конденсатора , их длина . Зазор между обкладками конденсатора в два раза больше толщины пластины Разность потенциалов между обкладками конденсатора

Относительная диэлектрическая проницаемость воздуха

Задача:

Построить картины электрического поля, определить заряд на поверхности заряженных металлических пластин и емкость плоского конденсатора в зависимости от глубины погружения изолированной металлической пластины в зазор между обкладками конденсатора.

Решение:

Для решения теоретически бесконечной задачи определим область расчета как прямоугольник площадью с тем, чтобы учесть влияние краевых эффектов. После построения геометрии в области моделирования по исходным данным присваиваем имена геометрическим объектам Пластина 1, Пластина 2, Воздух, Тело и задаем их свойства. Ребра и в модели отмечаем метками «Пластина 1» и «Пластина 2». В окне «Свойства метки ребра …» для пластины задаем значение потенциала , а для пластины соответственно . В окне «Свойства метки блока – Воздух» задаем значение относительной диэлектрической проницаемости воздуха . Изолированную металлическую пластину в модели представляем в виде прямоугольника, каждое ребро которого помечаем меткой Тело. В окне «Свойства метки ребра – Тело» устанавливаем флаг «Изолированный проводник (равный потенциал)». Решая задачу электростатики, находим распределение электрического поля в зависимости от глубины погружения 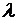изолированной металлической пластины внутрь плоского конденсатора.

Результат:

Картины электрического поля плоского конденсатора при различных значениях .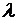

· Глубина погружения изолированной металлической пластины внутрь плоского конденсатора .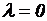

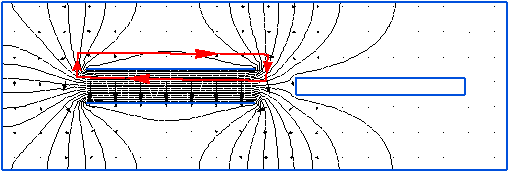
На картине электрического поля сплошными линиями обозначены линии равного электрического потенциала (число эквипотенциальных линий , ), а в виде стрелок - силовые линии поля. Длина стрелки на картине поля соответствует значению модуля вектора напряженности электрического поля. Максимум напряженности электрического поля . Для определения заряда на поверхности пластины плоского конденсатора зададим контур интегрирования, охватывающий ее целиком. Выполнив интегрирование по этому контуру, с помощью мастера «Мастер вычисления емкостей» получим заряд . Емкость конденсатора будет

.

· Глубина погружения изолированной металлической пластины внутрь плоского конденсатора . Число эквипотенциальных линий , , максимум напряженности электрического поля , заряд . Емкость конденсатора .

· Глубина погружения изолированной металлической пластины внутрь плоского конденсатора . Число эквипотенциальных линий , , , .

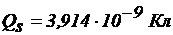Емкость конденсатора .

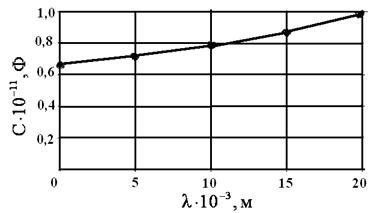
По результатам расчета картин электрического поля на рисунке приведена зависимость емкости плоского конденсатора от глубины погружения изолированной металлической пластины в зазор . Из графика видно, что зависимость с достаточной точностью можно аппроксимировать уравнением прямой линии.

Конденсаторы с воздушным диэлектриком применяют на практике наиболее часто, так как они характеризуются большей точностью установки ёмкости, малыми потерями и высокой стабильностью. Эти преимущества не относятся к конденсаторам с твёрдым диэлектриком, хотя они проще в изготовлении и имеют меньшие габариты.

Не нашли, что искали? Воспользуйтесь поиском: