Качественные методы исследования рекламы. При этом должно соблюдаться следующее равенство:

(26)

При этом должно соблюдаться следующее равенство:

(Х₁ —Х₂) + (Х₂—Х₃) = (Х₁ —Х₃), (27)

называемое свойством аддитивности, о котором мы поговорим позже.

К сожалению, мы не можем напрямую померить расстояния между марками, но мы можем опросить некоторое количество респондентов и попросить их сравнить попарно все три продукта и выбрать более предпочтительный. В нашем случае таких пар три:

Х₂-Х₂, Х₁-Х₃, Х₂-Х₃.

Опросив n респондентов, мы получаем матрицу предпочтений вида:

где п12 — количество респондентов, предпочитающих марку Х₁ марке Х₂, а n₂₁ — количество респондентов, предпочитающих марку Х₂ марке Х₁. Для

этих ячеек справедливо тождество:

(28)

Возникает естественный вопрос: каким образом можно преобразовать частоту предпочтений в расстояния? Один из подходов был предложен Максвеллом в 1974 г. в статье «Логистаческое преобразование в анализе парных сравнений», опубликованной в «Британском журнале математической и статистической психологии»¹. В качестве меры расстояния было предложено следующее выражение:

А. Кутлалиев

А. Попов

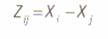(30)

и мы можем составить систему уравнений для вычисления координат

Х₁— Х_n.

Здесь нас поджидает одна неприятность — количество уравнений меньше количества переменных на единицу. Это связано с уже упомянутым — свойством аддитивности, которое связывает все расстояния тождеств: уменьшая число степеней свободы на 1. Но мы уже упоминали, что выбор начала координат сделан произвольно. Здесь приняты два подхода: либо мы принимаем, что координата одного из продуктов, например Х₁ равна 0, либо сумма координат равна 0.

Далее полученная система линейных уравнений решается любыми стандартными алгоритмами, и мы получаем шкалу, на которой отражены расстояния между исследуемыми марками продуктов.

Здесь необходимо вернуться к проблеме аддитивности. Понятно, что если Х₁> Х₂, а

Х₂ >Х₃, то Х₂ >Х₃. Но это в теории. На практике некоторые респонденты могут предпочесть первый продукт второму, второй — третье но потом вопреки всякой логике третий продукт первому. Логика и аддитивность прощаются с нами и желают приятного полета. Поэтому, после т как вы нашли расстояния, обязательно проверьте ваши данные на валидность. И не забудьте проверить статистическую значимость различий между

вычисленными координатами продуктов с помощью следующей статистики¹.

(31)

где V (Z_ij) дисперсия, вычисляемая по модифицированной формулу

Кокса2:

(32)

Далее по таблице нормального распределения определяется значимость различий.

До настоящего момента мы рассказывали о том, как метод парных, сравнений применяется для определения сходства и различия между разными марками продуктов. Покажем одно интересное применение метода

Глава 9.

Не нашли, что искали? Воспользуйтесь поиском: