ГЕОМЕТРИЧЕСКАЯ ОПТИКА

ОПТИКА

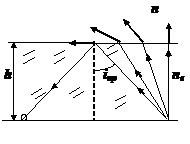
Елабуга

Печатается по решению Ученого совета Елабужского государственного педагогического университета.

ББК 22.31

С 12

УДК 530.1 (076)

Допущено Учебно-методическим объединением по направлениям педагогического образования Министерства образования Российской Федерации в качестве учебно-методического пособия для студентов, обучающихся по направлению 540200 Физико-математическое образование

Авторы-составители:

старший преподаватель кафедры общей физики Акулинина А.В.,

доценткафедры общей физики, канд. ф.-м. наук Сабирова Ф.М.

Рецензенты:

зав.кафедрой общей физики, канд. ф.-м. наук,

доцент ЕГПУ НАСЫБУЛЛИН Р.А.,

доцент кафедры физики Камского политехнического

института, канд. ф.-м. наук САРВАРОВ Ф.С.,

зав. каф. общенаучных дисциплин Елабужского филиала Казанского государственного технического университета, к.т.н., доцент КОНЮХОВ М.И.

Акулинина А.В., Сабирова Ф.М. Задачник-практикум по курсу общей физики. Оптика. / Учебно-методическое пособие для студентов физико-математического факультета педвуза и школьных учителей физики. - Елабуга: Изд-во Елабужского педун-та, 2004. - 50 с.

Елабужский государственный

педагогический университет, 2004. ã

ВВЕДЕНИЕ

Настоящее методическое пособие является продолжением серии пособий по курсу общей физики, изучаемой на физико-математических факультетах педвузов. Оно предназначено для проведения аудиторных практических и организации самостоятельных занятий по разделу “Оптика”. Материал методического пособия включает необходимые теоретические сведения, примеры решения задач и задачи для самостоятельной работы. Конкретная совокупность задач для решения в аудитории и домашних заданий определяется преподавателем, ведущим практические занятия. В конце многих разделов приведены и качественные задачи, которые могут обсуждаться как на практических, так и семинарских занятиях. В заключении указана использованная литература и некоторые справочные данные. Рисункам присвоена сквозная нумерация. Исключение составляют рисунки к задачам для самостоятельного решения, номера которых соответствуют номерам задач.

Пособие составлено с целью повышения эффективности организации самостоятельной работы и аудиторных занятий студентов очного и заочного отделений физико-математического факультета. Кроме того, пособие может быть рекомендовано для использования при проведении факультативных занятий школьников.

ФОТОМЕТРИЯ

Фотометрия – раздел оптики, в котором изучаются источники света, их характеристики, основные световые величины.

Мощность электромагнитного излучения, переносимого через единицу площади интервалом длин волн dl .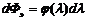

Функция распределения энергии по длинам волн .

Световой поток – энергия, переносимая волнами через единицу площади, за единицу времени, оцениваемой по зрительному ощущению. Y (l) – функция видности: Y (l)=0 для l < 0,4 мкм и l > 0,7 мкм; 1 ³ Y (l) > 0 для видимого света (l = 0,4 ¸ 0,7 мкм).

Полный световой поток: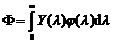

Световая энергия (за время t) при стационарном потоке: .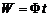

[Ф] = лм (люмен).

Источники света (солнце, звезды, пламя, лампы накаливания) делятся на точечные (размерами которых можно пренебречь) и протяженные.

Сила света ,

где dw – телесный угол (угол при вершине конуса, вырезающего на поверхности сферы радиуса R площадку dS). ;

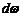[ ]=стер.(стерадиан) [ I ] = кд (кандела).

Если I = const – источник изотропный.

Полный световой поток от точечного изотропного источника .

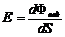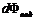Освещенность , где - световой поток, падающий на площадку 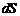. [ E ] = лк (люкс).

Освещенность, создаваемая точечным источником ,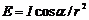

a - угол падения света в данную точку, r - расстояние от источника да точки.

Освещенность, создаваемая несколькими источниками Е=Е₁+Е₂+...+Е_n.

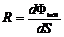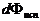Светимость , где - световой поток, испускаемый с поверхности по всем направлениям. [ R ] = лк (лм/м²).

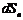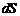
Яркость , где = – видимая светящаяся поверхность в данном направлении. [ B ] = нт (нит)

Если B =const - источник косинусный или ламбертовский. Светимость для косинусного излучателя. R=pВ.

Примеры решения задач.

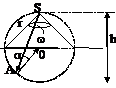Задача 1. Над полусферой на высоте h = 2 м, равный диаметру полусферы, находится точечный источник света S силой света I = 50 кд (см. рис.). Определите: а) световой поток, попадающий в полусферу; б) освещенность в той точке поверхности полусферы, в которую лучи падают под углом a=35^о.

Дано: h = 2 м= 2R, I= 50 кд, a = 35^о.

Найти: Ф -? Е -?

Решение. Световой поток Ф= Iw, где w - телесный угол, в котором распространяется световой поток, попадающий в полусферу.

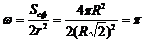(стер), так как r= 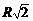. Отсюда Ф=Ip =157 (лм).

Освещенность в точке А: 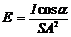, так как источник точечный. DSAO – равнобедренный. Поэтому SA/2=OA×cos a, SA=2R×cosa. ; E =15,3 лк. Ответы: Ф= 157 лм, E =15,3 лк.

Задача 2. Для освещения улицы применяются лампы силой света 300 кд, подвешенные на столбах на высоте 3 м. Расстояние между столбами 28 м. Определите освещенность поверхности земли посередине между столбами.

Дано: I₁ = I₂ = I =30 кд, h=3 м, l =28 м.

Найти: Е_с -?

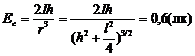Решение. Е_с = Е_1с + Е_2с = 2 Е_1с - освещенность в точке С, т. к. источников два и они расположены симметрично относительно точки С. Е_1с = Е_2с = , r²=h² + l²/4, cos a = h/r. Ответ: .

Задача 3. При фотографировании объекта, освещенного 100-ваттной лампой, расположенной на расстоянии 1 м от него, требуется экспозиция 8 с. Какова должна быть продолжительность экспозиции при освещении двумя 100-ваттными лампами, находящимися на расстояниях 3 м и 4 м, если общее количество энергии, попавшей на светочувствительную пластинку, должно быть таким же? Считать световую отдачу для всех ламп одинаковой.

Дано: Р₁=Р₂=Р₃= 100 Вт, t₁= 8 c, l₁= 1 м, l₂= 3 м, l₃= 4 м, W₁=W₂.

Найти: t₂ -?

Решение. По условию W₁=W₂, где W - количество световой энергии, попадающей на пленку: W= Ф t. Световой поток 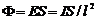, где Е - освещенность, I - сила света лампы, S - площадь пленки.

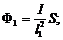
Сила света I для всех ламп одинакова, так как одинакова мощность и светоотдача. ; ; 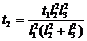t₂ = 46 c.

Задача 4. Вычислите и сравните между собой силы света раскаленного добела металлического шарика яркостью 3.10⁶ кд/м² и шарового светильника яркостью 3.10³ кд/м², если радиусы шарика и шарового светильника соответственно равны 1 мм и 10 см.

Дано:В₁= 3.10⁶ кд/м²; В₂= 3.10³ кд/м²; R₁ =10^-3 м; R₂ =0,1 м.

Найти: I₁ -? I₂ -? I₁ / I₂ -?

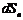Решение. – яркость источника, - видимая светящаяся поверхность. 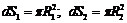-площади кругов.

Ответы: I₁ =9,42 кд, I₂ =94,2 кд, I₁ / I₂ =10.

Задача 5. Определите светимость волоска электрической лампы, если излучаемый световой поток равен 400 лм, длина волоска 60 см и диаметр его 0,04 мм.

Дано: Ф=400 лм, l = 60 м, d =4.10^-5 м.

Найти: R -?

Решение. R=Ф/S, где S - светящаяся поверхность, с которой испускается световой поток Ф. S=pdl. R=Ф/pdl, R =5,3.10⁶ лк.

Ответ: R =5,3.10⁶ лк.

Задача 6. Точечный источник света S освещает поверхность MN (см. рис.). Как изменится освещенность в точке А, в которую лучи от S падают нормально, если сбоку от S на таком же расстоянии, как и освещаемая поверхность, поместить зеркало Z, отражающее свет в точке А. Зеркало находится на одном уровне с источником S, коэффициент отражения принять равным 1.

Дано: SА= SВ.

Найти: Е₂/Е₁ -?

Решение. SА= SВ=r. E₁=I/r² - освещенность в точке А в отсутствие зеркала Z. Е₂=Е₁+Е’, где Е₁ - освещенность в точке А лучами, падающими нормально в эту точку.

Е’ = – освещенность в точке А, создаваемая лучами, отраженными зеркалом Z.

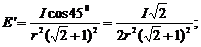
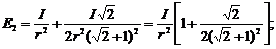
Ответ: Е₂/Е₁= 1,12.

Задачи для самостоятельного решения.

1.1. Свет от электрической лампочки в 200 кд падает под углом 45⁰ на рабочее место, его освещенность 141 лк. Найти: 1) на каком расстоянии от рабочего места находится лампочка, 2) на какой высоте от рабочего места она висит.

1.2. Лампа, подвешенная к потолку, дает в горизонтальном направлении силу света в 60 кд. Какой световой падает на картину площадью 0,5 м², висящую вертикально на стене в 2 м от лампы, если на противоположной стене находится большое зеркало на расстоянии 2 м от лампы?

1.3. В центре квадратной комнаты площадью 25 м² висит лампа. Считая лампу точечным источником света, найти, на какой высоте от пола должна находиться лампа, чтобы освещенность в углах комнаты была наибольшей.

1.4. В центре круглого стола диаметром 1,2 м имеется настольная лампа из одной электрической лампочки на высоте 40 см от поверхности стола. Над центром стола на высоте 2 м от его поверхности висит люстра из 4-х таких же лампочек. В каком случае получится большая освещенность на краю стола (и во сколько раз): когда горит настольная лампа или когда горит люстра?

1.5. Лампа, в которой светящим телом служит накаленный шарик диаметром 3 мм дает силу света в 85 кд. Найти яркость этой лампы, если сферическая колба лампы сделана: 1) из прозрачного стекла; 2) из матового стекла. Диаметр колбы равен 6 см.

1.6. Определить силу света светильников, подвешенных на расстоянии 10 м один от другого на одной стороне улицы, если освещенность на другой стороне улицы в наиболее удаленной от светильников точке составляет 5 лк. Ширина улицы равна 9 м. Светильники висят на высоте 6 м над землей.

1.7. Найти среднюю яркость кратера угольной дуги, если диаметр кратера 12 мм, а сила света в направлении, перпендикулярном к плоскости кратера, равна 18000 кд.

1.8. На высоте 3 м от земли висит лампа, сила света которой 250 кд, а на высоте 4 м висит лампа сила света которой 150 кд. Расстояние между лампами равно 2,5 м. Во сколько раз освещенность на земле под первой лампой больше, чем под второй.

1.9. На расстоянии d под поверхностью воды (с показателем преломления n) помещен точечный источник света S, сила света которого равна I. Небольшая площадка перемещается вдоль линии SA, оставаясь все время перпендикулярной этой линии (линия SA параллельна поверхности воды). Каково минимальное расстояние между площадкой и источником, при котором при подсчете освещенности площадки можно считать поверхность воды идеально отражающим зеркалом. Какова освещенность площадки на таком расстоянии?

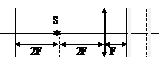1.10. На оптической скамье последовательно расположены экран, точечный источник света S, собирающая линза и плоское зеркало. Расстояния указаны на рис. Во сколько раз изменится освещенность в центре экрана, если плоское зеркало передвинуть вправо на расстояние F, равное фокусному расстоянию линзы?

1.11. 21 марта в день весеннего равноденствия, на Северной Земле Солнце стоит в полдень под углом α=10^о к горизонту. Во сколько раз освещенность площадки, поставленной вертикально, будет больше освещенности горизонтальной площадки?

1.12. Над центром круглого стола диаметром D = 2 м висит лампа с силой света I = 100 кд. Найти изменение освещенности Е края стола при постепенном подъеме лампы в интервале 0,5 м £ h £ 0,9 м через каждые 0,1 м. Построить график Е=f(h).

1.13. Предмет при фотографировании освещается электрической лампой, расположенной от него на расстоянии r₁=2 м. Во сколько раз надо увеличить время экспозиции, если эту же лампу отодвинуть на расстояние r₂ = 3 м от предмета.

1.14 На лист белой бумаги площадью S=20х30 см² перпендикулярно к поверхности падает световой поток Ф=120 лм. Найти освещенность Е, светимость R и яркость В бумажного листа, если коэффициент отражения ρ =0,75.

1.15 Экран Э и плоское зеркало Z образуют двугранный угол α=45^о (см.рис.). Между экраном и зеркалом на одинаковом расстоянии l от них помещен точечный источник света S. Какова освещенность экрана в точке А, если сила света источника I?

1.16 Точечный источник света, помещенный на расстоянии а от плоскости экрана, создает в центре его освещенность Е. Как изменится освещенность в центре экрана, если по другую сторону источника на расстоянии а /2 поместить вогнутое зеркало радиусом а.

1.17. Над горизонтальной поверхностью, освещенной точечным источником силой света 60 кд, на пути лучей поместили собирающую линзу так, чтобы источник находился в ее фокусе. Определить оптическую силу линзы, если освещенность поверхности под источником света 15 лк.

1.18. Над центром квадратной спортивной площадки на высоте 5 м висит лампа. Рассчитать, на каком расстоянии от центра площадки освещенность поверхности Земли в два раза меньше, чем в центре. Считать, что сила света лампы по всем направлениям одинакова.

1.19. Две лампы силой света I ₁=25 кд и I ₂=8 кд находятся друг от друга на расстоянии l =1,8 м. На каком расстоянии х от первой лампы (на линии, соединяющей лампы) надо поместить лист бумаги, чтобы освещенность его со стороны первой лампы была бы вдвое больше, чем со стороны второй лампы.

1.20. Между двумя экранами, установленными параллельно друг другу на линии, соединяющей их центры, расположен точечный источник света. Расстояние между источником и экранами относятся как 1:2. а) Каково отношение освещенностей в центрах экранов? б) Каким оно станет, если ближайший к источнику света экран повернуть так, чтобы угол падения на него света стал α=60^о.

1.21. На высоте h = 2 м над серединой круглого стола диаметром d =3м висит лампа силой света I₁=100 кд. Ее заменили лампой силой света I₂=25кд, изменив расстояние до стола так, что освещенность середины стола не изменилась. Как изменится освещенность края стола?

1.22. На столбе одна над другой висят две лампы силой света по I = 200 кд на высоте h=3м и h=4м над землей. Найти освещенность поверхности Земли на расстоянии l=2м от основания столба.

1.23. На высоте 3 м висят три лампы. Сила света каждой лампы равна 200 кд. Все они расположены на расстоянии 2,5 м друг от друга. Найти освещенность под каждой лампой.

1.24. Лампа, сила света которой 400кд, находится на расстоянии 1м от экрана. На каком расстоянии следует поставить позади лампы плоское зеркало, параллельное экрану, чтобы освещенность в центре экрана увеличилась на 100 лк?

1.25. Над столом на высоте 120 см и на расстоянии 80см от стены висит лампа, сила света которой 72 кд. Ниже лампы на стене вертикально висит зеркало (рис.), причем расстояние от его середины до лампы составляет 100 см. Определите освещенность на столе под лампой. Как изменится эта освещенность, если убрать зеркало.

ГЕОМЕТРИЧЕСКАЯ ОПТИКА

В основе геометрической оптики лежит представление о световых лучах - идеализированных бесконечно тонких пучках света, которые в однородной и изотропной среде распространяются прямолинейно. На основе этого понятия и законов отражения и преломления геометрическая оптика объясняет распространение световых пучков и их преобразование на границах раздела различных сред, не учитывая природу света.

Не нашли, что искали? Воспользуйтесь поиском: