ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ.

Линзы - прозрачные тела, ограниченные частями сферических поверхностей (частный случай - одна из поверхностей плоская). Световые лучи преломляются на обеих поверхностях линзы и дают изображение “действительное” (получается на пересечении преломленных лучей) или “мнимое” (получается на пересечении продолжения преломленных лучей). Собирающая линза - превращает световой пучок в сходящийся. Рассеивающая линза - превращает световой пучок в расходящийся.

Формула тонкой линзы (толщина линзы много меньше радиусов кривизны поверхностей) ,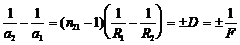

а₁ –расстояние от линзы до предмета, а₂ –расстояние от линзы до изображения, R₁, R₂– радиусы кривизны поверхностей, ограничивающих линзу, 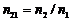– показатель преломления вещества линзы относительно окружающей среды, D–оптическая сила линзы, F–фокусное расстояние линзы.

Правило знаков: все отрезки отсчитывают от границы раздела; по ходу луча отрезки считают положительными, против хода луча – отрицательными. Для собирающей линзы D>0, для рассеивающей – D<0.

Поперечное увеличение линзы: , где h₁, h₂ - поперечны размера предмета и изображения.

Увеличение оптической системы: 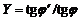, где j¢, j – углы, под которыми рассматривают предмет с помощью прибора и без него.

Примеры решения задач.

Задача 1. Цилиндрический пучок лучей, параллельных главной оптической оси рассеивающей линзы, имеет диаметр d₁ = 5 см. Пройдя линзу, пучок дает на экране пятно диаметром d₂ = 7 см. Каким будет диаметр d₃ пятна, если рассеивающую линзу заменить собирающей с тем же фокусным расстоянием?

Дано: d₁=5 см, d₂=7 см, F₁=F₂=F

Найти: d₃ -?

Решение. Лучи, параллельные главной оптической оси, после преломления на рассеивающей линзе идут так, что их продолжение идет через фокус F₁; для собирающей линзы преломленные лучи идут через фокус F₂. Обозначим расстояние от линзы до экрана – b. Тогда из подобия треугольников DABF_1,2 и DCDF_1,2

Приравнивая правые части равенств (3) и (4), получаем: 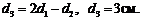Ответ: d₃=3 см.

Задача 2. В куске стекла с показателем преломления n_cт=1,5 имеется воздушная полость в виде двояковыпуклой линзы с радиусами кривизны поверхностей R=10 см. На оптической оси этой линзы внутри куска стекла на расстоянии 20 см от линзы находится песчинка. Определить расстояние между изображением песчинки и линзой.

Дано:n_возд= 1, n_cт =1,5, R₁=R₂=R=10 см, a₁ =20 см

Найти: а₂ –?

Решение. По формуле тонкой линзы

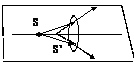
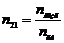– относительный показатель преломления вещества линзы относительно окружающей среды.

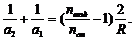
Отсюда 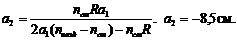Знак (–) означает, что изображение “мнимое”, то есть линза в данном случае рассеивающая. Ответ: а₂ = –85 см.

Задача 3. Оптическая система состоит из собирающей линзы с фокусным расстоянием F и плоского зеркала, расположенного перпендикулярно к главной оптической оси. Расстояние между линзой и зеркалом 4F. Точечный источник света находится на главной оптической оси посредине между линзой и зеркалом. найти расстояние между действительными изображениями источника.

Дано: a₁=a₁’=2F, L=4F

Найти: S₁S₂ –?

Решение. Пучок света от источника S попадает частично на плоское зеркало. Лучи, преломленные на линзе, дают изображение S₁. Лучи. отраженные от зеркала, падают на линзу и, преломляясь, дают изображение S₂. При этом изображение точки S в зеркале S’ является для линзы источником.

По формуле тонкой линзы . Отсюда По формуле плоского зеркала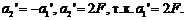

Изображение точки S в плоском зеркале S’ – мнимое.

.

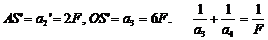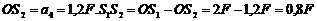
Отсюда 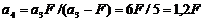Ответ: OS₂=0,8 F.

Задача 4. Зрительная труба с фокусным расстоянием 50 см установлена на бесконечность. После того как окуляр трубы передвинули на некоторое расстояние, стали видны предметы, удаленные от объектива на 50 м. На какое расстояние передвинули окуляр при наводке.

Дано: a₁=¥, a₁’=50 м, F₁= 50 см = 0,5 м.

Найти: D l –?

Решение. Так как вначале объектив зрительной трубы установлен на бесконечность, то есть a₁=¥, то изображение, даваемое объективом, попадает в фокальную плоскость объектива а₂ =F₁. Согласно формуле тонкой линзы Это изображение попадает и в фокальную плоскость окуляра, т.к. задний фокус объектива совпадает с передним фокусом окуляра, играющего роль лупы. Если а₁ ’=50 м, то .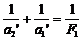

Отсюда 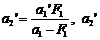=0,505 м=50,5 см. В этом случае изображение, даваемое объективом, сместилось вправо на расстояние

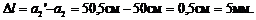
На такое же расстояние следует передвинуть и окуляр зрительной трубы, чтобы изображение попало в фокальную плоскость окуляра. (Указание: ход лучей в зрительной трубе смотрите в теории к данному разделу.)

Задачи для самостоятельного решения.

4.1. Из двух стекол с показателями преломления 1,5 и 1,7 сделаны две одинаковые двояковыпуклые линзы. 1)Найти отношение их фокусных расстояний. 2) Какое действие каждая из этих линз произведет на луч, параллельный оптической оси, если погрузить линзы в прозрачную жидкость с показателем преломления 1,6?

4.2. Линза с фокусным расстояние 16 см дает резкое изображение предмета при двух положениях, расстояние между которыми 60 см. Найти расстояние от предмета до экрана.

4.3. Найти фокусное расстояние линзы, погруженной в воду, если известно, что ее фокусное расстояние в воздухе равно 20 см. Показатель преломления стекла, из которого сделана линза, равен 1,6.

4.4. В фокальной плоскости двояковыпуклой линзы расположено плоское зеркало. Предмет находится перед линзой между фокусом и двойным фокусным расстоянием. Построить изображение предмета.

4.5. На экран с круглым отверстием радиуса 10 см падает сходящийся пучок света. Угол между крайним лучом и осью симметрии равен 30^о. Определите точку. в которой будут сходиться лучи, если в отверстие вставляется: 1) собирающая; 2) рассеивающая линзы. D₁=D₂ =10 диоптрий.

4.6. Сходящийся пучок, проходящий через отверстие диаметром 6 см в непрозрачном экране I, падает на экран II, находящийся за экраном I на расстоянии 50 см, светлое пятно диаметром 3 см. После того как в отверстие I поместили линзу, пятно превратилось в точку. Найти фокусное расстояние линзы.

4.7. Собирающая линза с фокусным расстоянием F=20 см состоит из двух половинок. Определить расстояние между изображениями точечного источника, если половинки раздвинуть: 1) на расстояние d₀=1 см перпендикулярно главной оптической оси; 2) на то же расстояние одна из половинок сдвигается от источника вдоль оптической оси; 3) не раздвигая линзу, закрыть ее среднюю часть непрозрачным экраном диаметром d₀. Источник расположен на расстоянии 75 см от линзы.

4.8. Собирающая и рассеивающая линзы имеют общую оптическую ось. Фокусные расстояния равны соответственно F₁= a, F₂=–b (a > b). Лучи, параллельные оси, после прохождения системы не изменяют направления. Найти расстояние между линзами.

4.9. Найдите построением ход луча 2 после тонкой линзы, если известен ход луча 1.

4.10. Постройте изображение точки А, находящейся на оптической оси рассеивающей линзы.

4.11. На рисунке показаны положения оптической оси тонкой линзы MN, точки S и ее изображения S’. Найдите построением положение центра тонкой линзы и ее фокусов.

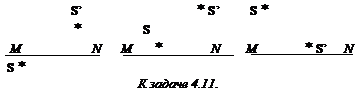
4.12. Световой пучок от источника S, находящегося в фокальной плоскости тонкой линзы, падает на линзы. Показать ход этих лучей после линзы.

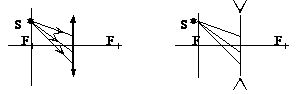
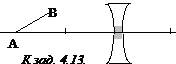4.13. Средняя часть линзы заклеена черной бумагой. Найдите построением изображение предмета АВ.

4.14. Параллельный пучок света падает на линзу, затем на вогнутое зеркало. Фокусное расстояние зеркала равно 24 см. Расстояние между линзой и зеркалом 32 см. Каким должно быть фокусное расстояние линзы, чтобы свет, отразившись от зеркала, собрался в точке, удаленной от зеркала на расстояние 6 см.

4.15. Увеличение микроскопа 600. Определите оптическую силу объектива, если фокусное расстояние окуляра F_ок=4 см, а длина тубуса l= 24см.

4.16. В отверстие в экране вставлена рассеивающая линза с фокусным расстоянием 10см, на которую падает параллельный пучок лучей. На расстоянии 30 см от линзы параллельно ее плоскости расположен экран. При замене рассеивающей линзы на собирающую такого же диаметра радиус светлого пятна на экране не изменился. Чему равно фокусное расстояние собирающей линзы?

4.17. Действительное изображение предмета, полученное с помощью собирающей линзы, находится от нее на расстоянии 8см. Если собирающую линзу заменить рассеивающей с таким же фокусным расстоянием, мнимое изображение этого предмета будет отстоять от линзы на 2см. Найти абсолютную величину фокусного расстояния линз (в мм).

4.18. Два точечных источника света находятся на расстоянии 24см друг от друга. Между ними на расстоянии 6 см от одного из них помещена собирающая линза. При этом изображения обоих источников получились в одной и той же точке. Найдите фокусное расстояние линзы (в см.).

4.19. Вдоль оптической оси собирающей линзы с фокусным расстоянием 5 см расположен стержень так, что его середина находится на расстоянии 8 см от линзы. Чему равна (в см) длина этого стержня, если его продольное увеличение равно 5.

4.20. Тонкий стержень расположен вдоль главной оптической оси собирающей линзы. Каково продольное увеличение стержня, если объект, расположенный у одного конца стержня изображается с увеличением 2,75? Оба конца стержня расположены от линзы на расстоянии больше фокусного.

4.21. На оси тонкой рассеивающей линзы с фокусным расстоянием 5см и диаметром d=2 см на расстоянии 20 см от нее находится точечный источник света. По другую сторону линзы на расстоянии 10 см от нее расположен экран. Найти диаметр D светлого пятна на экране.

4.22. Небольшое тело находится на горизонтальной подставке на оси собирающей линзы с фокусным расстоянием F. Расстояние между линзой и телом равно 2F. Телу сообщают скорость u, направленную от линзы вдоль ее главной оптической оси. Коэффициент трения о подставку равен µ. Какое расстояние пройдет изображение тела в линзе к моменту остановки тела?

4.23. Небольшой шарик, подвешенный на нити длиной l вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через точку подвеса. Под шариком на расстоянии а от плоскости вращения закреплена тонкая собирающая линза с фокусным расстоянием F (F< а) так, что ее главная оптическая ось совпадает с осью вращения шарика. Найти угловую скорость шарика, если его изображение вращается по окружности радиусом R.

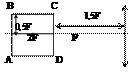4.24. Квадрат со стороной равной фокусному расстоянию тонкой собирающей линзы расположен так, как показано на рисунке. Построить изображение квадрата и найти отношение площадей квадрата и его изображения.

4.25. Точечный источник света находится под поверхностью жидкости на глубине h = 20 см. С помощью тонкой собирающей линзы получают уменьшенное изображение поверхности жидкости на экране, отстоящем от поверхности на расстоянии l =10 см. Фокусное расстояние линзы F=1,6 см. Определить радиус освещенного пятна на экране. Показатель преломления жидкости n=1,5.

4.26. Собирающая линза с оптической силой Д₁=2дптр и рассеивающая линза с оптической силой Д₂=-1,5дптр расположены на расстоянии а =40 см друг от друга и имеют общую оптическую ось. Со стороны собирающей линзы на расстоянии 4м от нее находится предмет высотой h=20см. Определить, где и какое изображение предмета дадут эти линзы. Предмет расположен на оптической оси линзы, параллельно ее плоскости.

4.27. На оси ОХ в точке х₁=0 находится оптический центр тонкой рассеивающей линзы, а в точке х₂=15см – тонкой собирающей линзы с фокусным расстоянием F₂=15см. Главные оптические оси обеих линз лежат на оси ОХ. На рассеивающую линзу падает параллельный пучок света вдоль оси ОХ из области х<0. Пройдя данную оптическую систему, лучи собираются в точке с координатой х₃=45см. Найдите фокусное расстояние рассеивающей линзы F₁.

4.28. На оси ОХ в точке х₁=15см находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием F₁=–15 см, а в точке х₂=27,5см – тонкой собирающей линзы. Главные оптические оси обеих линз совпадают с осью ОХ. Свет от точечного источника, расположенного в точке х=0, пройдя данную оптическую систему, распространяется параллельным пучком. Найдите фокусное расстояние собирающей линзы F₂.

4.29. На оси ОХ в точке х₁=0 находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием F₁=–30см, а в точке х₂=30 см – тонкой собирающей линзы с фокусным расстоянием F₂=30см. Главные оптические оси обеих линз лежат на оси ОХ. На рассеивающую линзу по оси ОХ падает параллельный пучок света из области х<0. Найдите координату х точки (в см), в которой собирается этот пучок, пройдя данную оптическую систему.

4.30. Линза, фокусное расстояние которой 20см дает на экране изображение предмета с 4-х кратным увеличением. Экран подвинули к линзе вдоль ее главной оптической оси на 40см. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. Определите увеличение во втором случае.

4.31. Линза, фокусное расстояние которой 12 см, дает на экране изображение предмета с четырехкратным увеличением. Экран передвинули вдоль главной оптической оси линзы. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. В этом случае получено изображение с трехкратным увеличением. На сколько пришлось сдвинуть предмет относительно его первоначального положения?

4.32. Из плоскопараллельной стеклянной пластинки изготовили 3 линзы, разрезав ее так, как показано на рисунке. Фокусное расстояние линз1 и 2, сложенных вместе равно – F, фокусное расстояние линз 2 и 3 равно – F. Определите фокусное расстояние каждой из линз отдельно.

ИНТЕРФЕРЕНИЯ СВЕТА

Интерференция света - особый случай сложения волн, при котором в одних точках волны усиливают друг друга, а в других точках волны гасят друг друга. Интерферируют только когерентные волны.

Условие когерентности: w₁= w₂; Dj = const, частоты колебаний равны, а разность фаз слагаемых волн постоянна.

Интерференционная картина – чередование максимумов (max) и минимумов (min) освещенности (светлых и темных полос). Положение светлых и темных полос определяется условиями:

максимума и минимума ,

где – разность оптического хода волн, l – длина волны, k =0, 1, 2, 3,... – порядок максимума (минимума).

При двулучевой интерференции (опыты Юнга, Френеля) координата k-ой светлой полосы: ,

где L - расстояние от источников когерентных волн до экрана, d – расстояние между источниками когерентных волн. Расстояние между соседними интерференционными полосами (ширина полосы) .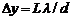

Примеры решения задач.

Задача 1. Определите расстояние между когерентными источниками в опыте Юнга, если на экране на протяжении 10,8 мм лежит шесть интерференционных полос. Расстояние от источников до экрана 3 м. Длина волны монохроматического света 6000 .

Дано: b = 10,8.10^-3м, N = 6, L=3м, l=6.10^-7м.

Найти: d –?

Решение.

В опыте Юнга источниками когерентных волн являются щели в экране II (по принципу Гюйгенса).

Пусть S₁S₂=d; OB=L. В точке А наблюдается k-ый максимум. ОА=у_k – координата максимума, – разность хода волн от источников S₁ и S₂, встречающихся в точке А. Из рисунка

,

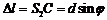где 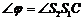. 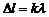- по условию максимума. Следовательно .

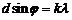Из DОАВ: 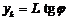. Угол j мал, так как d<<L. Тогда – координата (k+1)-го максимума. 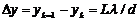– расстояние между соседними интерференционными полосами. По условию задачи 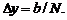Поэтому 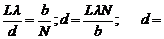10^-3 м = 1 мм. Ответ: d=1 мм.

Задача 2. В точках А и В находятся когерентные источники световых волн (l=550 нм). На сколько изменится разность хода и разность фаз колебаний, приходящих в точку О, если на пути АО поместить мыльную пленку толщиной 1 мкм? Показатель преломления 1,33.

Дано: l=5,5.10^-7м, d=10^-6м, n=1,33

Найти: D l-? D l ’-? D j -?

Решение.

D l= l₂ – l₁ - разность оптического хода волн, встречающихся в точке О, где l₂ =ВО, l₁ =АО, l₁,l₂ - оптические длины путей лучей в воздухе.

D l’= l₂’ – l₁’ - разность оптического хода лучей с мыльной пленкой.

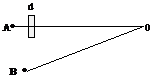
l₁’ = l₁ – d+dn=l₁+ d(n –1) - оптическая длина пути луча АО, Þ D l’= l₂ – l₁ – d(n-1).

Поэтому разность оптического хода меняется на величину:

D l – D l’= l₂ – l₁ – l₂ + l₁ +d (n-1) = d (n-1).

D l – D l’ = d (n-1) = 10^-6(1,33-1)=3,3.10^-7м.

Разность фаз связана с разностью хода волн соотношением: 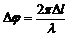. Поэтому изменение разности фаз: .

Задача 3. Угол между зеркалами Френеля a=10’. На зеркала падает свет от щели, находящейся на расстоянии 10 см от линии пересечения зеркал. Длина световой волны источника l=600 нм. Отраженный от зеркал свет дает интерференционную картину на экране, расположенном на расстоянии L=270 см от линии пересечения зеркал. определите расстояние между интерференционными полосами на экране.

Дано: a=10’, r =0,1 м, l=600 нм=6.10^-7м, L=2,7 м

Найти: D х –?

Решение. В опыте с зеркалами Френеля (угол между ними близок к 180^о) мнимые изображения источника S₁,S₂ в зеркалах играют роль когерентных источников. При отражении света от двух зеркал на экран падают два световых пучка (см. рис.) Так как эти пучки идут от одного и того же источника, то они когерентны и, перекрываясь, дают на экране интерференционную картину.

Расстояние между интерференционными полосами на экране (ширина интерференционной полосы) может быть рассчитана по формуле: 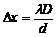, где D =ОВ+ОА=ОВ+ L, ÐS₂OS₁=2a. Тогда 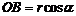. Следовательно, . Отсюда 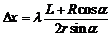. a=10’, поэтому сos a» 1, sin a»0,0029. 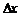= 2,9.10^-3м =2,9 мм.

Анализируя данный результат, легко заметить, что d должно быть малым, чтобы интерференционные полосы можно было различать. Следовательно, и угол a должен быть мал (порядка нескольких минут). Если a=3^о, то 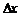= 10^-7 м, то есть полосы такой ширины недоступны наблюдению.

Задачи для самостоятельного решения.

5.1. Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (l=5.10^-5см) заменить красным (l=6,5.10^-5см)?

5.2. В опыте Юнга отверстия освещались монохроматическим светом длиной волны l=6.10^-5см, расстояние между отверстиями 1 мм и расстояние от отверстий до экрана 3 м. Найти положение трех первых светлых полос.

5.3. В опыте Юнга на пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка, вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает на пластинку перпендикулярно. Показатель преломления пластинки 1,5. Длина волны l=6.10^-7 м. Какова толщина пластинки?

5.4. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света было равно 0,55 мм, расстояние до экрана 5 м. В зеленом свете получились интерференционные полосы на расстоянии 5 мм друг от друга. Найти длину волны зеленого света?

5.5. От узкой щели при помощи бипризмы Френеля с преломляющим углом j=20’ получают на экране интерференционную картину. Щель расположена на расстоянии r=25 см от бипризмы, а экран на расстоянии L=100 см. Определите длину волны света, освещающего щель, если ширина интерференционных полос на экране Dх=0,55 мм.

5.6. На пути одного луча в опыте Юнга поставлена трубка с плоскопараллельными стеклянными основаниями длиной l= 2 см. При заполнении трубки хлором вся интерференционная картина на экране смещалась на N=20 полос. Вычислите показатель преломления хлора, считая, что показатель преломления воздуха n_в=1,000276, длина волны света, даваемого источником, l=589 нм.

5.7. Свет прошел в сероуглероде 20 см. Какой путь пройдет свет за то же время в воде? Чему равняется оптическая длина пути света в воде и в сероуглероде? Показатель преломления сероуглерода 1,63, показатель преломления воды 1,33.

5.8. Два точечных когерентных источника света находятся в спирте (n =1,36) на расстоянии 1 см друг от друга. Определить оптическую разность хода для точки, лежащей на расстоянии 20 см от одного из источников по направлению нормали к прямой, соединяющей источники.

5.9. Два когерентных источника, находящихся в воздухе на расстоянии 20 мм, испускают световые волны в одинаковой фазе с частотой 5.10¹¹ Гц. Чему равняется разность фаз колебаний, приходящих в точку, удаленную на 50 см от одного из источников в направлении нормали к прямой, соединяющей источники?

5.10. Определите длину отрезка l ₁, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке l ₂ = 5 мм в стекле. Показатель преломления стекла n=1,5.

5.11. Два параллельных световых пучка, отстоящих друг от друга на расстоянии d = 5 см, падает на кварцевую призму (n=1,49) с преломляющим углом α = 25⁰. Определите оптическую разность хода Δ этих пучков на выходе из призмы.

5.12. В опыте Юнга расстояние l от щелей до экрана равно 3 м. Определите угловое расстояние между соседними светлыми полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на 4,5 мм.

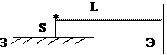5.13. Точечный источник монохроматического света находится на расстоянии S=1 мм от большого плоского зеркала З на расстоянии L=4 м от экрана Э, перпендикулярного зеркалу (см. рис.). Каково расстояние х между соседними максимумами освещенности на экране, если длина волны λ=600 нм.

5.14. Два плоских зеркала образуют двугранный угол α=179,5⁰ (см. рис.) На одинаковых расстояниях d=10 см от каждого из зеркал расположен точечный источник А монохроматического света с длиной волны λ=600 нм. Найдите расстояние х между серединами соседних светлых интерференционных полос на экране, расположенном на расстоянии L=3 м от линии пересечении зеркал. Свет непосредственно от источника на экран не попадает.

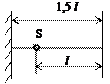5.15. Точечный источник монохроматического света с длиной волны λ=500 нм расположен на расстоянии l =50 см от экрана, а на расстоянии 1,5 l от экрана находится параллельное экрану плоское зеркало (см. рис.). Какой вид имеет интерференционная картина на экране? Темная или светлая интерференционная полоса проходит на расстоянии 2 мм от точки 0 на экране.

Не нашли, что искали? Воспользуйтесь поиском: