
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ДИФРАКЦИЯ В ПАРАЛЛЕЛЬНЫХ ЛУЧАХ (ФРАУНГОФЕРА)
Дифракция на щели. При освещении щели пучком параллельных лучей, падающих нормально, каждая точка щели становится источником вторичных когерентных волн. Волны, идущие под углом j к первоначальному направлению, собираются в точке Р в фокальной плоскости линзы L и интерферируют. Дифракционная картина от щели – чередование светлых и темных полос (максимумов и минимумов освещенности).
Условие максимума  .
.
Условие минимума  .
.
Здесь b – ширина щели, j – угол дифракции, k = 1, 2,... – порядок максимума (минимума), l – длина волны.
Интенсивность в точке экрана, положение которой определяется углом дифракции j:  ,
,
где I0 – интенсивность света в центре дифракционной картины.
Дифракционная решетка – система узких параллельных щелей, разделенных непрозрачными промежутками. b+c=d – период (постоянная) решетки; b - ширина щели, c - ширина непрозрачного промежутка.
Дифракционная картина от решетки – узкие яркие полосы на темном фоне (главные максимумы).
Условие главного максимума  ,
,
где m – порядок главного максимума.
Характеристики решетки как спектрального прибора:
угловая дисперсия  ;
;
dj – угловое расстояние между двумя линиями в спектре данного порядка с разностью длин волн dl.
линейная дисперсия 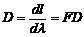 ;
;
dl – линейное расстояние между двумя линиями в спектре данного порядка; F – фокусное расстояние линзы;
разрешающая способность 
dl – минимальная разность длин волн двух линий в спектре данного порядка при условии. что эти линии видны раздельно; N – число щелей в решетке;
Угловое расстояние  между двумя точками, разрешаемыми телескопом:
между двумя точками, разрешаемыми телескопом:  , где D – диаметр объектива.
, где D – диаметр объектива.
Расстояние d, разрешаемое объективом микроскопа:  где l – длина световой волны, n – показатель преломления среды (между предметом и объективом), a – половина угла между лучами, идущими от объекта к краям объектива.
где l – длина световой волны, n – показатель преломления среды (между предметом и объективом), a – половина угла между лучами, идущими от объекта к краям объектива.
Примеры решения задач.
 Задача 1. На щель шириной 2.10-3 см падает нормально параллельный пучок монохроматического света с длиной волны 5.10-5 см. Найти ширину изображения щели на экране, удаленном от щели на расстояние 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, расположенными по обе стороны от главного максимума освещенности.
Задача 1. На щель шириной 2.10-3 см падает нормально параллельный пучок монохроматического света с длиной волны 5.10-5 см. Найти ширину изображения щели на экране, удаленном от щели на расстояние 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, расположенными по обе стороны от главного максимума освещенности.
Дано:b =2.10-5м, l =5.10-7 м, l =1 м.
Найти: d –?
Решение. Дифракционная картина от щели – чередование максимумов и минимумов освещенности (светлых и темных полос). В центре картины - светлая полоса или расширенное изображение щели. d =|AB| - ширина изображения щели. Точки А и В определяют положения минимума первого порядка, которые определяются из условия:  , где k =1. Отсюда:
, где k =1. Отсюда:  . Из DОАВ:
. Из DОАВ:  , но для малых углов
, но для малых углов  , следовательно:
, следовательно: 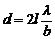 ; d =5.10-2 (м)=5 см. Ответ: d = 5 см.
; d =5.10-2 (м)=5 см. Ответ: d = 5 см.
Задача 2. На дифракционную решетку, имеющую 500 штрихов на 1 мм, нормально падает белый свет. Непосредственно за решеткой помещена линза с фокусным расстоянием 2 м, проецирующая спектры на экран. Диапазон длин волн видимого спектра lф=400 нм, lкр=700 нм. а) Могут ли перекрываться спектры первого и второго порядка? б) Во сколько раз спектр второго порядка на экране длиннее спектра первого порядка? в) Какова разность углов отклонения конца первого и начала второго порядка?
 Дано: n=500
Дано: n=500  =5,105
=5,105  , F=2 м, lф=4.10-7м, lкр=7.10-7 м
, F=2 м, lф=4.10-7м, lкр=7.10-7 м
Найти: а)  б)
б)  в)
в) 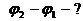
Решение. При освещении решетки белым светом на экране наблюдаем дифракционный спектр – все максимумы, кроме нулевого, цветные полосы, обращенные фиолетовым концом к нулевому максимуму. Положения максимума определяются из условия  , где d - период решетки:
, где d - период решетки:  (расстояние между соседними штрихами). Чтобы узнать, перекрываются ли спектры первого и второго порядков, определим углы дифракции для красного конца спектра первого порядка и фиолетового конца спектра второго порядка
(расстояние между соседними штрихами). Чтобы узнать, перекрываются ли спектры первого и второго порядков, определим углы дифракции для красного конца спектра первого порядка и фиолетового конца спектра второго порядка  и
и  :
:



Так как  – это означает, что спектры не перекрываются. По значениям углов
– это означает, что спектры не перекрываются. По значениям углов  определим разность углов отклонения:
определим разность углов отклонения: 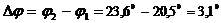 .
.
Длина спектра k-го порядка  , где
, где  – углы дифракции, определяющие положение краев спектров, а углы дифракции находим из условия главных максимумов
– углы дифракции, определяющие положение краев спектров, а углы дифракции находим из условия главных максимумов 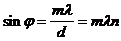 . Для спектра первого порядка jф=11,54o, jкр=20,5o. Для спектра второго порядка jф’=23,6o, jкр’=44,4o. Тогда
. Для спектра первого порядка jф=11,54o, jкр=20,5o. Для спектра второго порядка jф’=23,6o, jкр’=44,4o. Тогда  .
.
Ответы: j1 =20,5o, j2=23,6o, 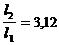
 .
.
Задача 3. Определить ширину дифракционной решетки, которая позволила бы разрешить в спектре третьего порядка две линии натрия с длинами волн 589 нм и 589,6 нм. Постоянная решетки равна 5.10-3 мм.
Дано: m= 3, l1=5,89.10-7 м и l=5,896.10-7 м.
Найти: а –?
Решение. Разрешающая способность решетки  , где
, где  - разность длин волн двух близко расположенных линий. Если максимум одной линии приходится на минимум соседней, эти линии будут видны раздельно, а
- разность длин волн двух близко расположенных линий. Если максимум одной линии приходится на минимум соседней, эти линии будут видны раздельно, а  , где N - число всех щелей.
, где N - число всех щелей.  , так как d - расстояние между соседними щелями.
, так как d - расстояние между соседними щелями.
 . Отсюда
. Отсюда  ; а =1,63.10-3 м=1,63 мм.
; а =1,63.10-3 м=1,63 мм.
Задачи для самостоятельного решения.
8.1. Параллельный пучок монохроматического света с длиной волны 400 нм падает нормально на щель шириной 20 мкм. За щелью помещена линза с фокусным расстоянием 50 см, с помощью которой можно наблюдать дифракционные полосы на экране. Определить расстояние между светлыми полосами первого и второго порядков.
8.2. На щель падает нормально параллельный пучок монохроматического света с длиной волны l. Ширина щели равна 6l. Под каким углом будет наблюдаться третий дифракционный минимум света?
8.3. На непрозрачную пластинку с узой щелью нормально падает монохроматический свет. Угол отклонения лучей, соответствующий второй светлой дифракционной полосе, равен 1о. Скольким длинам волн падающего света равна ширина щели?
8.4. Каково наибольшее значение числа k (номер дифракционного максимума) для желтой линии натрия (l=589 нм) при нормальном падении лучей на щель шириной 2 мкм? Сколько всего наблюдается максимумов?
8.5. На щель шириной 10 мкм нормально падает монохроматический свет с длиной волны l=6.10-7м. Определите значения интенсивностей первого, второго и третьего максимумов, приняв интенсивность нулевого максимума за единицу.
8.6. Монохроматический свет с длиной волны λ = 0.6 мкм падает на длинную прямоугольную щель шириной а = 12 мкм под углом α 0 = 450 к ее нормали. Определите угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума.
8.7. На дифракционную решетку, имеющую 200 штрихов на 1 мм, нормально падает свет от разрядной трубки с водородом. Под каким наименьшим углом дифракции максимумы линий l1=410,2 нм и l2=656,6 нм совпадают.
8.8. На дифракционную решетку длиной l = 15 мм, содержащую N = 3000 штрихов, падает нормально монохроматический свет с длиной волны λ = 550 нм. Определить: 1) число максимумов, наблюдаемых в спектре дифракционной решетки; 2) угол, соответствующий последнему максимуму.
8.9. Определите длину волны монохроматического света, падающего нормально на дифракционную решетку, имеющую 300 штрихов на 1 мм, если угол между направлениями на максимумы первого и второго порядка составляет 120.
8.10. Какой должна была бы быть толщина плоскопараллельной стеклянной пластинки (n = 1,55), чтобы в отраженном свете максимумы второго порядка для λ = 0,65 мнм наблюдался под тем же углом, что и у дифракционной решетки с постоянной d = 1 мкм.
8.11. Как изменится вид дифракционного спектра, если источник белого света, дифракционную решетку и экран (не меняя расстояний между ними) переместить из воздуха в воду? Рассмотрите также случаи, когда для получения дифракционного спектра используется стоящая за дифракционной решеткой собирающая линза
8.12. Две дифракционные решетки имеют одинаковую длину, но разное число штрихов. Как отличаются у этих решеток дисперсии, разрешающие способности?
8.13. В гониометре ГС5 используется дифракционная решетка, имеющая 600 штрихов на 1 мм длины. На каком расстоянии друг от друга будут находиться в фокальной плоскости объектива гониометра с такой решеткой две желтые линии излучения ртутной лампы (λ1= 577нм, λ2 = 589,6нм) в спектре первого порядка, если фокусное расстояние объектива зрительной трубы гониометра 27,3см.
8.14. Ширина решетки 15 мм, период решетки 5 мкм. В спектре какого наименьшего порядка получаются раздельные изображения двух спектральных линий с разностью длин волн 2.10-10 м, если линии принадлежат диапазону крайней красной части видимого спектра (780 нм¸700 нм)?
8.15. На дифракционную решетку нормально падает пучок света от разрядной трубки. Чему должна быть равна постоянная дифракционной решетки, чтобы в направлении j=41о совпадали максимумы двух линий: l1=656,3 нм и l2=4,102 нм?
8.16. Найти наибольший порядок спектра для желтой линии натрия l=589 нм, если постоянная дифракционной решетки равна 2 мкм. Сколько максимумов дает данная решетка?
8.17. Постоянная дифракционной решетки шириной в 2,5 см равна 2 мкм. Какую разность длин волн может разрешить эта решетка в области желтых лучей (l=6.10-5) в спектре второго порядка?
8.18. Угловая дисперсия дифракционной решетки для l=667 нм в спектре первого порядка равна 2,02.105 рад/м. Найти период дифракционной решетки.
8.19. На каком расстоянии друг от друга будут находиться на экране две линии ртутной дуги (l1=577 нм и l2=575,1 нм в спектре первого порядка, полученном при помощи дифракционной решетки с периодом 2.10-4 см? Фокусное расстояние линзы, проектирующей спектр на экране, равно 0,6 м.
8.20. На дифракционную решетку нормально падает пучок света. Красная линия (l=630 нм) видна в спектре третьего порядка под углом j=60о. 1) Какая спектральная линия видна под этим же углом в спектре четвертого порядка? 2) Какое число штрихов на 1 мм длины имеет дифракционная решетка? 3) Чему равна угловая дисперсия этой решетки для линии l=630 нм в спектре третьего порядка?
8.21. Какое фокусное расстояние должна иметь линза. проектирующая на экран спектр, полученный при помощи дифракционной решетки, чтобы расстояние между двумя линиями калия 404,4 нм и 404,7 нм в спектре первого порядка было равно 0,1 мм? Постоянная дифракционной решетки равна 2 мкм.
8.22. На плоскую дифракционную решетку с периодом 5.10-3мм нормально падает пучок монохроматического света. Угол между направлениями лучей, дающих максимумы первого порядка справа и слева от центральной полосы дифракционной картины, равен 13о48’. Определить длину волны падающего света.
8.23. Вычислить наибольший угол, на который может отклониться пучок монохроматического света дифракционной решеткой, имеющей 10 000 штрихов при ширине решетки 4 см. Длина волны падающего света 546 нм. Длина волны падающего света 546 нм. Лучи падают нормально к плоскости решетки.
8.24. Две лампы установлены на расстоянии 20 см друг от друга. С какого расстояния их можно различать в телескопе с диаметром объектива 15 см? Принять, что глаз наиболее чувствителен к длине волны 0,55 мкм.
8.25. Вычислить наибольший разумный диаметр объектива телескопа и наименьшее угловое расстояние между двумя звездами, изображение которых получается раздельно на фотографической пластинке, поставленной в фокальной плоскости объектива телескопа. Фокусное расстояние объектива 2 м. Размер зерна эмульсии фотографической пластинки 0,01 мм. Длина волны света 0,55 мкм.
8.26. Какова должна быть длина дифракционной решетки с периодом 300 штрихов на 1мм, чтобы разрешить две спектральные линии с длинами волн 600нм и 600,05нм в спектре второго порядка? В спектре наивысшего порядка?
8.27. Луч лазера падает на дифракционную решетку перпендикулярно ее плоскости, Отношение х 01: х 12 – расстояний между нулевым и первым (х 01) и между первым и вторым (х 12) дифракционными максимумами на удаленном от решетки экране примерно равно.
8.28. В темной комнате на столе стоит газоразрядная лампа, излучающая вертикальную полоску красного свечения. Если посмотреть на лампу через стеклянную призму спектроскопа отчетливо видны уже три цветные линии: красная, оранжевая и голубая. Далее смотрим на лампу через дифракционную решетку, расположив штрихи решетки вертикально. Что в этом случае можно увидеть? Обоснуйте свои выводы.
ПОЛЯРИЗАЦИЯ СВЕТА
Естественная световая волна - колебания вектора  (напряженности переменного электрического поля) в плоскости, перпендикулярной лучу, изменяют свое направление.
(напряженности переменного электрического поля) в плоскости, перпендикулярной лучу, изменяют свое направление.
Поляризованная световая волна - колебания вектора  в плоскости, перпендикулярной лучу, фиксировано.
в плоскости, перпендикулярной лучу, фиксировано.
Условные обозначения:

Главная плоскость поляризатора (анализатора) – плоскость, в которой колеблется вектор  после прохождения поляризатора (анализатора).
после прохождения поляризатора (анализатора).
Закон Малюса:  ,
,
I 2- интенсивность света за анализатором,
I 1 - интенсивность света после поляризатора,
j - угол между главными плоскостями поляризатора, анализатора.
Формулы Френеля:
 – коэффициент отражения S-колебаний от поверхности диэлектрика;
– коэффициент отражения S-колебаний от поверхности диэлектрика;
 – коэффициент отражения Р-колебаний.
– коэффициент отражения Р-колебаний.
 – коэффициент отражения естественного света. i - угол падения света на поверхность диэлектрика, r - угол преломления.
– коэффициент отражения естественного света. i - угол падения света на поверхность диэлектрика, r - угол преломления.
 – коэффициент отражения естественного света при нормальном падении света на поверхность диэлектрика.
– коэффициент отражения естественного света при нормальном падении света на поверхность диэлектрика.
Закон Брюстера: tg iБ = n 21, iБ + r =p/2.
Угол поворота плоскости поляризации (плоскости колебания вектора  ) света в оптически активных кристаллах: j = a d,
) света в оптически активных кристаллах: j = a d,
где a - удельное вращение, d - толщина слоя кристалла.
Угол поворота плоскости поляризации в растворах: j = a С d,
где С - концентрация оптически активного вещества в растворе.
Угол поворота плоскости поляризации при прохождении света через оптически неактивное вещество, находящееся в однородном магнитном поле индукции В:
j = V d B,
где V - постоянная Верде, d - толщина слоя магнитного поля.
Степень поляризации определяется отношением интенсивности поляризованного света к общей интенсивности света. Для отраженного света  ; для проходящего света
; для проходящего света  , где
, где  - интенсивности в отраженном и проходящем свете для S-колебаний;
- интенсивности в отраженном и проходящем свете для S-колебаний;  - интенсивности в отраженном и проходящем свете для Р-колебаний.
- интенсивности в отраженном и проходящем свете для Р-колебаний.
Примеры решения задач.
Задача 1. Под каким углом должен падать пучок света из воздуха (n1=1) на поверхность жидкости (n2=1,33), чтобы при отражении от дна стеклянного сосуда (n3=1,5), наполненного водой, свет был полностью поляризован?

|
Дано: n1=1, n2=1,33, n3=1,5
Найти: a -?
На границу воздух-вода падает естественный свет под углом a.. Здесь он частично отражается (луч 2) и частично преломляется (луч 3). Лучи 2 и 3 - оба частично поляризованы (в отраженном преобладают S-колебания, в проходящем – Р-колебния). На границе вода-стекло вновь вновь происходит отражение и преломление. При этом отраженный свет полностью поляризован (содержит только S-колебания). А это означает, что угол падения i удовлетворяет закону Брюстера
tg i =  ; tg i =1,5/1,33=1,12, i =48,44о.
; tg i =1,5/1,33=1,12, i =48,44о.
По закону преломления для границы воздух-вода:
 , т.к. n 1=1.
, т.к. n 1=1.
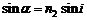 .
.  a =84o.
a =84o.
Ответ: a =84o.
Задача 2. Главные плоскости двух призм Николя образуют между собой угол в 30о. Как изменится интенсивность прошедшего света, если главные плоскости двух николей поставить под углом 45о. Чему равен угол между главными плоскостями двух николей, если после прохождения через них света его интенсивность уменьшилась в 4 раза?
Дано: j1=30o, j2=45o, I ест=4 I 2
Найти: I2’/I2 –? j –?
 Решение. При прохождении света через систему поляризатор–анализатор интенсивность света меняется по закону Малюса
Решение. При прохождении света через систему поляризатор–анализатор интенсивность света меняется по закону Малюса  .
.
Тогда 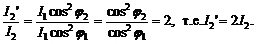 В третьем случае
В третьем случае  . Учтем. что по условию I ест=4 I 2:
. Учтем. что по условию I ест=4 I 2:  . Отсюда
. Отсюда  . Ответы:
. Ответы: 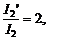
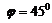 .
.
Задача 3. Естественный свет падает на стекло (n =1,54), под углом полной поляризации. Пренебрегая потерями света, определите: а) коэффициент отражения; б) степень поляризации отраженных лучей и лучей, прошедших в стекло.
 Дано: n =1,54, i=i Б
Дано: n =1,54, i=i Б
Найти: R –? d –? d ’–?
Решение. Коэффициент отражения можно определить, пользуясь формулами Френеля. Тогда
 .
.
По условию i=iБ., т.е. угол полной поляризации, следовательно, угол падения удовлетворяет условию
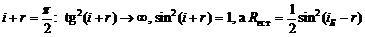 .
.
По закону Брюстера tg iБ = n =1,54, iБ =57o.

Степень поляризации отраженных лучей  , но
, но  . Степень поляризации лучей, прошедших стекло
. Степень поляризации лучей, прошедших стекло  , где
, где
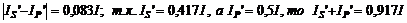 ,
,
 .
.
Задачи для самостоятельной работы.
9.1. Предельный угол полного внутреннего отражения для некоторого вещества равен 45о. Чему равен для этого вещества угол полной поляризации?
9.2. Под каким углом к горизонту должно находиться Солнце, чтобы его лучи, отраженные от поверхности озера, были бы наиболее полно поляризованы?
9.3. Чему равен показатель преломления стекла, если при отражении от него света отраженный луч будет полностью поляризован при угле преломления 30о?
9.4. Пучок естественного света, идущий в воде, отражается от грани алмаза (n=2,42), погруженного в воду. При каком угле падения отраженный свет полностью поляризован?
9.5. Луч света проходит через жидкость, налитую в стеклянный (n=1,5) сосуд, и отражается от дна. Отраженный луч полностью поляризован при падении его на дно сосуда под углом 42о37’. Найти: 1) показатель преломления жидкости, 2) под каким углом должен падать на дно сосуда луч света, идущий в этой жидкости, чтобы наступило полное внутреннее отражение.
9.6. Пучок плоскополяризованного света, длина волны которого в пустоте равна 589 нм, падает на пластинку исландского шпата перпендикулярно его оптической оси. Найти длины волн обыкновенного и необыкновенного лучей в кристалле, если показатели преломления исландского шпата для обыкновенного и для необыкновенного лучей равны соответственно no=1,66 и ne=1,49.
9.7. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивности естественного света, прошедшего через поляризатор и анализатор, уменьшается в четыре раза? Поглощением света пренебречь.
9.8. Луч естественного света проходит сквозь плоскопараллельную стеклянную пластинку (n=1,54), падая на нее под углом полной поляризации. Найти степень поляризации лучей, прошедших сквозь пластинку.
9.9. Определить: 1) коэффициент отражения и степень поляризации отраженных лучей при падении естественного света на стекло (n=1,5) под углом 45о.
9.10. Пластинка кварца толщиной h=1 мм, вырезанная перпендикулярно к оптической оси и помещенная между двумя параллельными николями, поворачивает плоскость поляризации на угол a=20о.При какой толщине кварцевой пластинки свет этой же длины волны не будет выходить из второго николя?
9.11. Какой толщины пластинку кварца нужно поместить между скрещенными николями, чтобы поле зрения стало максимально светлым? Опыт производится в монохроматическом свете (l=500 нм). Удельное вращение кварца для этой длины волны 29,7о на 1 мм.
9.12. Какова концентрация сахара в растворе, если угол поворота плоскости поляризации желтого света при прохождении его через трубку с раствором сахара равен 20о? Длина трубки 15 см. Удельное вращение сахара равно 66,5о дм-1 при концентрации 1 г/см3.
9.13. Определите построением по Гюйгенсу направление преломленных волн и волновые фронты обыкновенного и необыкновенного лучей для случая, когда естественная световая волна падает нормально на грань одноосного кристалла. Оптическая ось кристалла: а) перпендикулярна грани, на которую падает свет; б) параллельна грани, на которую падает свет; в) составляет угол 45о с гранью, на которую падает свет. Построение выполнить для положительного и отрицательного кристаллов.
9.14. Найти построением по Гюйгенсу направления и волновые фронты обыкновенного и необыкновенного лучей, если световая волна падает под углом a к поверхности одноосной кристаллической пластинки, вырезанной под углом 45о к оптической оси. Оптическая ось лежит в плоскости падения.
ОТВЕТЫ
1.1. 1) 1 м, 2) 0,71 м; 1.2. Ф=8,34 лм. 1.3. 2,5 м. 1.4. Когда горит настольная лампа, освещенность края стола больше в 1,2 раза. 1.5. 1) 1,2.107нт, 2) 3.104 нт. 1.6. 520 кд. 1.7. 1,59.108нт. 1.8. Е1/Е2 =1,45. 1.9. 1) 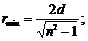 2)
2)  . 1.10. Е2/Е1 =1,6. 1.11. Е1/Е2=ctg α = 5,7. 1.13. t1/t2=2,25 1.14. Е=2×103 лк, R=1,5×103 лм/м2, В=480 кд/м2 1.15. Е≈1,1 (I/ l 2) 1.16. Увеличится в 3 раза. 1.17. 0,5дптр 1.18.
. 1.10. Е2/Е1 =1,6. 1.11. Е1/Е2=ctg α = 5,7. 1.13. t1/t2=2,25 1.14. Е=2×103 лк, R=1,5×103 лм/м2, В=480 кд/м2 1.15. Е≈1,1 (I/ l 2) 1.16. Увеличится в 3 раза. 1.17. 0,5дптр 1.18. 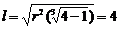 м,где r-расстояние от лампы до центра площадки 1.19. х=1 м. 1.20. а) Е1 /Е2 =4; б) Е1 /Е2 =2. 1.21. Е3 /Е4 =3. 1.22. Е=14,26 лк. 1.23. Е=42 лк. 1.24. 50 см. 1.25. Е1 =61 лк; Е 2=50лк; ∆Е=11 лк.
м,где r-расстояние от лампы до центра площадки 1.19. х=1 м. 1.20. а) Е1 /Е2 =4; б) Е1 /Е2 =2. 1.21. Е3 /Е4 =3. 1.22. Е=14,26 лк. 1.23. Е=42 лк. 1.24. 50 см. 1.25. Е1 =61 лк; Е 2=50лк; ∆Е=11 лк.
2.1. tg i = n. 2.2. 2,02.108 м/с. 2.3. 0,14 м. 2.4. 34о37’ 2.5. 10о8’. 2.6. 1,62 м. 2.7. 1,88. 2.8. A’B’=2 h. 2.9. N1 =3, N2 = 5. 2.10. 7,2 cм. 2.11. Половине роста человека. 2.12. Лучи будут параллельными. 2) Нет. Тоже испытывает полное отражение. 2.13.  . 2.14. a=72о, b=36. 2.15. l =0,58 см 2.16.
. 2.14. a=72о, b=36. 2.15. l =0,58 см 2.16.  2.17. S = 1,88 м. 2.20. 15 см.
2.17. S = 1,88 м. 2.20. 15 см.
2.21. Ðb=600 2.22. 10,2 см 2.23. Длина тени 3,44 м, ширина тени 1,41 м. 2.24. х > 32,3 м. 2.25. j= 770 20’.
3.1. 12 см. 3.2. 120 см. 3.3. Изображение получится в той же точке, где находится источник... 3.7. F=10 см. 3.8. Два изображения в фокусах зеркал, и два на расстоянии (3/2)F от каждого зеркала. 3.9. 3.10. а 2=–12см; у =0,8см 3.11. n=6 3.12. R=24 см. 3.13. d=11,7 см от места, где находилось зеркало 3.14. На расстоянии 30 см от второго зеркала 3.15. l ≈40см. 3.16. k=1,5. 3.17. а) R=1,2; б) R= 2 м, если изображение мнимое. 3.18. F=120 см.
4.1. 1) F1/F2=1,4; 2) В данной жидкости первая линза будет действовать как рассеивающая линза, а вторая как собирающая. 4.2. 1 м. 4.3. F=0,59 м. 4.4. а1 =90 см, а2 =180 см. 4.6. а2 =0,063 м=6,3 см, а2’ =0,24 м=24 см 4.7. F=– 1м. 4.8. 1) l1 =1,36 cм; 2) l2 =0,13 cм; 3) изображение там же, как и при открытой линзе, только освещенность меньше. 4.9. l = a – b. 4.14. F=40 cм. Указание: изображение источника в линзе будет служить источником для зеркала. 4.15. Fo = 0,25 см. 4.16. F2=6 см. 4.17. F=32 мм. 4.18. F=9см 4.19. l = 4см. 4.20. l2/l1=1,1. 4.21. D=7 см. 4.22. А А1=F u2/2Fµg + u2. 4.23.  . 4.24. Sкв/Sизоб=9/16. 4.25. r=4,47 см 4.26. f =22см; H=0,035м 4.27. F1= –15см 4.28. F2=20 см 4.29. х=90 см 4.30. Г=2 4.31. Δd=1см. 4.32.
. 4.24. Sкв/Sизоб=9/16. 4.25. r=4,47 см 4.26. f =22см; H=0,035м 4.27. F1= –15см 4.28. F2=20 см 4.29. х=90 см 4.30. Г=2 4.31. Δd=1см. 4.32. 
5.1. В 1,3. 5.2. у1=1,8 мм, у2=3,6 мм, у3=5,4 мм. 5.3.  =6×10-6 м. 5.4. 5,7.10-7 м. 5.5. 638 нм. 5.6. n хл=1,000865. 5.7. 24,5 см, 32,6 см. 5.8. D l =0,034 см. 5.9. Dj=240о. 5.10. l 1=7,5 мм. 5.11. Δ=3,47 см. 5.12. Δ α=5·10-4 раз. 5.13. 1,2 мм. 5.14. 1 мм. 5.15. Темная полоса.
=6×10-6 м. 5.4. 5,7.10-7 м. 5.5. 638 нм. 5.6. n хл=1,000865. 5.7. 24,5 см, 32,6 см. 5.8. D l =0,034 см. 5.9. Dj=240о. 5.10. l 1=7,5 мм. 5.11. Δ=3,47 см. 5.12. Δ α=5·10-4 раз. 5.13. 1,2 мм. 5.14. 1 мм. 5.15. Темная полоса.
6.1. 1,3×10-7 м. 6.2. 1,9.10-3м. 6.3. N=5 см-1. 6.4. D l2 =0,34 мм.
6.5.  м. 6.6. 0,16 мкм. 6.7. 400 нм. 6.8. 0,181 см. 6.9. В 1,26 раз. 6.10. 11,3 м. 6.11. 119 нм. 6.12. 0,588 мкм. 6.13. Δ х 2=0,3 мм.
м. 6.6. 0,16 мкм. 6.7. 400 нм. 6.8. 0,181 см. 6.9. В 1,26 раз. 6.10. 11,3 м. 6.11. 119 нм. 6.12. 0,588 мкм. 6.13. Δ х 2=0,3 мм.
6.14. n=1,48. 6.15. 998-е кольцо, соответствующее меньшей длине волны. 6.16. d=0,65 мкм. 6.17. D=2,4 дптр, d=1,13 мм. 6.18. F=54 см. 6.19. k=5,6; λ=0,5·10-6м. 6.20. k=275. 6.21. n = 1,000377. 6.22. Прошедший имеет зеленый оттенок, а отраженный – сиреневый оттенок
7.1. а) 3,16 мм; б) 2,24 мм. 7.2. Освещенность уменьшится 7.3. 3 раза. 7.4. r1=0,5 мм; r2= 0,71 мм, r3= 0,86 мм, r4= 1,1 мм, r5= 1, 12 мм. 7.5. r1=0,71 мм; r2= 1 мм, r3= 1,23 мм, r4= 1,42 мм, r5= 1, 59 мм. 7.6. r0=0,8 мм.
8.1. 1 см. 8.2. 30о. 8.3. b»143l. 8.4. k=5; N=11. 8.5. Ij1 =4/(9p2); Ij2 =4/(25p2); Ij3 =4/(49p2). 8.6. α+1=49012¢; α-1 = 4106¢. 8.7. 12о40’. 8.8. 1) n = 18; 2) 81054¢. 8.9. λ=664 нм. 8.10. 577 нм. 8.13. 2,2 мм 8.14. Линии разрешаются в спектре второго порядка. 8.15. 5.10-6 м. 8.16. mmax=3, N=7.
8.17. Dl=0,24.10-10 м.. 8.18. 5.10-6м. 8.19. 0,65 мм. 8.20. 1)l=475 нм,
2) n=460 мм -1. 8.21. 0,63 м. 8.22. 600 нм. 8.23. j =72о50¢ 8.24. 44,7 км.
8.25. D=13,4 см, Dj=1². 8.26. l 1=λ1d/(mΔλ)=2см; mmax≈d/λ=5 l 2=
=λ1d/m maxΔλ=8мм. 8.27. х 01: х 12=1.
9.1. 54°44’. 9.2. 37о. 9.3. n=1,73 9.4. 61°12¢ 9.5. 1) n=1,63, 2) i =66о56’. 9.6. lo=3,55.10-7м, l е =3,95.10-7м. 9.7. a=45о. 9.8. d =18,9 %. 9.9. 1) R=5,06%, d=83%, 2)d’=4,42 %. 9.10.  4,5 мм. 9.11. h=3,02 мм. 9.12. С=0,2 г/см3.
4,5 мм. 9.11. h=3,02 мм. 9.12. С=0,2 г/см3.
СПИСОК ЛИТЕРАТУРЫ
1. Волькенштейн В.С. Сборник задач по физике. - М.: Наука, 2000.
2. Громов С.В. Физика: Молекулярная физика. Квантовая физика. – М.:Просвещение, 1999.
3. Готовцев В.В. Лучшие задачи по оптике и квантовой физике. – М.: ИКЦ «МарТ», Ростов н/Д: Изд. центр «Март», 2004.
4. Иродов И.Е. Задачник по общей физике. - М.: Наука, 1988.
5. Кондратьев А.С., Уздин В.М. Физика. Сборник задач. – М.: Физматлит, 2004.
6. Новодворская Е.М., Дмитриев Э.М. Методика проведения упражнений по физике во втузе. - М.:Высшая школа, 1981.
7. Парфентьева Н.А., Фомина М.В. Правильные решения задач по физике. – М.: Мир, 2001.
8. Савельев И.В. Сборник вопросов и задач по общей физике. - М.: Наука, 1982.
9. Сборник задач по оптике и атомной физике./ Под ред. А.Г. Грамманова -Л.: Изд-во ЛГУ, 1973.
10.Физика: 3800 задач для школьников и поступающих в вузы. – М.: Дрофа, 2000.
12. Чертов А.Г., Воробьев А.А. Задачник по физике. - М.: Физматлит, 2003.
13. Сборник задач по курсу общей физики./ Под ред. М.С.Цедрика – М.: Просвещение, 1989.
ОГЛАВЛЕНИЕ
| Введение | |
| 1. Фотометрия | |
| 2. Отражение и преломление на плоской границе раздела двух прозрачных сред | |
| 3. Сферические зеркала. построение изображений в сферических зеркалах. | |
| 4. Линзы и оптические системы. построение изображений. | |
| 5. Интерференция света. | |
| 6. Интерференция на тонких пленках и пластинках. применение явления интерференции | |
| 7. Дифракция света (Френеля) | |
| 8. Дифракция в параллельных лучах (Фраунгофера) | |
| 9. Поляризация света | |
| Ответы | |
| Список литературы |
| АКУЛИНИНА Александра Васильевна САБИРОВА Файруза Мусовна Задачник-практикум по курсу общей физики. Оптика Учебно-методическое пособие для студентов физико-математического факультета педвуза Технический редактор Сабирова Ф.М. | Договор № ____ Сдано в печать 30.03.04 Формат 84х108/82. Объем 3,7 п.л. Тираж 500 экз. Гарнитура “Таймс” Отпечатано 10.04.2004 г. Типография ЕГПУ Издательство ЕГПУ, 423603, г.Елабуга, ул.Казанская, 89. |
Не нашли, что искали? Воспользуйтесь поиском: