Колебания простейшей одномассовой системы (линейного осциллятора).

Расчетная схема простейшей системы (все массы сосредоточены в одной точке):

Уравнение движения (по 2-му закону Ньютона):

;

где - ускорение, вызванное упругими перемещениям;

- ускорение, вызванное смещением основания;

S_упр - сила упругости (поперечная сила, изгибающий момент не учитывается, т.к. равно нулю угловое ускорение)

S_н.упр - неупругие силы сопротивления - демпфирования.

Закон Гука:

S_упр=-ry,

где r - поперечная сила при единичном упругом смещении:

Для определения неупругих (демпфирующих) сил обычно принимается допущение (гипотеза):

S_н.упр=- .

Подставляя (2), (3) в (1), получим:

, или

.

Уравнение (4) является дифференциальным уравнением колебаний осциллятора при кинематическом возбуждении (сейсмическом воздействии).

При получим дифференциальное уравнение свободных колебаний

;

или

;

где .

Решение уравнения (6):

;

где С и - определяются из начальных условий (при t=0, )

- частота собственных колебаний (с учетом демпфирования), определяемая по формуле:

[1];

где - частота собственных колебаний (без демпфирования), определяемая по расчетной формуле:

.

Вернемся к уравнению (4). Его можно формально трактовать как уравнение вынужденных колебаний под воздействием силы , приложенной к массе М при неподвижном основании:

Воздействие силы Р_(t) можно представить как воздействие на систему суммы элементарных импульсов:

Каждый такой импульс вызывает свободные колебания типа (7) ( t заменяется на ):

.

Просуммируем действие всех элементарных импульсов, т.е. возьмем интеграл от левой и правой частей уравнения (10):

.

В литературе решение (11) носит название интеграла Дюамеля.

Подставим в (11) вместо :

.

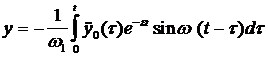Строго говоря, к решению (12) следовало бы добавить решение (7) для свободных колебаний. Однако, главная часть решения - это решение (12), т.к. свободные колебания (см. график), возникнув в первый момент землетрясения, быстро затухают.

Не нашли, что искали? Воспользуйтесь поиском: