Теория метода и описание установки. Математическим маятникомназывается материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебания под действием силы тяжести в одной

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебания под действием силы тяжести в одной вертикальной плоскости.

Таким маятником можно считать тяжелый шарик, подвешенный на тонкой нити, длина 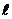которой намного больше размеров шарика.

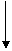
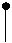
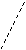
На маятник действуют две силы: сила тяжести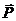

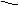и натяжение нити 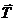. В положении равновесия эти

силы уравновешивают друг друга. Если маятник

отклонить от положения равновесия на угол , то

составляющая силы тяжести

уравновесится натяжением нити Т, другая же

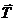
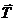составляющая 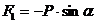, перпендикулярная к

нити, стремится вернуть маятник в положение

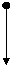
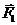равновесия. При малых углах 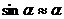, тогда

можно записать, что

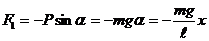, (1)

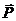
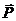
где х – смещение маятника от положения равновесия.

Таким образом, возвращающая сила 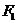пропорциональна смещению , и маятник при малых углах отклонения совершает гармонические колебания.

Возвращающая сила 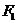подобна упругой силе и ее называют квазиупругой силой.

С другой стороны, силу 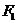можно выразить по второму закону Ньютона:

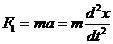(2)

Решая совместно уравнения (1) и (2) получим:

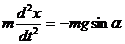или (3)

Из рисунка следует, что 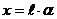, тогда (4)

Подставив выражение (4) в (3), получим

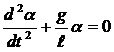
Не нашли, что искали? Воспользуйтесь поиском: