Теория метода и описание установки. Оборотный маятник представляет собой физический маятник.

Оборотный маятник представляет собой физический маятник.

Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси, не проходящей через его центр тяжести. Докажем, что при небольших углах отклонения от положения равновесия физический маятник будет совершать гармонические колебания.

О

С

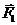
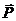
На маятник действует сила тяжести 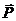, приложенная к его центру тяжести (т. С). Силу тяжести разложим на две составляющие, одна из которых уравновешивается реакцией опоры. Под действием другой составляющей маятник совершает колебания.

Момент этой силы относительно оси, проходящей через точку О равен:

, (1)

где 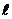- расстояние от оси качания до центра тяжести.

Вращающий момент в соответствии с основным уравнением динамики вращательного движения равен:

, (2)

где - момент инерции маятника;

- угловое ускорение.

Приравнивая правые части уравнений (1) и (2), получим:

или, так как угол мал, ,

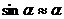(3)

Уравнение (3) является дифференциальным уравнением колебаний физического маятника. Сравнив это уравнение (3) с дифференциальным уравнением гармонических колебаний , видим, что если заменить на и обозначить , то они совпадают.

Т.е. физический маятник совершает гармонические колебания, и период Т колебаний его можно определить по формуле:

, (4)

где - момент инерции маятника относительно оси качания;

- масса маятника.

Величину называют приведенной длиной физического маятника. Под приведенной длиной физического маятника понимают длину такого математического маятника, период колебаний которого равен периоду колебаний физического маятника.

Момент инерции маятника относительно оси качания можно выразить по теореме Штейнера:

, (5)

где - момент инерции маятника относительно оси, проходящей через центр тяжести.

Подставив (5) в (4), получим:

(6)

Прибор состоит из горизонтальной планки, прикрепленной к стене. Наверху планки находится подушка ножевых опор для установки физического маятника.

Оборотный маятник представляет собой цилиндрический стержень, на котором закреплены две треугольные ножевые опоры (опорные призмы 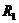и 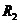) и две массивные чечевицы и , которые можно смещать.

Подвешивая маятник поочередно на призмы 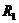и ,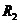

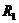найдем периоды колебани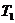й и :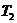

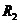
Выполним математические преобразования:

Вычтем из первого уравнение второе:

Отсюда найдем ускорение силы тяжести :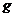

Так как - расстояние между опорными призмами, последнюю формулу можно переписать в виде:

(7)

Не нашли, что искали? Воспользуйтесь поиском: