
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Затухающие колебания
Краткая теория
Колебательным движением называется всякое движение или изменение состояния, характеризуемое той или иной степенью повторяемости во времени значений физических величин, определяющих это движение или состояние. Колебания свойственны всем явлениям природы: пульсирует излучение звезд; с высокой степенью периодичности вращаются планеты Солнечной системы; ветры возбуждают колебания и волны на поверхности воды; внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы, например, с удивительной надежностью бьется человеческое сердце.
В физике выделяются колебания механические и электромагнитные. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большое число прямой информации об окружающем мире. Примерами колебательного движения в механике могут быть колебания маятников, струн, мостов и т.д.
Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Простейшим типом периодических колебаний являются гармонические колебания. Гармоническими называются колебания, при которых изменение колеблющейся величины со временем происходит по закону синуса (или косинуса):
 , (1)
, (1)
где x – смещение от положение равновесия;
А – амплитуда колебания – максимальное смещение от положения равновесия;
 - циклическая частота;
- циклическая частота;
 - начальная фаза колебания;
- начальная фаза колебания;
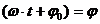 - фаза колебания; она определяет смещение в любой момент времени, т.е. определяет состояние колебательной системы.
- фаза колебания; она определяет смещение в любой момент времени, т.е. определяет состояние колебательной системы.
В случае строго гармонических колебаний величины А,  и
и  не зависят от времени.
не зависят от времени.
Циклическая частота  связана с периодом Т колебаний и частотой
связана с периодом Т колебаний и частотой  соотношением:
соотношением:
 (2)
(2)
Периодом Т колебаний называется наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебания.
Частотой 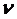 колебаний называется число полных колебаний, совершаемых за единицу времени, измеряется в герцах (1 Гц = 1
колебаний называется число полных колебаний, совершаемых за единицу времени, измеряется в герцах (1 Гц = 1  ).
).
Циклическая частота  численно равна числу колебаний, совершаемых за 2
численно равна числу колебаний, совершаемых за 2  секунд.
секунд.
Колебания, возникающее в системе, не подверженной действию переменных внешних сил, в результате какого-либо начального отклонения этой системы от состояния устойчивого равновесия, называются свободными (или собственными).
Если система консервативная, то при колебаниях не происходит рассеяния энергии. В этом случае свободные колебания называются незатухающими.
Скорость  колебания точки определим как производную от смещения по времени:
колебания точки определим как производную от смещения по времени:
 (3)
(3)
Ускорение  колеблющейся точки равно производной от скорости по времени:
колеблющейся точки равно производной от скорости по времени:
 (4)
(4)
Уравнение (4) показывает, что ускорение при гармонических колебаниях – переменно, следовательно, колебание обусловлено действием переменной силы.
Второй закон Ньютона позволяет в общем виде записать связь между силой F и ускорением  при прямолинейных гармонических колебаниях материальной точки с массой
при прямолинейных гармонических колебаниях материальной точки с массой  :
:
 , (5)
, (5)
где  , (6)
, (6)
к – коэффициент упругости.
Таким образом, сила, вызывающая гармонические колебания, пропорциональна смещению и направлена против смещения. В связи с этим можно дать динамическое определение гармонического колебания: гармоническим называется колебание, вызываемое силой, прямо пропорциональной смещению х и направленной против смещения.
Возвращающей силой может быть, например, сила упругости. Силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие условию (5), называются квазиупругими.
В случае прямолинейных колебаний вдоль оси х ускорение  равно:
равно:
 .
.
Подставив это выражение для ускорения  и значение силы
и значение силы 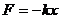 во второй закон Ньютона, получим основное уравнение прямолинейных гармонических колебиний:
во второй закон Ньютона, получим основное уравнение прямолинейных гармонических колебиний:
 или
или  (7)
(7)
Решением этого уравнения является уравнение (1).
Затухающие колебания
Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания затухают – их амплитуда постепенно уменьшается.
При небольших скоростях движения силы, вызывающее затухание колебаний, пропорциональны величине скорости  . Эти силы называют силами сопротивления (трения):
. Эти силы называют силами сопротивления (трения):
 , (8)
, (8)
где  - коэффициент сопротивления.
- коэффициент сопротивления.
Знак минус указывает, что сила сопротивления всегда направлена в сторону, противоположную направлению движения.
Запишем второй закон Ньютона для затухающих прямолинейных колебаний тела:
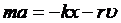 или
или  (9)
(9)
Решив это дифференциальное уравнение, получим уравнение затухающих колебаний материальной точки:
 , (10)
, (10)
где  - амплитуда затухающего колебания;
- амплитуда затухающего колебания;
 - амплитуда в начальный момент времени (
- амплитуда в начальный момент времени ( =0);
=0);
 - основание натуральных логарифмов;
- основание натуральных логарифмов;
 - коэффициент затухания, связанный с коэффициентом сопротивления
- коэффициент затухания, связанный с коэффициентом сопротивления  и массой
и массой  соотношением:
соотношением:
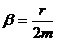 (11)
(11)
Скорость затухания колебаний оценивается величиной  , которая называется логарифмическим декрементом затухания.
, которая называется логарифмическим декрементом затухания.
Логарифмический декремент затухания  равен натуральному логарифму отношения амплитуд колебаний, следующих друг за другом через промежуток времени, равный периоду Т:
равен натуральному логарифму отношения амплитуд колебаний, следующих друг за другом через промежуток времени, равный периоду Т:
 (12)
(12)
Выясним физический смысл величин  и
и  . Пусть за время
. Пусть за время  амплитуда колебаний уменьшается в
амплитуда колебаний уменьшается в  раз. Тогда
раз. Тогда  , отсюда
, отсюда 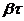 = 1 или
= 1 или  .
.
Следовательно, коэффициент затухания  есть физическая величина, обратная промежутку времени
есть физическая величина, обратная промежутку времени  , в течение которого амплитуда уменьшается в
, в течение которого амплитуда уменьшается в  раз.
раз.
Пусть N – число колебаний, после которых амплитуда уменьшается в  раз.
раз.
Тогда 

Следовательно, логарифмический декремент затухания  есть физическая величина, обратная числу колебаний
есть физическая величина, обратная числу колебаний  , по истечении которых амплитуда уменьшается в
, по истечении которых амплитуда уменьшается в  раз.
раз.
Механические волны
Если в упругую среду поместить колеблющееся тело (источник колебаний), то соседние с ним частицы среды тоже придут в колебательное движение. Колебания этих частиц передается силами упругости соседним частицам среды и т.д. Через некоторое время колебание охватит всю среду. Процесс распространения колебаний в среде называется волной. Основное свойство всех волн, независимо от их природы, состоит в том, что в волне осуществляется перенос энергии без переноса вещества.
Волны могут различаться по тому, как возмущения ориентированы относительно направления их распространения. Если колебания частиц происходят в том же направлении, что и распространение энергии, волны называются продольными. Если же колебания частиц перпендикулярны к направлению распространения энергии, то такие волны называются поперечными. Продольные волны образуются в результате деформаций сжатия или растяжения. Поперечные волны возникают при деформациях сдвига. В твердых телах упругие силы возникают при деформациях растяжения, сжатия и сдвига, поэтому в твердых телах могут возникать как продольные, так и поперечные волны. В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому в газах и жидкостях механические волны могут быть только продольными.
Уравнение волны – это уравнение, позволяющее определить смещение любой точки волны в любой момент времени.
Пусть источником колебания является точка О, колеблющаяся гармонически по закону:

Все частицы среды придут в гармоническое колебание с такой же частотой и амплитудой, но с различными фазами. В среде возникает волна.
Тогда уравнение колебания частицы В, находящейся на расстоянии  от источника колебания (т. О) запишется:
от источника колебания (т. О) запишется:
 , (1)
, (1)
где  - время распространения колебаний от т. О до т. В, т.е. время, за которое волна проходит путь
- время распространения колебаний от т. О до т. В, т.е. время, за которое волна проходит путь  .
.
 , где
, где  - скорость распространения волны.
- скорость распространения волны.
Тогда уравнение (1) можно переписать:
 |
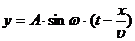 (2)
(2)
Уравнение (2), позволяющее определить смещение любой точки волны в любой момент времени, является уравнением волны.
Основными характеристиками волн являются:
длина волны  - эторасстояние между двумя ближайшими точками волны, находящимися в одинаковой фазе, например, между двумя максимумами или минимумами возмущения;
- эторасстояние между двумя ближайшими точками волны, находящимися в одинаковой фазе, например, между двумя максимумами или минимумами возмущения;
период волны Т – время, за которое совершается один полный цикл колебания.
Длина волны  связана с периодом Т соотношением:
связана с периодом Т соотношением:
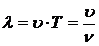 , (3)
, (3)
где  - скорость распространения волны;
- скорость распространения волны;
 - частота волны.
- частота волны.
Подставляя выражение (3) в (2) и учитывая, что 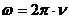 , получим другие формулы уравнения волны:
, получим другие формулы уравнения волны:


Выражение  называется фазой волны. Разность фаз колебаний двух точек среды, расстояние между которыми
называется фазой волны. Разность фаз колебаний двух точек среды, расстояние между которыми 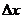 равна:
равна:

В точках, отстоящих друг от друга на целое число длин волн 
 , разность фаз составляет четное число
, разность фаз составляет четное число 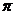
 , т.е. колебания в этих точках протекают в одинаковой фазе – синфазно.
, т.е. колебания в этих точках протекают в одинаковой фазе – синфазно.
В точках, отстоящих друг от друга на нечетное число длин полуволн, т.е. для которых 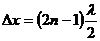 , где
, где  =1,2,…, разность фаз равна нечетному числу
=1,2,…, разность фаз равна нечетному числу 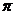 , т.е.
, т.е.  . Колебания в таких точках происходят в противофазе: в то время, как отклонение в одной равно А, в другой оно равно –А и наоборот.
. Колебания в таких точках происходят в противофазе: в то время, как отклонение в одной равно А, в другой оно равно –А и наоборот.
Интерференция волн
Если в данную точку среды приходят две волны, то их действие складывается. Особо важное значение имеет сложение когерентных волн. Когерентными называются волны, имеющие постоянную во времени разность фаз.
Интерференция волн – это сложение в пространстве когерентных волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны. В результате получается интерференционная картина в виде чередующихся максимумов и минимумов.
В точках, куда обе волны приходят в фазе, они усиливают друг друга, т.е.
если  (1)
(1)
В точках, куда обе волны приходят в противофазе, они ослабляют друг друга:
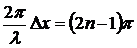 (2)
(2)
Условия максимума (1) и минимума (2) можно еще записать и так:
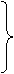
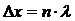
(3)

Разность  называется разностью хода волн. Следовательно, усиление (максимум) будет наблюдаться при интерференции, если разность хода волн равна целому числу длин волн; если разность хода составляет нечетное число длин полуволн, будет наблюдаться ослабление (минимум).
называется разностью хода волн. Следовательно, усиление (максимум) будет наблюдаться при интерференции, если разность хода волн равна целому числу длин волн; если разность хода составляет нечетное число длин полуволн, будет наблюдаться ослабление (минимум).
Стоячие волны
Важным случаем интерференции волн является сложение двух когерентных волн, движущихся навстречу друг другу вдоль одной прямой. При наложении этих волн возникает стоячая волна – периодическое во времени синфазное колебание с характерным пространственным распределением амплитуды – чередованием узлов и пучностей.
Стоячая волна может быть получена, если прямая волна, посланная вибратором к препятствию, наложится на отраженную от него волну. Уравнение стоячей волны получим сложением уравнения прямой волны

и уравнения отраженной волны, движущейся в направлении противоположном прямой волне
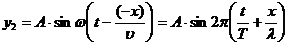
Смещение точки, участвующей одновременно в двух колебаниях, равно:

Из тригонометрии известно, что 
Поэтому окончательно получим уравнение стоячей волны:
 , (1)
, (1)
где  =
=  - амплитуда стоячей волны, зависит от координаты точки х. Иными словами, амплитуды колебания различных точек различны.
- амплитуда стоячей волны, зависит от координаты точки х. Иными словами, амплитуды колебания различных точек различны.
Точки, в которых амплитуда максимальная, называются пучностями (точки 1,3,5).
Точки, в которых амплитуда равна нулю, в колебании не участвуют и называются узлами (точки 2,4,6)



 У
У 
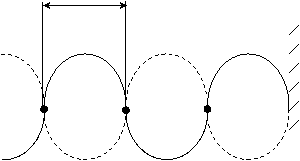 |
1 2 3 4 5 6
 | |||
 | |||
 |
Расстояние между соседними узлами (или пучностями) называется длиной стоячей волны:
 ,
,
где  - длина бегущих волн.
- длина бегущих волн.
В отличие от бегущей волны в стоячей волне не происходит переноса энергии, а осуществляется лишь пространственная перекачка энергии одного вида в энергию другого вида.
Не нашли, что искали? Воспользуйтесь поиском: