НА ОСНОВЕ СЧЕТЧИКОВ ДЖОНСОНА

Кольцевой регистр с перекрестной обратной связью (счетчик Джонсона, счетчик Мебиуса, счетчик Либау-Крейга) обладает обратной связью замкнутой на первый триггер от инверсии выходного сигнала (рис.15, а) [1]. Он имеет состояний, то есть при той же разрядности вдвое больше, чем обычный кольцевой регистр. В то же время выход счетчика Джонсона представлен не в коде «1 из N», что требует преобразования кодов для получения выходов распределителя тактов. Такие преобразователи очень просты, что и обуславливает применение счетчиков Джонсона в составе распределителей [1].

Показанный на рис. 15, а четырехразрядный счетчик Джонсона при начальном нулевом состоянии работает следующим образом. Первый тактовый импульс «Сдвиг» установит первый триггер в единичное состояние , так как , в остальных разрядах будут нули как результат сдвига нулей от соседних слева разрядов. Второй импульс «Сдвиг» сохраняет единичное состояние первого триггера, так как по-прежнему . Второй же разряд окажется в единичном состоянии , поскольку примет единицу от первого триггера. Остальные разряды будут нулевыми. Последующие сдвиги приведут к заполнению единицами всех разрядов счетчика, то есть «волна единиц», распространяясь слева направо, приведет счетчик в состояние «1111». Следующий импульс сдвига установит первый разряд в нуль, так как теперь . Этим начинается процесс распространения «волны нулей». После восьми импульсов повторится состояние «0000», с которого было начато рассмотрение работы счетчика. Временные диаграммы описанных процессов показаны на рис.15, б.

Рис.15. Схема счетчика Джонсона (а) и временные диаграммы его работы (б)

Особенность рассмотренной схемы – четное число состояний при любом n (2 n – всегда число четное). Обычный кольцевой регистр такого ограничения не имеет.

Преобразование выходного кода счетчика Джонсона в код «1 из N» требует добавления всего одного двухвходового элемента «И» либо «И-НЕ» для каждого выхода распределителя тактов. Принцип дешифрации состоит в выявлении положения характерной координаты временной диаграммы – границы между зонами единиц и нулей (табл. 3).

Таблица 3

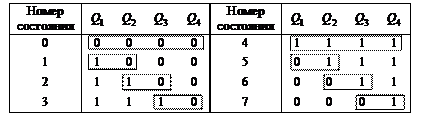
В двух случаях (для слов, состоящих только из нулей или только из единиц) состояние выявляется анализом крайних разрядов. В остальных случаях анализируются разряды на границе зоны единиц и нулей.

Как видно из таблицы, преобразование выходного кода счетчика Джонсона в код «1 из N» осуществляется согласно выражениям

где – выходы распределителя тактов.

По полученным выражениям строится дешифратор. Рассмотрим дешифратор с элементами «И-НЕ» (с инверсными выходами). В таком дешифраторе можно дополнительно принять меры по предотвращению перекрытий импульсов в соседних каналах, возможных из-за различных задержек элементов. Используя элементы с тремя входами и «косыми связями» (рис.16, а), можно запретить начало импульса в последующем канале до его завершения в предыдущем.

Распределитель тактов в целом (рис.16, б) имеет выходные сигналы в коде «1 из N».

Для схем со счетчиками Джонсона могут возникнуть вопросы преодоления ограничения обязательной четности числа состояний счетчика и обеспечения автоматического вхождения его в рабочий цикл (свойства самозапуска).

Первую задачу можно решить в рамках подхода, применявшегося при построении счетчиков с произвольным модулем, то есть исключением одного «лишнего» состояния.

Рис.16. Схемы преобразования кода Джонсона в коде «1 из N» (а) и распределителя на основе счетчика Джонсона (б)

Получить схему с исключенным состоянием можно показанным выше способом, переходя от таблицы функционирования к функциям возбуждения триггеров и далее к схеме. Однако в данном случае нетрудно сократить этот путь, пользуясь простыми рассуждениями. Пусть исключению подлежит состояние «11...11». Чтобы его исключить, нужно перейти к следующему состоянию не от состояния «все единицы», а от предыдущего состояния «11...10», которое создает единицу в предпоследнем разряде счетчика, то есть нуль на инверсном выходе этого разряда. Подавая этот нулевой сигнал на вход счетчика вместе с основным сигналом обратной связи через конъюнктор (показан на рис.16, б штриховой линией), исключим состояние «11...11» и получим счетчик с нечетным числом состояний .

Задача обеспечения вхождения распределителя на основе счетчика Джонсона в рабочий цикл связана с тем, что базовая схема, рассмотренная ранее, свойством самозапуска не обладает. Например, распределитель с трехразрядным счетчиком Джонсона имеет общее число возможных состояний , а число состояний в рабочем цикле . Неиспользуемыми являются два состояния: «010» и «101». Нетрудно видеть, что из состояния «010» счетчик перейдет в состояние «101», а из состояния «101» в состояние «010». Таким образом, наряду с замкнутым рабочим циклом существует и замкнутый цикл из двух неиспользуемых состояний, попав в который, схема без постороннего воздействия не сможет перейти в рабочий цикл.

Чтобы придать схеме свойство самозапуска, нужно модифицировать сигнал обратной связи, поступающий на вход счетчика. Понятно, что это можно сделать многими путями, поскольку траектория перехода из замкнутого цикла неиспользуемых состояний в рабочий неоднозначна. Одной из возможностей является выработка сигнала обратной связи согласно выражению

Распределители на основе счетчиков Джонсона характеризуются небольшими аппаратными затратами (1/2 триггера и один двухвходовой вентиль на канал) и достаточно высоким быстродействием (время установления равно сумме задержек переключения триггера и вентиля). Счетчики Джонсона реализованы, в частности, в сериях элементов типа КМОП (микросхемы ИЕ9 и ИЕ19 серии К561 и др.), причем одной из причин их применения является отсутствие импульсов помех в выходном напряжении и пониженный уровень токовых импульсов в цепях питания, создаваемых микросхемами. Распределитель в целом реализован в виде интегральной схемы К561ИЕ8.

Следует заметить, что распределители могут быть получены без применения специализированных схем в виде сочетания обычного двоичного счетчика и дешифратора. Это решение наиболее очевидно. Однако такая схема имеет ряд недостатков. Одним из них является искажение выходной последовательности в результате возникновения гонок. Выходом из этой ситуации может служить синтез синхронного распределителя импульсов по приведенному ниже алгоритму [3]. Рассмотрим эту процедуру на конкретном примере. Пусть необходимо построить схему, формирующую две выходные последовательности и (рис. 17).

Рис. 17. Выходные последовательности распределителя

Алгоритм синтеза распределителя импульсов (РИ) может быть представлен следующим образом:

1. Определить величину одного кванта времени D как наибольший общий делитель (НОД) из длительностей импульсов и интервалов между ними для всех выходов .

: 40, 20, 30, 20 (мс);

: 20, 20, 20, 30 (мс).

Из исходных данных получаем:

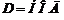
D = НОД(, ) = НОД(40, 20, 30, 20, 20, 20, 20, 30) = 10 (мс)

2. Импульсные последовательности разбить на отрезки величиной D. Для каждого j -го отрезка записать код вида

, где m – количество выходов РИ.

Среди m выходных последовательностей не должно быть взаимно инверсных, поскольку такие последовательности получаются автоматически (на инверсных выходах элементов памяти или с использованием дополнительного инвертора).

В рассматриваемом примере получаются следующие коды:

: «11», «11», «11», «10», «00», «01», «11», «10», «00», «00».

3. В множестве кодов вида необходимо подсчитать максимальное число k одинаковых кодов, если одинаковых кодов нет, то следует перейти к п. 6.

В нашем примере чаще всего повторяется код «11», k = 4.

4. Определить общее количество элементов памяти n по формуле

, где 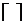– знак округления до ближайшего справа целого числа. Для рассматриваемого примера .

5. Доопределить m -разрядные коды до n -разрядных таким образом, чтобы среди них не было одинаковых:

: «0011», «0111», «1011», «0010», «0000», «0001», «1111», «0110», «0100», «1000».

6. Используя аппарат синтеза счетчиков с произвольным порядком счета, построить требуемый РИ.

При большом числе выходных каналов эта структура может выигрывать у других, но при малом числе каналов преимущество по аппаратной сложности и быстродействию, как правило, оказывается на стороне вариантов с кольцевыми регистрами или счетчиками Джонсона.

Не нашли, что искали? Воспользуйтесь поиском: