Дніпропетровський національний університет залізничного транспорту імені академіка В. Лазаряна 3 страница

У прикладі за заданим законом обертального руху тіла D треба визначити лінійні швидкості точки М обода диска і тіла С (рис. 16).

Закон обертального руху тіла - це закон зміни за часом кута повороту тіла φ = φ(t).Маючи таку інформацію, визначимо кутову швидкість диска як похідну за часом від закону руху диска:

Оскільки кутова швидкість залежить від часу, знайдемо її значення в заданий момент часу с: рад/с.

Далі через знайдену кутову швидкість визначимо лінійну швидкість точки М як точки, що належить тілу, яке обертається. Вона дорівнює добутку кутової швидкості диска D на відстань від точки М до осі обертання диска:

м/с.

Щоб визначити швидкість тіла С (як точки) треба врахувати, що воно зв’язане з точками обода диска D меншого радіуса за допомогою троса, що не розтягується; тому швидкість тіла С буде дорівнювати лінійній швидкості будь-якої точки цього обода, розташованої на відстані від осі обертання диска:

0,8·0,2 = 0,16 м/с.

Примітка. Відомо, що швидкості точок тіла, яке обертається, пропорційні їх відстаням до осі обертання. Так як швидкості точок обода диска з радіусом R дорівнюють швидкості тіла А, а швидкості точок обода диска з радіусом r дорівнюють швидкості тіла С, то швидкість V_C можна знайти ще із такого співвідношення:

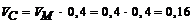м/с.

Таким чином, із наведених у прикладі відповідей правильною буде відповідь 1).

Приклад 2. Вказати правильну відповідь.

Якщо кутова швидкість диска B (рис. 17) змінюється за законом ω = – 0,3 t² + 0,9 t (рад/c), а відстань ОМ = м, то в заданий момент часу сшвидкість таприскорення точки M диска будуть мати такі значення:

1) V_М = 0,7 м/с; a_М = 0,234 м/с²;

2) V_М = 0,3 м/с; a_М = 0,372 м/с²;

3) V_М = 0,3 м/с; a_М = 0,234 м/с²;

4) V_М = 0,7 м/с; a_М = 0,372 м/с².

Розв’язан ня. У даному прикладі за заданим законом зміни кутової швидкості диска В ω = ω (t) треба визначити швидкість та прискорення точки М диска в заданий момент часу t₁ = 2с.

Оскільки точка М – це точка тіла, яке обертається навколо нерухомої осі, то лінійні кінематичні характеристики руху точки (V_М, a_М) без затруднень визначаються через кутові кінематичні характеристики обертального руху тіла (ω, ε).

Так, лінійна швидкість визначається за формулою V_M = w ×OM = w ×R, де кутова швидкість ω в заданий момент часу має значення:

рад/с.

Тоді м/с.

Оскільки в процесі обертання диска рух точки М відбувається по круговій кривій радіуса ОМ = R (рух точки криволінійний), то її повне прискорення буде складатися із двох взаємно перпендикулярних складових векторів – тангенціального і нормального прискорень: .

Тангенціальне прискорення визначається через кутове прискорення εза формулою , а нормальне прискорення – через кутову швидкість ω: . Величина ж повного прискорення обчислюється за формулою: .

Визначимо кутове прискорення диска як похідну за часом від закону зміни кутової швидкості:

Чисельне значення кутового прискорення в заданий момент часу t₁ = 2 c становить: рад/с².

Тоді складові вектори повного прискорення і повне прискорення точки М у заданий момент часу t₁ = 2 с набувають таких значень:

м/с²;

м/с²;

м/с².

Отже, із наведених у прикладі відповідей правильною буде відповідь 3).

Примітка. Треба зауважити, що в прикладі 2 кутова швидкість диска в заданий момент часу t₁= 2c приймає додатне значення, а кутове прискорення – від ’ ємне значення, тобтоω і εмають різні знаки. Це означає, що обертальний рух тіла буде уповільненим. Але цей рух не можна назвати рівноуповільненим,оскільки кутове прискорення тіла залежить від часу, тобто не є сталою величиною (e ¹ const).

Приклад 3. Вказати правильну відповідь.

Якщо в механічній системі (рис. 18) тіло A рухається відповідно до закону

S_A = 0,2 t² + 0,3 t (м),

а радіуси ступінчастого диска B становлять м, м, то в заданий момент часу скутове прискорення диска B та лінійне прискорення тіла С набувають таких значень:

1) ε = 2,0 рад/с²; a_С = 1,40 м/с²;

2) ε = 1,8 рад/с²; a_С = 0,72 м/с²;

3) ε = 2,0 рад/с²; a_С = 0,80 м/с² ;

4) ε = 1,8 рад/с²; a_С = 1,40 м/с².

Розв’язання. У даному прикладі за заданим законом руху тіла А треба визначити кутове прискорення диска та лінійне прискорення тіла С в заданий момент часу с.

Оскільки тіло А в процесі переміщення системи виконує поступальний рух, то далі його будемо розглядати як точку. Закон руху тіла А дозволяє визначити його тангенціальне прискорення. Воно дорівнює другій похідній за часом від закону руху, або першій похідній від закону зміни швидкості:

; ;

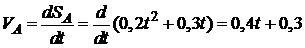м/с².

Слід зауважити, що точки обода диска меншого радіуса зв’язані з тілом А тросом, який не розтягується, тому вони мають за значенням такі ж самі швидкості і, відповідно, тангенціальні прискорення, як і тіло А. Тоді, враховуючи співвідношення , можна знайти кутове прискорення ε за формулою:

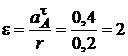рад/с².

Повне прискорення тіла C (як точки) буде складатися з двох складових векторів – тангенціального і нормального прискорення: , а величина повного прискорення буде обчислюватися за формулою:

.

Слід зауважити, що тіло С зв’язано тросом, який не розтягується, з точками обода диска більшого радіуса. Тому тіло С має за значенням таке ж тангенціальне прискорення, як і точки обода диска. Тоді величину можна підрахувати за формулою: м/с².

Величина нормального прискорення відповідає формулі: , де ρ_C -

радіус кривизни траєкторії тіла C (як точки), який дорівнює нескінченності, бо рух точки відбувається по прямій. Тому нормальне прискорення в цьому випадку відсутнє: 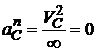. Тоді повне прискорення тіла C дорівнює тангенціальній складовій і його значення становить: м/с².

Таким чином, із наведених у прикладі відповідей правильною буде відповідь 3).

Приклад 4. Вказати правильну відповідь. Обчислення проводити з точністю до трьох значущих цифр.

Якщо в механічній системі (рис. 19) ступінчастий диск D обертається відповідно до закону φ = 0,6 t² − 0,2 t (рад),

а його радіуси мають значення м, м, то в заданий момент часу 1 с повне прискорення точки М диска і прискорення тіла C мають значення:

1) a_М = 0,595 м/с²; a_С = 0,24 м/с²;

2) a_М = 0,624 м/с²; a_С = 0,32 м/с²;

3) a_М = 0,595 м/с²; a_М = 0,32 м/с²;

4) a_М = 0,624 м/с²; a_С = 0,24 м/с².

Розв’язання. У даному прикладі розглядається рух системи, що складається з двох тіл - С і D. Тіло С виконує поступальний рух, тому далі під час розрахунків будемо розглядати його як точку. Тіло D виконуєобертальний рух навколо нерухомої осі, що спрямована перпендикулярно до площини малюнка і проходить через точку О (рис. 19). Це тілоє ступінчастим диском, для якого в умові прикладу задаються значення радіусів - R, r.

Тут за заданим законом обертального руху тіла D треба визначити лінійні прискорення точки М обода диска і тіла С.

Знаючи закон обертального руху диска D, можна визначити його кутову швидкість і кутове прискорення:

;

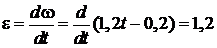рад/с².

Так як кутова швидкість залежить від часу, знайдемо її значення в заданий момент часу с: рад/с.

Далі через знайдену кутову швидкість і кутове прискорення диска визначимо нормальне, тангенціальне і повне прискорення точки М, що знаходиться на ободі диска.

Оскільки у процесі обертання диска рух точки М відбувається по круговій кривій радіуса ОМ = R (рух точки криволінійний), то її повне прискорення буде складатися із двох взаємно перпендикулярних складових векторів – тангенціального і нормального прискорень: .

Тангенціальне прискорення точки М визначається через кутове прискорення диска ε за формулою м/с², а нормальне прискорення – через кутову швидкість дискаω:

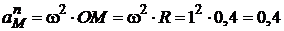м/с² .

Величина ж повного прискорення точки становить:

м/с².

Тіло С зв’язано з диском тросом, який намотано на обід меншого радіуса.

Рух тіла С, як точки, прямолінійний (відбувається по вертикалі). Тому слід зауважити, що нормальне прискорення тіла С, як точки, буде дорівнювати нулю: 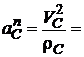, де ρ _C - радіус кривизни прямої.

Тоді повне прискорення тіла С буде дорівнювати тангенціальній складовій; а вона набуває такого ж значення, як і тангенціальне прискорення будь-якої точки обода диска меншого радіуса. Тобто

м/с².

Отже, із наведених у прикладі відповідей правильною буде відповідь 4).

Приклад 5. Вказати правильну відповідь.

Якщо тіло A механічної системи (рис. 20) рухається відповідно до закону

S_A= − 0,1 t² + 0,8 t (м),

то напрямки кутової швидкості і кутового прискорення диска, прискорення тіла А і точки M диска в момент часу t₁ = 2 cбудуть такими:

1) 2) 3)

Розв’язання. В даному прикладі за заданим законом руху тіла А треба визначити напрямок кутового прискорення диска і напрямки лінійних прискорень тіла А та точки М диска в заданий момент часу t₁ = 2 с.

Оскільки тіло А в процесі переміщення системи виконує поступальний рух, то далі його будемо розглядати як точку. Закон руху тіла А дозволяє визначити його швидкість і тангенціальне прискорення та, найголовніше, встановити їх знаки. Треба зауважити, що згідно з рис. 20 додатний напрямок відліку відповідає додатним значенням координати S_A, які відкладаються донизу.

Швидкість тіла А, як точки, дорівнює похідній за часом від його закону руху, а тангенціальне прискорення цього тіла дорівнює похідній за часом від закону зміни швидкості:

;

м/с² < 0.

Значення швидкості тіла А в заданий момент часу t₁ = 2 с становить:

м/с > 0.

Наведені результати свідчать про те, що швидкість тіла А приймає додатне значення, а його тангенціальне прискорення − від’ємне. Це означає, що вектор швидкості спрямований у додатному напрямку відліку координат S_A – униз, а вектор тангенціального прискорення спрямований у від’ємному напрямку відліку – уверх. Тоді кутова швидкість диска відповідно до формули (де r – радіус диска), має знак швидкості і спрямована у бік , тобто в даному випадку проти годинникової стрілки; а кутове прискорення відповідно до формулі має знак тангенціального прискорення 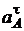і спрямоване у бік цього вектора, в даному випадку - за годинниковою стрілкою.

Нормальне прискорення тіла А, як точки, дорівнює нулю, так як рух його прямолінійний, а повне прискорення цього тіла дорівнює тангенціальній складовій і спрямоване уверх (як і тангенціальне прискорення).

Напрямок тангенціального прискорення точки М відповідає напрямку e, а її нормальне прискорення завжди спрямоване до центра кривизни траєкторії, тобто до осі обертання.

Отже, із наведених у прикладі відповідей правильною буде відповідь 2).

2.3. Динаміка

2.3.1. Динаміка точки

Приклад 1. Вказати правильну відповідь. Обчислення проводити з точністю до трьох значущих цифр.

Якщо сила ваги тіла А (рис. 21) маєзначення 100 H (P = 100 H),сила тяги 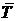і сила тертя відповідно становлять 15 H і 5 H(T = 15 H, = 5 H), то тіло будерухатися вздовж осі з прискоренням:

1) а = 2,0 м/с²;

2) а = 4,0 м/с²;

3) а = 6,0 м/с²;

4) а = 8,0 м/с².

Розв’язання. У даному прикладі розглядається рух тіла А униз по нахиленій площині, розташованої під кутом 30° до горизонту. Треба визначити прискорення тіла А, якщо відомі усі сили, що діють на нього під час руху.

Оскільки тіло А в процесі переміщення виконує поступальний рух, то далі його будемо розглядати як точку.

Щоб відповісти на питання прикладу, треба скористатися основним рівнянням динаміки точки

.

Для отримання чисельних результатів це векторне рівняння треба записати у скалярному вигляді, тобто в проекціях на координатні осі. Так як рух тіла А, як точки, прямолінійний, то достатньо це рівняння спроектувати на напрямок руху, тобто на задану вісь x:

;

тут прискорення точки проектується на вісь x в натуральну величину − , а сума проекцій усіх сил на вісь x становить:

= T + P·sin30 − = 15 + 100·0,5 − 5 = 60 Н.

Масу точки визначимо через силу ваги за формулою кг.

Тоді рівняння динаміки буде мати такий вигляд: . Звідси прискорення тіла А, як точки, дорівнює: 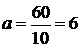м/с².

Таким чином, правильною тут буде відповідь 3).

Приклад 2. Вказати правильну відповідь.

На заданому переміщенні S_A (рис. 22) від’ємну роботу (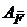 < 0) виконує:

1) сила ;

2) сила ;

3) сила .

Розв’язання. У даному прикладі розглядається рух тіла А вверх по нахиленій площині, що розташована під кутом β до горизонту. Треба визначити, яка з трьох сил, що діє на тіло під час руху, виконує від’ємну роботу на переміщенні S_A цього тіла.

Щоб відповісти на питання прикладу, треба скористатися загальною формулою для обчислення роботи сили, яка має такий вигляд:

.

Тут F − модуль (величина) сили, S − переміщення точки прикладення сили, α − кут між напрямком сили і напрямком переміщення. Із формули випливає, що знак роботи дає множник 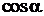. Якщо кут α гострий (α < 90 ⁰), то значення косинуса цього кута додатне і робота сили додатна (+); якщо кут α тупий (α > 90 ⁰), то значення косинуса кута від’ємне і робота сили від’ємна (–); якщо ж кут α прямий (α = 90 ⁰; сила перпендикулярна до переміщення), то значення косинуса кута дорівнює нулю і робота сили дорівнює нулю.

У даному випадку тупий кут з напрямком переміщення S_A утворює сила , так як α = 90 ⁰ + . Оскільки косинус тупого кута від’ємний, то сила буде виконувати від’ємну роботу.

Отже, із наведених у прикладі відповідей правильною буде відповідь 3).

Примітка.Із загальної формули для обчислення роботи сили випливає ознака, що допомагає визначити без розрахунків знак роботи:якщо сила прискорює рух точки (тіла), то робота її додатна(+); якщо уповільнює – то від’ємна (–); якщо ж сила не впливає на рух (не прискорює його і не уповільнює), то робота її дорівнює нулю.

У даному прикладі прискорює рух тіла сила , бо спрямована вона у бік руху ( = 0; 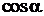= 1) і робота її додатна; уповільнює рух тіла сила (вона гальмує рух тіла уверх по площині) і робота її від’ємна; не впливає на рух тіла сила (не прискорює рух і не уповільнює його), тому робота її дорівнює нулю ( = 90⁰, 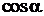= 0; сила перпендикулярна до переміщення S_A).

2.3.2. Динаміка твердого тіла та системи тіл

Приклад 1. Вказати правильну відповідь.

Якщо на диск (рис. 23) масою m = 10 кг і радіусом R = 0,4 м діє момент сил опору М_оп = 2 Н·м, то обертальний рух диска відбувається з кутовим прискоренням, яке за абсолютним значенням становить:

1) | ε | = 1,8 рад/с²;

2) | ε | = 2,5 рад/с²;

3) | ε | = 1,5 рад/с²;

4) | ε | = 3,6 рад/с².

Розв’язання. Щоб відповісти на питання прикладу, треба скористатися основним рівнянням динаміки обертального руху тіла навколо нерухомої осі:

Тут I_z – момент інерції тіла відносно осі обертання z, що спрямована в даному випадку перпендикулярно до площини малюнка і проходить через центр мас диска – точку С; ε – кутове прискорення тіла; – сума моментів усіх сил, що діють на тіло, відносно осі обертання. Тоді кутове прискорення тіла визначається за формулою:

До суми моментів усіх сил відносно осі обертання надходить лише момент сил опору, так як інші сили, що діють на тіло в процесі руху (сила ваги , сили , 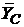– складові реакції нерухомого шарніра C), моментів відносно осі обертання не створюють, бо перетинають цю вісь (проходять через вісь):

Формула для обчислення I_z – моменту інерції суцільного однорідного диска відносно центральної осі, має вигляд:

де m – маса диска; R – його радіус.

Підставимо дані в наведені формули і отримаємо чисельний результат:

Н·м; к г · м²;

рад/с².

Отже, із наведених у прикладі відповідей правильною буде відповідь 2).

Приклад 2. Вказати правильну відповідь.

Якщо механічна система (рис. 24) складається із вантажів А масою m_А = 10 кг та D масою m_D = 4 кг і ступінчастого диску В з радіусом інерції ρ_В = 0,4м (R_В = 0,5 м; r_В = 0,2м) і масою m_В = 5 кг, то при значенні швидкості тіла А V_A = 2 м/c кінетична енергія системи дорівнює:

1) Т ^сист = 100 Dж;

2) Т ^сист = 110 Dж;

3) Т ^сист = 120 Dж;

4) Т ^сист = 130 Dж.

Розв’язання. У даному прикладі розглядається рух механічної системи, що складається із трьох тіл (тіла А, В і D),зв’язаних між собою тросами. У процесі переміщення системи ці троси не розтягуються. Треба визначити кінетичну енергію заданої системи у тому її положенні, коли швидкість тіла А набуває значення V_A = 2 м/c.

Кінетична енергія системи дорівнює арифметичній сумі кінетичних енергій усіх тіл і точок системи і в даному випадку становить:

Не нашли, что искали? Воспользуйтесь поиском: