КРИТЕРИИ РАБОТОСПОСОБНОСТИ ЗУБЧАТЫХ ПЕРЕДАЧ

МЕТОДИЧЕСКОЕ УКАЗАНИЕ

К практическим занятиям по дисциплине

«Детали машин и основы конструирования» и «Прикладная механика» для студентов специальностей НР-090600; НРГ-090602; НРК-090603; СТХ-090702; НТХ-090703; НБ-090800; МОП-170299; МХП-170500; МКС-120200; ТМ-120100; МиМ-120800; ТПП-271200; АТХ-150200; СТЭ-230100; ЭАТ-240100; ПДМ-170900; СП-120500 ПМб-553300; ГФН – 080200; ГН – 080500, ГИГ – 011400, Дизайн – 152400 очной и заочной форм обучения.

Тюмень 2004

Утверждено редакционно-издательским советом

Тюменского государственного нефтегазового университета

СОСТАВИТЕЛИ: д.т.н., проф. А.А. Тарасенко,

к.т.н., доцент А.П. Школенко,

к.т.н., доцент К.В. Сызранцева,

к.т.н., доцент В.А. Сапухин,

ассистент С.Ю. Михайлов.

© государственное образовательное учреждение высшего профессионального образования

«Тюменский государственный нефтегазовый университет» 2004 г.

ВВЕДЕНИЕ.

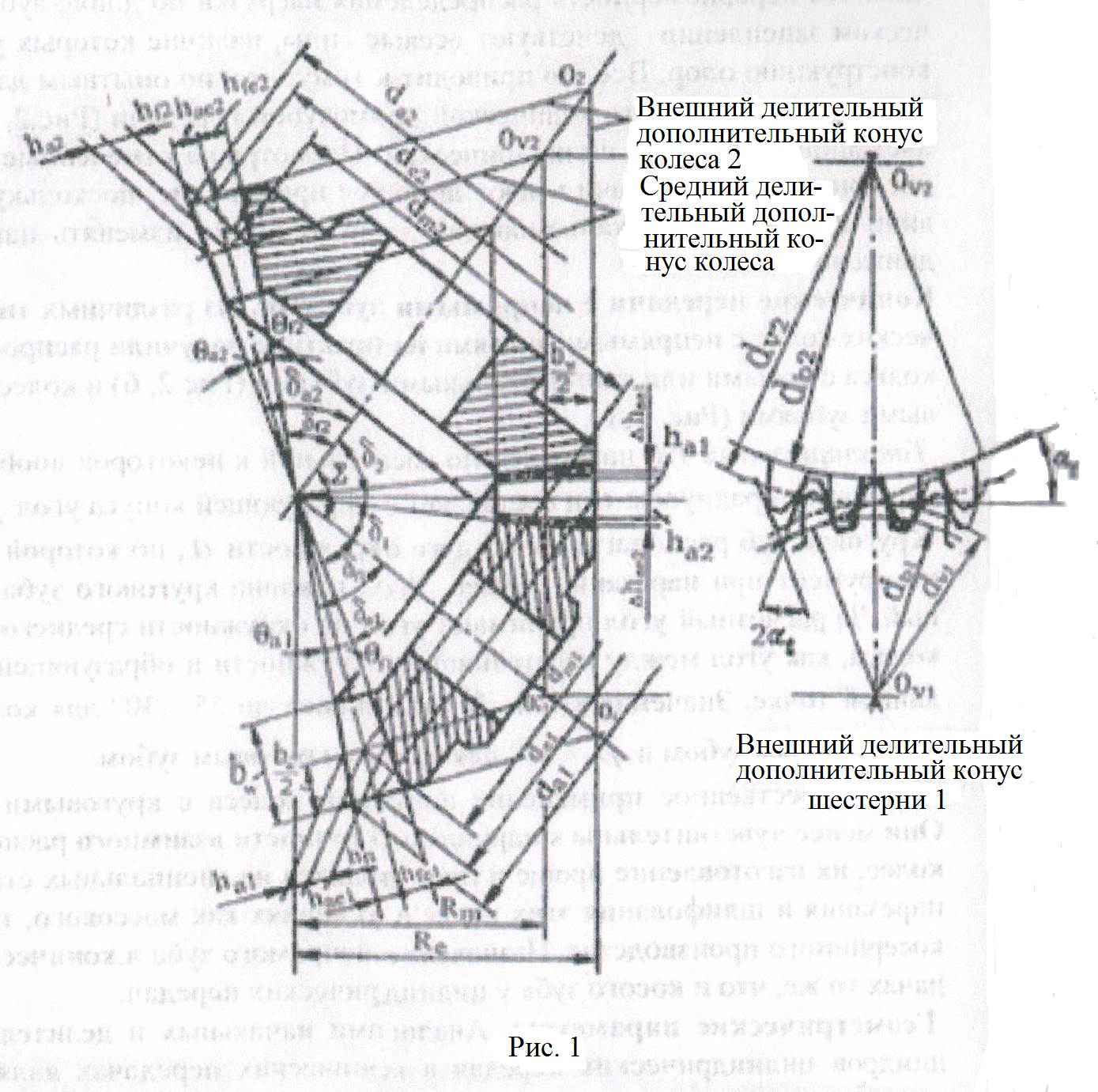
Общие сведения и характеристика. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом Σ (рис. 1). Наиболее распространены передачи с углом Σ = 90º.

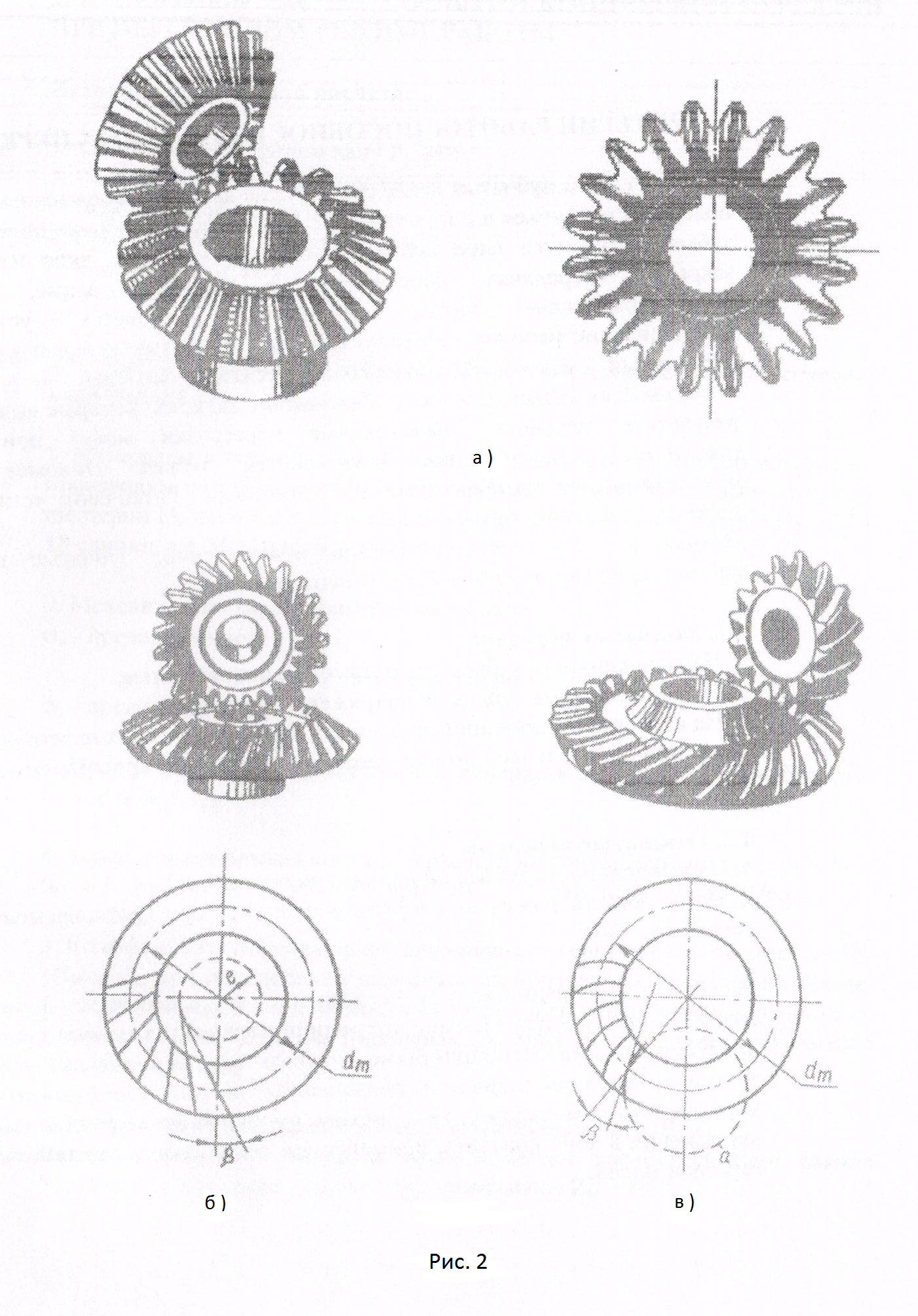
Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и специальный инструмент. Кроме допусков на размеры зубьев здесь необходимо выдерживать допуски на углы Σ, δ₁ и δ₂ (рис. 1), а при монтаже обеспечивать совпадение вершин конусов. Выполнить коническое зацепление с той же степенью точности, что и цилиндрическое, значительно труднее. Пересечение осей валов затрудняет замещение опор. Одно из конических колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузке по длине зуба. В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все то приводит к тому, что, по опытным данным, погрузочная способность конической прямозубой передачи (Рис. 2, а) составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, конические передачи имеют широкое применение, поскольку по условиям компоновки механизмов иногда необходимо изменять направление движения.

Конические передачи с непрямыми зубьями. Из различных типов конических колес с непрямыми зубьями на практике получили распространение колеса с косыми или тангенциальными зубьями (Рис. 2, б) и колеса с круговыми зубьями (Рис. 2, в).

Тангенциальный зуб направлен по касательной к некоторой воображаемой окружности радиусом е и составляет с образующей конуса угол β.

Круговой зуб располагается по дуге окружности a, покоторой движется инструмент при нарезании зубьев. Угол наклона кругового зуба переменный. За расчетный угол принимают угол на окружности среднего диаметра колеса, как угол между касательной к окружности и образующей конуса в данной точке. Значения углов β выполняют до 25…30º для колес с тангенциальным зубом и β ≈ 35º для колес с круговым зубом.

Преимущественное применение получили колеса с круговыми зубьями. Они менее чувствительны к нарушению точности взаимного расположения колес, их изготовление проще и производится на специальных станках для нарезания и шлифования этих колес в условиях как массоого, так и мелкосерийного производства. Назначение непрямого зуба в конических передачах то же, что и у косого зуба у цилиндрических передач.

Геометрические параметры. Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами δ₁, δ₂ (рис.1). При коэффициентах смещения инструмента x₁ + x₂ = 0 начальные и делительные конусы совпадают. Конусы, образующие которых перпендикулярны образующим делительных конусов, называют дополнительными делительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е, например d_e, R_m и др.; R_e и R_m – внешнее и среднее конусные расстояния, b – ширина зубчатого венца.

Размеры по внешнему торцу удобнее для измерения, их используют на чертежах. Размеры в среднем сечении используют при силовых расчетах.

КРИТЕРИИ РАБОТОСПОСОБНОСТИ ЗУБЧАТЫХ ПЕРЕДАЧ

Выход из строя зубчатых колёс связан чаще всего с повреждением рабочих поверхностей зубьев и с их поломкой. Повреждение рабочих поверхностей зубьев вызывается либо контактными напряжениями, либо износом. В закрытых передачах, работающих в масляной ванне, наиболее распространенным видом повреждения является усталостное выкрашивание рабочих поверхностей. Для открытых передач характерен абразивный износ. У высоконагруженных передач на рабочих поверхностях зубьев возможно образование задиров, которые возникают в результате заедания. Значительные перегрузки могут привести к пластической деформации поверхностей зубьев. Поломка зубьев обуславливается изгибающими напряжениями. Различают усталостную поломку и поломку от перегрузок.

Исходя из перечисленных видов повреждений, зубчатые передачи рассчитывают на прочность следующим образом.

Закрытые передачи.

1. На выносливость зубьев по контактным напряжениям;

2. На выносливость зубьев по напряжениям изгиба;

3. На контактную прочность зубьев при кратковременных перегрузках;

4. На прочность зубьев по напряжениям изгиба при кратковременных перегрузках.

Открытые передачи

1. На выносливость зубьев по напряжениям изгиба;

2. На прочность зубьев по напряжениям изгиба при кратковременных перезагрузках.

Расчеты на износостойкость и заедание до настоящего времени не разработаны. Предупреждение чрезмерного износа и заедания достигается конструктивными мероприятиями, такими как термическая обработка зубьев до высокой твёрдости, повышением чистоты поверхности зубьев, коррегированием зацепления с целью уменьшения скорости взаимного скольжения в зоне контакта, применением специальных противозадирных смазок и масел.

2. ПРОЕКТНЫЙ РАСЧЁТ ЗАКРЫТОЙ КОНИЧЕСКОЙ ПЕРЕДАЧИ ПРИ ПЕРЕМЕННОМ РЕЖИМЕ РАБОТЫ

Исходные данные расчёта:

1. Мощность на ведущем валу P₁, кВт;

2. Частота вращения ведущего вала n₁, об/мин;

3. Передаточное число U;

4. Срок службы передачи L, годы;

5. Режим нагружения.

2.1. Выбор материалов зубчатых колёс и определение допускаемых напряжений.

1. Материалы и термическая обработка зубчатых колёс. Выбор материалов производим по таблице 1. Прил. Для лучшей приработки зубьев твёрдость шестерни H₁ рекомендуется назначать больше твёрдости колеса H₂ на 10-15 единиц, т.е. H₁ = H₂ + (10…15)HB

2. Механические характеристики материала

σ_в (предел прочности) и σ_т (предел текучести) выбираются по таблице 1.Прил.

3. Предел контактной выносливости поверхности зубьев σ_Hlim, выбирается по таблице 1.Прил.

4. Коэффициент безопасности при расчёте на контактную прочность S_H:

S_H = 1,1 при HRC ≤ 35; S_H = 1,2 при HRC > 35 или по таблице 1.Прил.

5. Коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев Z_R при определении допускаемых контактных напряжений. Значение Z_R принимают в зависимости от класса шероховатости поверхности по таблице 2.Прил. Для быстроходных передач рекомендуется принимать большие значения.

6. Коэффициент, учитывающий окружную скорость колёс Z_V:

Величину окружной скорости колёс в начале расчёта считают равной 5…10 м/с, а для скоростей v ≤ 5 м/с принимают Z_V = 1,0.

7. Число оборотов работы передачи L_h за расчетный срок службы:

L_h = L ∙ 365K_год ∙ 24K_сут (1)

Где K_год и K_сут – коэффициенты использования передачи в году и сутках.

8. Коэффициент долговечности при расчёте на контактную выносливость K_HL.:

K_HL = , причем 1 ≤ K_HL ≤ 2,4 (2)

Если K_HL < 1, то принимать K_HL =1,0.

N_HO – базовое число циклов перемен напряжений, определяется в зависимости от твёрдости по Бринелю или Роквеллу по формуле:

N_HO = 30(HB)^2,4 ≈ 0,063 (HRC)² + 8 ∙ 10⁶. (3)

Для материалов, твердость которых задана по Бринелю, N_HO может быть определено по графику рисунка 7.Прил.

При постоянном режиме нагружения число циклов перемен напряжений:

N_HE = 60 ∙ L_h ∙ n ∙ c, (4)

Где L_h – число работы передачи за расчётный срок службы в часах;

n – частота вращения того из колёс, по материалу которого определяется допускаемое напряжение;

с – число зацеплений зуба за один оборот колеса.

При переменных режимах нагружения, заданных циклограммой:

N_HE = 60 ∙ L_h ∙ c ∙ Σ ∙ 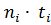(5)

Где T_i – крутящие моменты, которые учитывают при расчёте;

T_max – максимальный из моментов, участвующих в расчёте;

n_i; t_i – соответствующие моментам Т частоты вращения и время работы.

9. Допускаемые контактные напряжения [σ_H]₁ и [σ_H]₂, МПа:

[σ_H] = 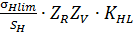, (6)

Для прямозубых передач, а также для косозубых, у которых твёрдость зубьев шестерни и колеса различаются незначительно, за расчётное допускаемое напряжение принимается меньшее из допускаемых напряжений, определённых для материала шестерни [σ_H]₁ и колеса [σ_H]_2.

Остальных случаях допускаемое напряжение определяют:

[σ_H] = (7)

10. Предел выносливости зубьев по напряжениям изгиба σ_Flim, определяется по таблице 1.Прил.

11. Коэффициент безопасности при расчёте на изгиб S_F:

S_F = 1,55 … 1,75 по таблице 1.Прил.

12. Коэффициент, учитывающий шероховатость переходной поверхности при расчете допускаемых напряжений изгиба Y_R:

Y_R = 1,0 для фрезерованных и шлифованных зубьев;

Y_R = 1,2 для полированных зубьев.

13. Коэффициент, учитывающий влияние двухстороннего приложения нагрузки K_FC:

K_FC = 0,65 для улучшенных сталей;

K_FC = 0,75 для закалённых сталей;

K_FC = 0,90 для цементированных сталей.

При одностороннем приложении нагрузки K_FC = 1,0.

14. Коэффициент долговечности при расчёте на изгиб K_FL:

K_FL = 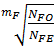, причем 1 ≤ K_FL ≤ 2. (8)

Если K_FL < 1, то принимать K_FL = 1,0.

N_FO – базовое число циклов перемен напряжений.

Для всех сталей N_FO = 4∙10⁶;

N_FЕ – эквивалентное число циклов нагружений.

При переменных режимах нагружения заданных циклограммой:

N_FE = 60 ∙ L_h ∙ c ∙ Σ 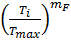∙ 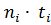(9)

m_F = 6 при HRC ≤ 50 или HB ≤ 350;

m_F = 9 при HRC > 50 или HB > 350.

15. Допускаемые напряжения изгиба [σ_F]₁ и [σ_F]₂ , Мпа:

[σ_F] = 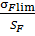∙ Y_R ∙ K_FL ∙ K_FC. (10)

16. Предельные допускаемые контактные напряжения при кратковременных перегрузках [σ_H]_max1 и [σ_H]_max2, Мпа:

[σ_H]_max = 2,8 ∙ σ_Т. (11)

Данная формула приведена для нормализованных, улучшенных и объемно закаленных зубьев (σ_Т – предел текучести материала – по табл. 1.Прил.)

[σ_H]_max = 40 ∙ HRC (12)

Данная формула приведена для цементованных, азотированных и т.в.ч. закаленных зубьев.

17. Предельные допускаемые напряжения изгиба при кратковременных перегрузках [σ_F]_max1 и [σ_F]_max2, МПа:

[σ_F]_max = 0,8 ∙ σ_Т, при HB ≤ 350; (13)

[σ_F]_max = 0,6 ∙ σ_B, при HB < 350. (14)

(σ_B – предел прочности материала – по таблице 1.Прил.)

Проектный расчет.

Проводится с целью определения геометрических параметров зубчатых колес исходя из условия обеспечения их контактной прочности.

18. Крутящий момент на выходном валу T₂, Н ∙ м:

T₂ = T₁ ∙ U ∙ η, (15)

Где T₁ – крутящий момент на ведущем валу, Н ∙ м: T₁ = P₁ / ω₁;

ω₁ – угловая скорость ведущего вала, с^-1: ω₁ = πn₁/30;

η – коэффициент полезного действия зубчатой конической передачи (η = 0,96…0,98).

19. Приведенный модуль упругости E_пр:

E_пр = 2,1 ∙ 10⁵ МПа – для обоих зубчатых колес стальных;

E_пр = 1 ∙ 10⁵ МПа – для обоих зубчатых колес чугунных;

E_пр = 1,36 ∙ 10⁵ МПа – для стальной шестерни и чугунного колеса;

E_пр = (0,135 … 0,154) ∙ 10⁵ МПа – для стальной шестерни и текстолитового колеса.

20. Коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии в результате погрешностей в зацеплении и деформации зубьев K_Hβ (по рисунку 8.Прил.).

21. Коэффициент ширины зубчатого венца относительно внешнего конусного расстояния K_be:

K_be ≤ 0,3 – меньшие значения для неприрабатывающихся материалов (Н1 и Н2 > 350 НВ или υ > 15 м/сек). Наиболее распространено значение K_be = 0,285.

22. Опытный коэффициент ϑ_Н, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической. (По таблице 3. Прил.)

Для прямозубой передачи -ϑ_Н = 0,85.

23. Диаметр внешней делительной окружности колеса, мм:

d_e2 = 2,9 ∙ 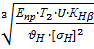. (16)

Величину d_e2 округляют до стандартного значения по таблице 4. Прил. Следует предпочитать первый ряд. Фактические значения d_e2 не должны отличаться от номинальных более чем на 2%.

24. Диаметр внешней длительной окружности шестерни, мм:

d_e1 = . (17)

25. Углы делительных конусов, º:

- колеса δ₁ = arctg ; (18)

- шестерни δ₂ = 90 - δ₁ (19)

26. Внешнее конусное расстоияние, мм:

R_e = . (20)

27. Ширина зубчатых колес, мм:

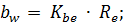(21)

Округляем ширину зубчатых колес 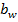по таблице 5. Прил.

28. Среднее конусное расстояние, мм:

R_m = R_e – 0,5 ∙ b_w. (22)

29. Диаметры средних делительных окружностей шестерни d_m1 и колёса d_m2, мм:

d_m1 = d_e1 – b_w ∙ sin δ₁; (23)

d_m2 = d_e2 – b_w ∙ sin δ₂; (24)

30. Определение числа зубьев шестерни Z₁:

- определяется по графикам рисунка 9. Прил.;

По значению определяют:

Z₁ = 1,6 ∙ , при H₁ и H₂ ≤ 350 HB, (25)

Z₁ = 1,3 ∙ , при H₁ ≥ 45 HRC и H₂ ≤ 350 HB, (26)

Z₁ = , при H₁ и H₂ ≥ 45 HRC. (27)

Округлить найденное значение Z₁ до целого числа.

31. Число зубьев колеса:

Z₂ = Z₁ ∙ U (28)

Округлить найденное значение Z₂ до целого числа.

32. Фактическое передаточное число U:

U = 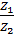. (29)

Фактическое передаточное число не должно отличаться от стандартного более чем на 2,5% при U 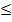4,5 и на 4,0% при U > 4,5.

33. Внешний окружной делительный модуль m_te, мм:

Для конических зубчатых колес с прямыми зубьями в качестве стандартного расчетного модуля принимают внешний окружной делительный модуль: m_te = m_e.

m_te = (30)

m_te округляется до стандартных значений по таблице 6. Прил.

34. Внешний нормальный делительный модуль m_e, мм:

Для конических зубчатых колес с тангенциальными (косыми) зубьями в качестве стандартного расчетного модуля зубьев принимают внешний нормальный делительный модуль m_e:

m_e = m_te ∙ cos β. (31)

35. Средний нормальный модуль m_tm, мм:

В передачах с круговым зубом расчет ведут по среднему нормальному подулю m_tm:

m_tm = cos β ∙ m_te 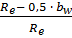. (32)

36. Диаметры окружностей выступов шестерни d_a1 и колеса d_a2, мм:

для прямозубых передач:

d_a1 = d_e1 + 2 ∙ m_te ∙ cos δ₁; (33)

d_a2 = d_e2 + 2 ∙ m_te ∙ cos δ₂. (34)

для косозубых передач:

d_a1 = d_e1 + 2 ∙ m_e ∙ cos δ₁; (35)

d_a1 = d_e1 + 2 ∙ m_e ∙ cos δ₁. (36)

для передач с круговым зубом:

d_a1 = d_e1 + 2 ∙ m_tm ∙ cos δ₁; (37)

d_a1 = d_e1 + 2 ∙ m_tm ∙ cos δ₁. (38)

37. Диаметры окружностей впадин шестерни d_fe1 и колеса d_fe2, мм:

для прямозубых передач:

d_fe1 = d_e1 - 2,4 ∙ m_te ∙ cos δ₁; (39)

d_fe1 = d_e1 - 2,4 ∙ m_te ∙ cos δ₁. (40)

для косозубых передач:

d_je1 = d_e1 – 2,4 ∙ m_e ∙ cos δ_1; (41)

d_je2 = d_e2 – 2,4 ∙ m_e ∙ cos δ_2. (42)

для передач с круговым зубом:

d_je1 = d_e1 – 2,4 ∙ m_tm ∙ cos δ₁; (43)

d_je2 = d_e2 – 2,4 ∙ m_tm ∙ cos δ₂. (44)

38. Определяем среднюю окружную скорость, м/с:

υ_ср = 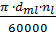. (45)

39. Выбор степени точности:

Степень точности определяем в зависимости от средней окружной скорости, по табл 7.Прил.

2.3. Расчет сил действующих в зацеплении (Силы, действующие в зацеплении, представлены на рис.3):

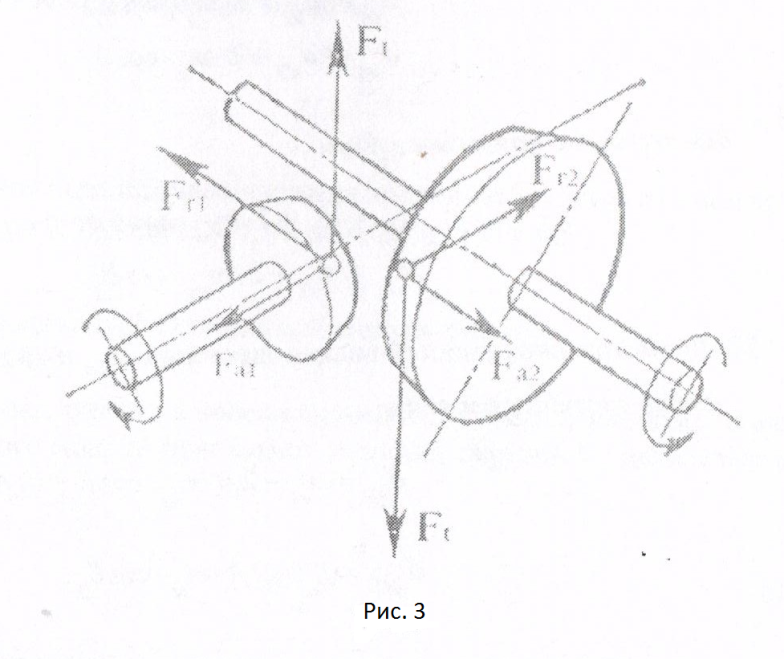
Для прямозубых колес:

40. Окружная сила F_t, H:

F_t = . (46)

41. Радиальная сила для шестерни F_rl, равная осевой силе для колеса F_a2, Н:

F_r1 = F_a2 = F_t ∙ tg α ∙ cos δ₁. (47)

42. Осевая сила для шестерни F_a1, равная радиальной силе для колеса F_r2, Н:

F_a1 = F_r2 = F_t ∙ tg α ∙ sin δ₁. (48)

где α – угол зацепления. Для некоррегированных зубчатых колёс α = 20º.

Для колес с непрямыми зубьями:

43. Окружная сила F_t, H:

F_t = 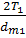. (49)

44. Радиальная сила для шестерни F_r1 , равная осевой силе для колеса F_a2, Н:

F_r1 = F_a2 ∙ 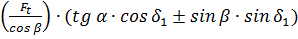. (50)

45. Осевая сила для шестерни F_a1, равная радиальной силе для колеса F_r2, H:

F_a1 = F_r2 ∙ 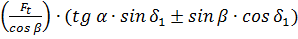. (51)

В последних формулах знак зависит от направления внешнего момента, приложенного к валу шестерни, и линии наклона зуба как винтовой линии. Верхние знаки – направления момента (при наблюдении с торца) и винтовые линии зуба – совпадают, нижние не совпадают. Значение углов наклона β выполняют до 25…30º для колес с тангенциальным (косым) зубом и β ≈ 35º для колес с круговым зубом. (рис.2).

Не нашли, что искали? Воспользуйтесь поиском: