Метод Б. П. Хохлова и Л. Л. Еремина

⇐ Предыдущая 98 99 100 101 102103104 105 106 107 Следующая ⇒

Имея грунтмодель исходного размера, рас-четно-графическим путем получают грунт-модели одного или обоих крайних размеров серии. Вписав грунтмодель исходного размера в оси координат так, чтобы ее длина совпадала с осью ОХ (рис. VIII.3, а), отрезок ОН на оси ОХ, равный длине грунтмодели, делят на равные части (число отрезков может быть от 16 до 20 и более) с помощью циркуля для пропорционального деления или дополнительной линии HD (H'D'), которая без остатка делится на выбранное число отрезков.

Определив расчетным путем длину грунт-модели крайнего размера L _гр.кри отложив ее на оси О'Х' (рис. VIII. 3, б), делят ее длину на то же число отрезков, что и исходную. Через намеченные точки перпендикулярно осям ОХ и О'Х' проводят линии и нумеруют каждую в одинаковом порядке на исходном и крайнем размерах.

Для построения поперечных размеров применяется градировочный треугольник (рис. VIII. 3, в), построение которого отличается от его построения по методу ЕДМО, но основано на той же пропорциональности поперечных размеров деталей основному широтному параметру колодки — обхвату ее в пучках (сеч. 0,72/0,68 L). Ниже рассмотрено построение равнобедренного градировочного треугольника.

Рис. VIII. 3. Схема построения грунтмодели крайнего размера для заготовок объемного и пространственного типа: а — исходный размер; б — искомый размер; в — градировочный треугольник

Основание равнобедренного треугольника АБВ равно ¹ / ₂ О_пуч исходного размера, высота БЕ в 1,5 раза больше основания. Продлив основание треугольника в сторону от точки В, от точки А откладывают расстояние, равное ¹ / ₂ О_пуч крайнего размера, определяемое по государственному стандарту на колодки (для искомого, т. е. крайнего, размера и выбранной полноты). Отрезок БД является абсолютным приращением половины обхвата пучков для п размеров:

ВД= ± ¹ / ₂ ΔО _пуч п.

При градировании модели по метрической системе нумерации с 240 по 275 размер 4-й полноты отрезок БД равен + 10,5 мм.

Из вершины треугольника через точку Д проводят линию крайнего большего размера основного широтного параметра колодки, а через точку Г — линия крайнего меньшего:

ВД= – ¹ / ₂ ΔО _пуч п

Для градирования деталей, поперечные размеры которых больше основания АБ, продолжают стороны треугольника и линии БД и БГ вниз (например, до линии аб). Градировочный треугольник обычно строят на миллиметровой бумаге, наклеивают на бумагу ватман и не вырезают по контуру.

При градировании на исходной грунтмодели (см. рис. VIII.3, а) измерителем или циркулем замеряют расстояние (1"—1, 2" —2, 3"—3 и т. д.) от контура деталей модели до оси ОХ. Затем среди линий на градировочном треугольнике между сторонами БА и БВ находят равную измеренной и замеряют расстояние по найденной линии, но с приращением (для большего размера до линии БД) или с убавлением (для меньшего размера до линии БГ). Полученное расстояние (1 –1 ''' и т. д.) откладывают от оси О'Х' (см. рис. VIII. 3, б) крайнего размера на соответствующей исходному размеру линии вверх или вниз.

Из рис. VIII. 3, а видно, что не все характерные точки лежат на основных делительных линиях. Чтобы установить их положение и других необходимых для построения точек на крайнем размере, расстояние до них на оси О'Х' определяют по формуле (7). После соответствующих преобразований получаем

Например, расстояние до точки б' на крайнем размере составит

а расстояние до точки г ' составит

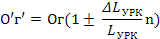
После получения грунтмодели крайнего размера градируют детали. Градирование можно выполнять графически, для чего детали исходного и крайнего размеров сдвигают на удобное для деления на п отрезков расстояние, как показано на рис. VIII. 2, ж. Соединив прямыми линиями все идентичные (характерные) точки, делят полученные между ними отрезки с помощью делительного треугольника или циркуля.

Глава 3

⇐ Предыдущая 98 99 100 101 102103104 105 106 107 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском:

vikidalka.ru - 2015-2024 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных