Тогда как при имеем

. (40₂)

Таким образом при соблюдении условия (36) и при подстройке системы так, чтобы

, если (41₁)

И

, если (41₂)

Мы можем периодическим изменением самоиндукции с частотой 2w возбудить в системе, настроенной приблизительно на частотуw, колебания частоты, стационарная амплитуда которых будет дана выражением (401) или (402).

Как видно из (41₁) и (41₂) теория в первом приближении ограничивает расстройку x только с одной стороны, т. е. возможны устойчивые значения амплитуды и за пределами интервала значений x, определяемого условием возникновения колебаний. Иными словами, параметрически возбужденные колебания "затягиваются". Как далеко простирается эта наблюдаемая и на опыте "область затягивания", из полученных приближенных выражений для амплитуды не вытекает. Для того чтобы получить ответ на этот и другие относящиеся сюда вопросы, нельзя ограничиться рассмотренным нами "нулевым" приближением, а необходимо учесть влияние членов, содержащих m на амплитуду основной гармоники, а также и роль обертонов. Следует заметить, что к аналогичным результатам приводит нулевое решение и для случая, когда зависимость между потоком и током в ограничивающем дросселе выражена?аркустангенcоидой? (¹⁹), который разобран в статье В. П. Гуляева и В. В. Мигулина.

Рассмотрим ближе характер зависимости амплитуды параметрически возбужденных колебаний от определяющих ее величин. На рис. 3 и 4 представлены кривые зависимости X ² от расстройки x, которые можно назвать кривыми гетеропараметрического резонанса. Легко видеть, что эти кривые существенным образом отличаются, как от обычных резонансных кривых, так и от кривых, резонанса 2-го рода. Как видно из рис. 3, пока

(при )

никаких заметных колебаний в системе нет.
При:

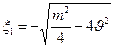
Параметрические колебания возникают, начинаясь с очень маленьких амплитуд и при дальнейшем увеличении x увеличиваются. X2 растет при этом прямолинейно до тех пор, пока при некотором значении

.

Колебания резко обрываются. При обратном ходе расстройки колебания возникают уже при и затем при дальнейшем уменьшении x уменьшаются до тех пор, пока при X 2 снова не сделается равным нулю.

Таким образом, только с одной стороны существует "петля затягивания" (рис.3)

Рис. 3. Кривая гетеропарамет­рического резонанса ().	Рис. 4. Кривая гетеропарамет­рического резонанса ().

Как видно из рис. 4, при мы имеем обратную картину: X ² растет с уменьшением x и петля затягивания имеется при x = x ₁. Максимальная величина Х ² внутри области возникновения колебаний равна:

Не нашли, что искали? Воспользуйтесь поиском: