Так как в этом случае после подстановки (24) в (202) получаем

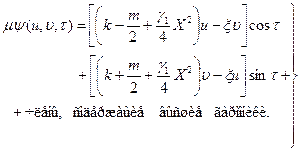(45)

то уравнения (27₁) и (27₂) для a и b принимают здесь следующий вид:

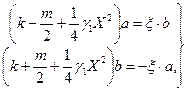(46)

откуда имеем либо:

,

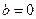
Либо

(47)

Или

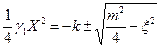. (47₁)

Для выяснения физических условий, необходимых для наличия того или иного из этих решений, обратимся к условиям устойчивости. Так как в данном случае:

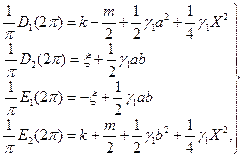(48)

то условия (28) и (29) принимают следующий вид: Для случая ,

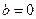
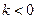(49₁)

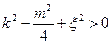(49₂)

Для случая ,

(50₁)

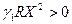. (50₂)

Здесь R означает. Из этих соотношений можно сделать следующие выводы.Преждевсего из (491) и (492) следует, что когда k < 0, т. е. когда система не самовозбуждена (сравни формул (30)), параметрическое возбуждение возможно лишь при

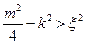. (51)

Сравнивая эту формулу с формулой (36) для нерегенерированной системы, мы видим, что вместо 2J мы здесь имеем меньшую величину. Таким образом, можно, применяя регенерацию возбудить параметрические колебания в системе и тогда, когда данная глубина модуляции параметра m недостаточна для выполнения условия (36). Этот вывод лег в основу некоторых из описываемых ниже опытов.

Если выполнено условие (61), то состояние системы при a = 0, b = 0 неустойчиво. В случае установившегося периодического движения оно передается формулой (47). Из условий (50₁) и (50₂) следует, что выражаемое ими состояние устойчиво, лишь если одновременно и R меньше 0. Таким образом мы приходим к заключению, что амплитуда стационарных периодических колебаний выражается формулой:

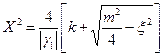. (47₂)

Эта формула верна как для k меньше 0, (несамовозбужденная система), так и для k > 0 (самовозбужденная система). Рассмотрим сначала первый случай. Прежде всего заметим, что условие реальности X совпадает с условием возбуждения параметрических колебаний (51). Отсюда следует, что, как и при автопараметрическом возбуждении, и здесь при "мягком" режиме возбуждения явление "затягивания" отсутствует. Если мы сравним далее формулу (47₂) с соответствующей формулой для амплитуды колебаний при автопараметрическом возбуждении: (18)

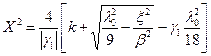, (52)

то увидим, что обе формулы вполне аналогичны и при малых l ₀ практически совпадают. Таким образом, кривые гетеропараметрического резонанса, в рассматриваемой случае вполне подобны рассмотренным нами раньше (¹⁷) и (¹⁸) кривым автопараметрического резонанса (резонанса 2-го рода), причем внешнюю силу здесь заменяет
вычисленная по формуле (47₂) кривая гетеропараметрического резонанса. Как видно из нее, кривая резонанса при ограничении амплитуды нелинейным сопротивлением существенно отличается от кривой гетеропараметрического резонанса при ограничении амплитуды с помощью нелинейной самоиндукции (сравни рис. 3 и 4).
В случае изменения параметра в самовозбужденной системе (k > 0) мы приходим к следующим заключениям. Прежде всего, из самого факта существования устойчивого периодического решения (47₁) следует, что и при гетеропараметрическом воздействии на автоколебательную систему имеет место явление принудительной синхронизации ("увлечение частоты"). Далее, так как реальность X обусловлена при k > 0 только реальностью корня, то мы имеем для "области увлечения" следующее соотношение:

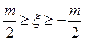, (53)

Не нашли, что искали? Воспользуйтесь поиском: