Законы Кирхгофа для мгновенных значений цепей изменяющегося тока 4 страница

Автотрансформаторное (неполное) включение контура – ДОДЕЛАТЬ111

сли соединить последовательно электрический конденсатор и катушку индуктивности, то для синусоидального сигнала определенной частоты указанная схема будет демонстрировать нулевое реактивное сопротивление. Этот эффект называется резонансом колебательного контура, сама схема из конденсатора и индуктивности - последовательным колебательным контуром, а частота, на которой проявляется этот эффект - частотой резонанса.

Хотя и катушка индуктивности, и конденсатор имеют некоторое реактивное сопротивление, вместе они реактивного сопротивления не проявляют. Причина проста. Конденсатор и катушка накапливают и отдают энергию, но делают это по-разному. В тот момент, когда катушка накапливает энергию, конденсатор ее отдает, и наоборот. Конечно, этот эффект проявляется только для синусоидального сигнала, на определенной частоте, в установившемся режиме. Если частота сильно отличается от резонансной, то схема теряет свои чудесные качества и проявляет себя, как катушка и конденсатор. Если последовательный колебательный контур не был запитан, а теперь на него подали синусоидальный сигнал резонансной частоты, то сопротивление будет уменьшаться постепенно, по мере перехода контура в стационарный режим работы.

Если пропускать через последовательный колебательный контур синусоидальный электрический ток резонансной частоты, то падение напряжения на контуре будет равно нулю. Но падение напряжения на конденсаторе отдельно, индуктивности отдельно будет иметь место. Просто эти напряжения компенсируют друг друга в каждый момент времени. Напряжения на конденсаторе и катушке могут быть очень значительными. Одной из популярных ошибок при проектировании последовательного колебательного контура является неправильная оценка напряжения на конденсаторе. Напряжение может в разы, десятки, сотни раз превышать напряжение источника питания. На основе этого эффекта даже разработаны схемы повышающих преобразователей напряжения.

[ Амплитудное значение напряжения на конденсаторе, В ] = [ Амплитудное значение силы тока через контур, А ] * [ ZC ], где [ ZC ] = 1 / (2 * ПИ * [ Частота сигнала, Гц ] * [ Емкость конденсатора, Ф ])

Необходимо также обратить внимание, чтобы ток через последовательный контур не приводил к насыщению сердечника катушки индуктивности.

В схемотехнике последовательный колебательный контур применяется, если необходимо пропустить сигнал определенной частоты и отфильтровать все другие. Колебательные контуры бывают небольшие, рассчитанные на работу с небольшими токами и напряжениями, например, во входных и внутренних цепях радиоприемника. Но бывают и силовые, рассчитанные на большие токи и напряжения, например, в радиопередатчиках, силовых резонансных фильтрах и т. д.

58. Связанные контуры используются в резонансных усилителях приемно-пере-дающих устройств. Наибольшее распространение получили двухконтурные системы, показанные на рис. 13.15 и 13.16. На них обозначено: Ui, Uo — напряжения на входе и выходе контуров; М — коэффициент взаимной индуктивности; Ro, Co, Lo — элементы связи; LI, Cl, Rl, L2, С2, R2 — элементы первого и второго контуров.

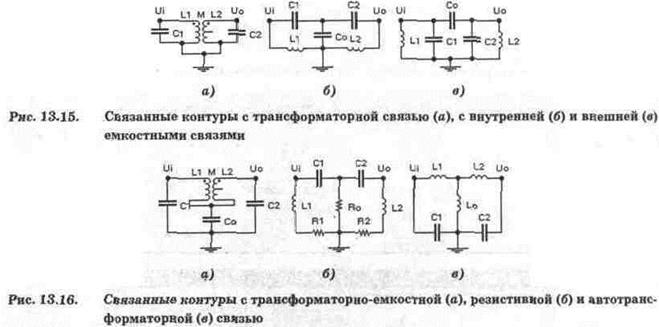
Одной из важнейших характеристик связанных контуров является коэффициент связи , где К1 К2 — коэффициенты связи для первого и второго контуров. Коэффициент связи служит для количественной оценки взаимного влияния контуров и в практических конструкциях обычно существенно меньше единицы.

Для схемы на рис. 13.15, а

Для схемы на рис. 13.15, б

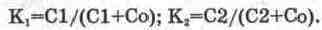
Для схемы на рис. 13.15, е

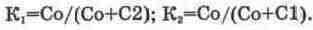
Для схемы на рис. 13.16, а

Для схемы на рис. 13.16, б

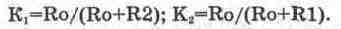
Для схемы на рис. 13.16, в

В качестве объекта исследования выберем схему на рис. 13.15, в, которая с дополнительными элементами показана на рис. 13.17. Она дополнена резисторами R1 и R2, имитирующими активные сопротивления катушек индуктивности. Переключатель Z позволяет реализовать два режима: измерение АЧХ и ФЧХ (в положении переключателя, показанном на рисунке) и исследование прохождения AM сигналов через систему связанных контуров.

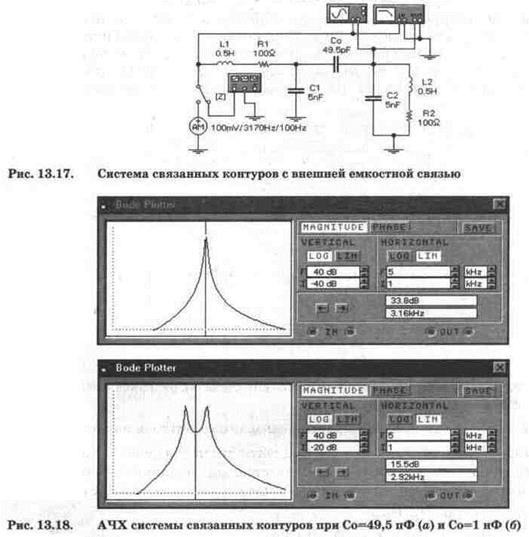
Параметры системы связанных контуров определятся коэффициентом связи, затуханием одиночного контура D (величина, обратная добротности) и резонансными частотами каждого контура. Поскольку для схемы на рис. 13.17 С1=С2=С, L1=L2=L, R1=R2=R, то эти параметры определяются с помощью выражений [58]:

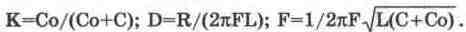
Для связанных контуров характерным является наличие двух частот связи [58]

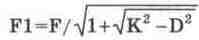и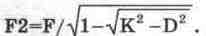

Для схемы на рис. 13.17 расчеты по этим формулам при K=D=0,01 (режим критической связи) дают: F1=F2=F=3,17 кГц, т.е. частоты связи практически совпадают, а АЧХ (рис. 13.18, а) представляет собой одногорбую резонансную кривую.

Увеличим коэффициент связи, выбрав Со=1 нФ. Для этого случая параметры схемы имеют следующие расчетные значения: К=0,176; F=2,9 кГц; F1=2,7 кГц;

F2=3,18 кГц. Результаты моделирования приведены на рис. 13.18, б, откуда видно, что АЧХ при коэффициенте связи выше критического имеет двугорбый характер, соответствующий двум частотам связи, и отличается более крутыми скатами АЧХ при более широкой полосе пропускания, которая обычно определяется на уровне 0,707 (-3 дБ) и равна AF=F-D (F — резонансная частота). Анализ показывает [51, 58], что полоса пропускания связанных контуров при критической связи (K=D) составляет 1.41F-D и достигает максимального значения 3.1F-D при K=2,41D. Следует отметить, что при связи контуров ниже критической (K<D) полоса пропускания двухконтурной системы может быть меньше полосы пропускания одиночного контура. Так, например, при K=0,1D полоса пропускания составляет 0,65F-D. Это свойство связанных контуров часто используется на практике, когда требуется получить полосу пропускания уже полосы пропускания одиночного контура.

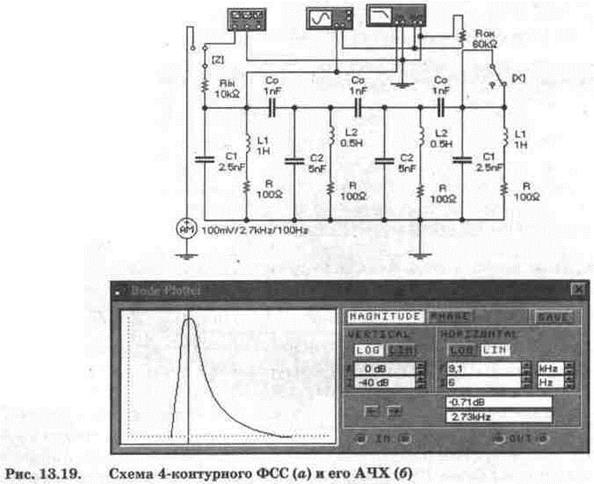
В заключение рассмотрим многоконтурную систему связанных контуров, используемую в качестве фильтра сосредоточенной селекции (ФСС) в каскаде преобразователя частоты многих радиоприемников. Анализ показывает [59], что наиболее эффективной (по критерию качество-стоимость) является 4-контурная система (рис. 13.19, а), представляющая собой набор из контуров двух типов: два крайних имеют увеличенную в два раза индуктивность и уменьшенную в два раза емкость по сравнению со средними двумя контурами, т.е. все четыре контура имеет одинаковую собственную резонансную частоту. Увеличение индуктивности двух крайних контуров

позволяет увеличить характеристическое сопротивление этих контуров

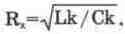
Такой выбор позволяет выравнять коэффициенты передачи всех контуров при включении на входе и выходе фильтра согласующих сопротивлений Rim и Rox, шунтирующих Rx крайних контуров. Однако такое конструктивное выполнение контуров, как будет показано ниже на практическом примере, не является обязательным. Заметим, что наибольшее влияние на форму АЧХ оказывает сопротивление Rox, поэтому в схеме использован переключатель Х для возможности оперативного исследования влияния этого сопротивления. Емкость конденсаторов связи Со выбирается, в зависимости от требуемой полосы пропускания, из необходимого соотношения коэффициента связи К и затухания D. Указанное на рис. 13.19, а значение емкостей Со, обеспечивающих связь выше критической, выбрано из соображения наглядности, чтобы показать основное преимущество рассматриваемого фильтра, заключающееся в обеспечении широкой полосы пропускания при достаточно крутых скатах резонансной кривой.

АЧХ фильтра при указанных на рис. 13.19, а параметрах показана на рис. 13.19, б. Из сравнения этой АЧХ с ранее полученными для двухконтурных систем (см. рис. 13.18) видно, что 4-контурная система имеет явно выраженную плоскую часть АЧХ. Однако такая гладкая вершина АЧХ достигается только при соответствующем выборе сопротивления согласующего резистора.

Следует отметить, что расчет многозвенных фильтров является достаточно сложной задачей. В работе [59] приводятся следующие соотношения для расчета параметров рассматриваемого фильтра:

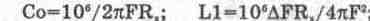
— требуемая полоса; емкость — в пФ;

индуктивность — в мкГ; частота — в кГц; сопротивление — в кОм.

Два контура называются связанными, если колебания, происходя­щие в одном из них, захватывают другой контур. Связь между кон­турами может осуществляться через электрическое поле (благодаря емкости) или через магнитное поле (благодаря взаимоиндуктивности или индуктивности). На рис. 1 показаны три разновидности связи двух колебательных контуров: а) трансформаторная, когда связь между контурами осуществляется благодаря взаимоиндуктивности между катушками L1 и L2; б) автотрансформаторная, когда связь между контурами осуществляется непосредственно через индуктивность связи L1,2; в) емкостная, когда связь между контурами осуществляется через емкость связи С3. Наиболее часто в радиотехнике применяется трансформаторная связь, поэтому все дальнейшие выкладки проведем для этого вида связи.

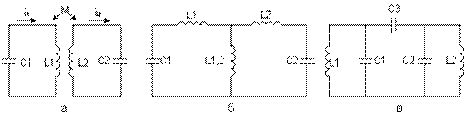
Рис. 1. Виды связи двух колебательных контуров

Предположим, что в первом контуре на рис.1, а протекает ток i1, а второй контур разомкнут. Тогда отношение напряжения, индуцированного в катушке L2, к напряжению в катушке L1 выразится коэффициентом

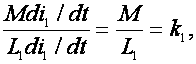
который называется степенью связи. Аналогично, если предположить разомкнутым первый контур, а источник э.д.с. подключить ко второму контуру, то при протекании в нем тока i2 получим

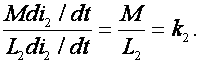
Коэффициент связи есть корень квадратный из произведения степеней связи . (1)

При трансформаторной связи 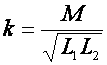. (2)

Если умножить числитель и знаменатель (2) на w, то получим общее выражение для коэффициента связи, пригодное и для других видов связи

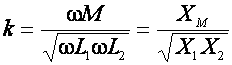(3)

где XM - сопротивление связи.

Не нашли, что искали? Воспользуйтесь поиском: