УРАВНЕНИЕ ДИНАМИКИ ВРАЩЕНИЯ ТВЕРДОГО ТЕЛА

Момент инерции. Твердое тело можно представить в виде системы жестко связанных между собой материальных точек.
Момент инерции системы материальных точек относительно оси вращения равен сумме произведений масс материальных точек системы на квадраты их расстояний до оси вращения:
.

Для расчета момента инерции используют интегрирование:
.

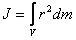Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиуса	Ось симметрии
Сплошной цилиндр или диск радиуса	Ось симметрии
Прямой тонкий стержень длиной	Ось перпендикулярна стержню и проходит через его середину.
Прямой тонкий стержень длиной	Ось перпендикулярна стержню и проходит через его конец
Шар радиусом	Ось проходит через центр шара

Теорема Штейнера. Момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями: .

Момент силы. Момент силы относительно точки .
Момент силы относительно неподвижной оси равен проекции вектора на эту ось.
Проекция вектора на ось не зависит от положения точки, относительно которой определяется радиус-вектор силы .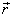
Если вектор лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.

Определение моментов сил: , .

Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси:
суммарный момент сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение:
.
Учитывая, что момент импульса твердого тела , уравнение динамики твердого тела можно представить в виде
.

9. Момент импульса. Закон сохранения момента импульса.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

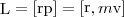
где r - радиус-вектор, проведенный из точки О в точку A, p =m v - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Рис.1

Модуль вектора момента импульса

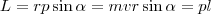
где α - угол между векторами r и р, l - плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_i со скоростью v_i. Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i. Значит, мы можем записать, что момент импульса отдельной частицы равен

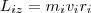(1)

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

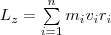
Используя формулу v_i = ωr_i, получим

т. е. 2)

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство

(3)

В замкнутой системе момент внешних сил 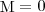и откуда

(4)

Выражение является законом сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).

Не нашли, что искали? Воспользуйтесь поиском: