Свободные незатухающие колебания. Свободные колебания могут быть незатухающими только при отсутствии силы трения

Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться.

В качестве примера рассмотрим колебания тела, подвешенного на невесомой пружине, возникающие после того, как тело отклонили вниз, а затем отпустили (рис. 1.2).

Рис. 1.2. Колебания тела на пружине

Со стороны растянутой пружины на тело действует упругая сила F, пропорциональная величине смещения х:

Постоянный множитель k называется жесткостью пружины и зависит от ее размеров и материала. Знак «-» указывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т.е. к положению равновесия.

При отсутствии трения упругая сила (1.4) - это единственная сила, действующая на тело. Согласно второму закону Ньютона (ma = F):

После переноса всех слагаемых в левую часть и деления на массу тела (m) получим дифференциальное уравнение свободных колебаний при отсутствии трения:

Величина ω₀ (1.6) оказалась равной циклической частоте. Эту частоту называют собственной.

Таким образом, свободные колебания при отсутствии трения являются гармоническими, если при отклонении от положения равновесия возникает упругая сила (1.4).

Собственная круговая частота является основной характеристикой свободных гармонических колебаний. Эта величина зависит только от свойств колебательной системы (в рассматриваемом случае - от массы тела и жесткости пружины). В дальнейшем символ ω₀ всегда будет использоваться для обозначения собственной круговой частоты (т.е. частоты, с которой происходили бы колебания при отсутствии силы трения).

Амплитуда свободных колебаний определяется свойствами колебательной системы (m, k) и энергией, сообщенной ей в начальный момент времени.

При отсутствии трения свободные колебания, близкие к гармоническим, возникают также и в других системах: математический и физический маятники (теория этих вопросов не рассматривается) (рис. 1.3).

Математический маятник - небольшое тело (материальная точка), подвешенное на невесомой нити (рис. 1.3 а). Если нить отклонить от положения равновесия на небольшой (до 5°) угол α и отпустить, то тело будет совершать колебания с периодом, определяемым по формуле

где L - длина нити, g - ускорение свободного падения.

Рис. 1.3. Математический маятник (а), физический маятник (б)

Физический маятник - твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси. На рисунке 1.3 б схематически изображен физический маятник в виде тела произвольной формы, отклоненного от положения равновесия на угол α. Период колебаний физического маятника описывается формулой

где J - момент инерции тела относительно оси, m - масса, h - расстояние между центром тяжести (точка С) и осью подвеса (точка О).

Момент инерции - это величина, зависящая от массы тела, его размеров и положения относительно оси вращения. Вычисляется момент инерции по специальным формулам.

1.. Гармонические колебания и их характеристики.

Колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени, т.е. колебания - периодические изменения какой-либо величины.

В зависимости от физической природы различают механические и электромагнитные колебания. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.

Колебания называются периодическими, если значения всех физических величин, изменяющихся при колебаниях системы, повторяются через равные промежутки времени.

Период - это время, за которое совершается одно полное колебание:

,

где - число колебаний за время .

Частота колебаний - число полных колебаний, совершенных за единицу времени.

(единиц времени):pЦиклическая или круговая частота - число полных колебаний, совершенных за время 2

.

Простейшим типом колебаний являются гармонические колебания, при которых изменение величины происходит по закону синуса или косинуса (рис.1):

,

где - значение изменяющейся величины;

- амплитуда колебаний, максимальное значение изменяющейся величины;

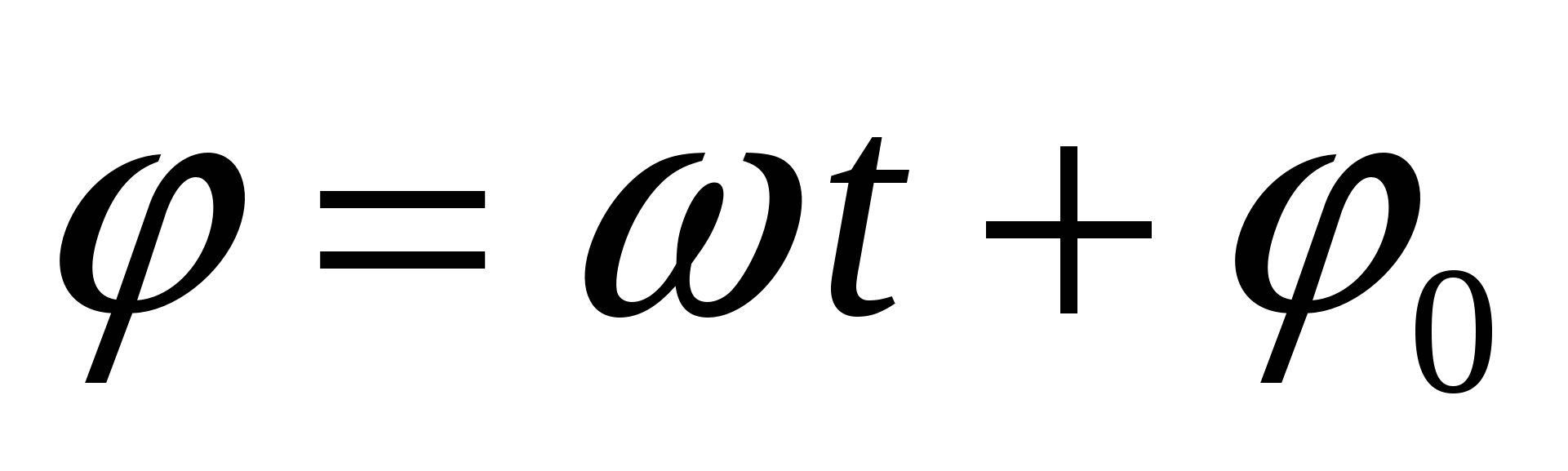- фаза колебаний в момент времени (угловая мера времени);

j₀- начальная фаза, определяет значение в начальный момент времени при , .

Колебательная система, совершающая гармонические колебания, называется гармоническим осциллятором.

Скорость и ускорение при гармонических колебаниях:

:.

Не нашли, что искали? Воспользуйтесь поиском: