
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лекции №5, 6. Дистилляция. Ректификация.
Однократная простая дистилляция. Схема. Принцип действия.
Схема установки однократной простой дистилляции представлена на рисунке 1.

|
| Dп, iK |
| Dп, h |
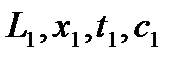
|
| 1 |
| Gв, tв’’ |
| 2 |
| 3 |
| ’ |
| Gв, tв’ |

|

|
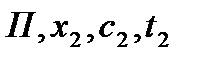
|
| К1 |
| К2 |
| К3 |
Рис. 1. Схема однократной простой дистилляции: 1 – куб – кипятильник; 2 – конденсатор; 3 – сборник продукта.
В куб – кипятильник непрерывно подается исходная бинарная смесь в количестве L1 состава x1. В трубное пространство кипятильника непрерывно подается греющий пар в количестве Dгр давления рп. В результате процесса тепло и массообмена: в кубе кипит смесь состава x0; из куба отводится паровая смесь в количестве D состава y2 и кубовый остаток в количестве L0 состава x0. Паровая смесь направляется в конденсатор установки, где происходит его полная конденсация. Образовавшийся таким образом продукт, в количестве П состава x2, направляется в сборник продукта. Поток образовавшегося продукта равен потоку пара, а состав продукта равен составу пара.
Предельные температуры ведения процесса дистилляции при известном давлении в кубе в предположении, что пар, покидающий куб, находится в равновесии с кубовой жидкостью.
Процесс дистилляции реализуется только при наличии двух фаз: паровой и жидкой.
Условия проведения процесса дистилляции, при которых сохраняется число, и вид фаз системы формулируется правилом фаз
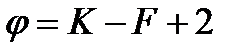 , где
, где  – число степеней свободы, К – число компонентов системы, F – число фаз системы.
– число степеней свободы, К – число компонентов системы, F – число фаз системы.
Число степеней свободы показывает число параметров ( ,y), которые можно произвольно менять (в определенных пределах) не изменяя числа и вида фаз системы. Для дистилляции:
,y), которые можно произвольно менять (в определенных пределах) не изменяя числа и вида фаз системы. Для дистилляции:  = 2 – 2 – 2 = 2. Выбирая диаграмму фазового равновесия для анализа процесса в координатах
= 2 – 2 – 2 = 2. Выбирая диаграмму фазового равновесия для анализа процесса в координатах  , назначают величину первого из двух параметров, которые можно менять – давление; таким образом, остается второй параметр, который можно произвольно изменять, это или температура или состав одной из фаз находящихся в равновесии, тогда значение третьего и четвертого параметров будут определяться однозначно первыми двумя. В рассматриваемом случае выбор пал на температуру процесса, пределы варьирования которой должны быть определены. Назначив температуру процесса в допустимых пределах, однозначно определяем равновесные составы пара и жидкости.
, назначают величину первого из двух параметров, которые можно менять – давление; таким образом, остается второй параметр, который можно произвольно изменять, это или температура или состав одной из фаз находящихся в равновесии, тогда значение третьего и четвертого параметров будут определяться однозначно первыми двумя. В рассматриваемом случае выбор пал на температуру процесса, пределы варьирования которой должны быть определены. Назначив температуру процесса в допустимых пределах, однозначно определяем равновесные составы пара и жидкости.
Для определения предельных температур процесса достаточно провести вертикаль x1 в диаграмме «температура – состав» (см. рис. 2.) до пересечения с линиями пара и жидкости. Ординаты точек пересечения указывают на предельные температуры ведения процесса.
| t |
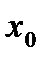
|

|
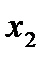
|
| tmax |
| c |
| b |
| a |
| t |
| tmin |
Рис.2. Диаграмма t – x,y.
Уравнения материального баланса. Определение потоков продукта и кубового остатка. Правило рычага 2 го рода.
Составим уравнения материального баланса для установки однократной простой дистилляции по смеси и по низкокипящему компоненту (см. рисунок установки, контур К1).
По смеси
 . (1)
. (1)
По НКК
 . (2)
. (2)
Решая совместно уравнения (1) и (2) относительно продукта и кубового остатка, получим
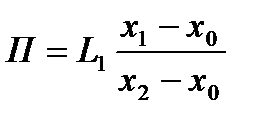 . (3)
. (3)
 . (4)
. (4)
Поделив и числитель, и знаменатель дробного сомножителя правой части каждого из последних двух уравнений на масштаб по оси x, получим уравнения в виде (см. рис. 2.)
 (5)
(5)
 (6)
(6)
Уравнения (5) и (6) традиционно толкуются как правила рычага второго рода (см. рис. 2.). Здесь т. a соответствует составу кубового остатка, т. b – составу исходной смеси, т. c – составу продукта.
Анализ влияния температуры процесса на составы и потоки продукта и кубового остатка.
Анализ уравнения (5) и диаграммы «t – x,y» показывает, что с уменьшением температуры ведения процесса дистилляции увеличивается состав продукта по А, но уменьшается его расход. В пределе, если температура процесса достигает значения минимально возможного, получают максимальное содержание НКК в продукте при нулевом количестве продукта.
Анализ влияния (6) и диаграммы «t – x,y» показывает, что с увеличением температуры ведения процесса дистилляции увеличивается состав кубового остатка по В, но уменьшается его расход. В пределе, если температура процесса достигает значения максимально возможного, получают максимальное содержание ВКК в кубовом остатке при нулевом расходе его.
Уравнения теплового баланса куба. Мощность кипятильника куба. Расход греющего пара. Мощность конденсатора. Расход охлаждающей воды в конденсаторе.
Составим уравнение теплового баланса для куба дистилляционной установки (см. рис.1. контур К2):
 , откуда следует, что мощность кипятильника может быть рассчитана по формуле
, откуда следует, что мощность кипятильника может быть рассчитана по формуле
 , (7.)
, (7.)
где i2 – энтальпия пара состава y2.
Уравнение справедливо при условии идеальной теплоизоляции куба.
Расход греющего пара
 , (8)
, (8)
где h – энтальпия греющего пара, iK - энтальпия конденсата греющего пара.
Составим уравнение теплового баланса для конденсатора дистилляционной установки (см. рис.1. контур К3):
 , откуда следует, что мощность конденсатора
, откуда следует, что мощность конденсатора
 . (9)
. (9)
Расход охлаждающей воды в конденсаторе
 . (10)
. (10)
Примечание. Однократная простая дистилляция не позволяет получить практически чистые компоненты смеси в качестве продукта и кубового остатка.
Ректификационная колонна непрерывного действия, тарельчатая. Схема ректификационной установки. Отгонная часть колонны. Укрепляющая часть колонны. Тарелка питания.
Схема ректификационной колонны непрерывного действия представлена на рисунке 3.
Часть колонны, расположенная ниже тарелки питания, включая эту тарелку, носит название отгонной части колонны. Происхождение названия: в этой части из потока жидкости отгоняется НКК.
Часть колонны, расположенная выше тарелки питания, называется укрепляющей частью колонны. Происхождение названия: в этой части колонны паровой поток укрепляется НКК.
Тарелкой питания называют тарелку, на которую подается исходная смесь. Тарелка питания принадлежит отгонной части колонны, так как эта тарелка, как и все тарелки нижней части колонны, орошается жидкостным потоком равным сумме потоков флегмы и исходной смеси.
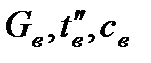
|

|

|

|

|

|
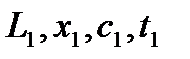
|

|

|

|

|
| К1 |
| К2 |
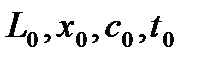
|
Рис. 3. Схема ректификационной установки непрерывного действия.
Ректификационная колонна в нижней части снабжена кипятильником, назначение которого заключается в генерации парового потока по колонне. В межтрубное пространство кипятильника подается греющий пар, обеспечивающий кипение кубовой жидкости в трубном пространстве кипятильника.
В верхней части колонна снабжена конденсатором, в котором происходит полная конденсация поступающей в межтрубное пространство паровой смеси. Поток конденсата, выходящий из конденсатора, делится на две части. Первая часть, называемая флегмой, возвращается в колонну, обеспечивая поток жидкости по колонне, следуемый навстречу потоку пара. Вторая часть конденсата называется продуктом. На каждой из тарелок происходит процесс тепломассообмена (конденсация части пара и испарение части жидкости, т.к. температура пара несколько выше температуры пара), в результате которого пар обогащается НКК, а жидкость, напротив, обогащается ВКК. Таким образом, паровой поток на выходе из колонны максимально обогащен НКК, а жидкостной поток на выходе из колонны максимально обогащен ВКК. Т.е. продукт при достаточном количестве тарелок будет практически чистым НКК, а кубовый остаток – практически чистым ВКК.
Определение потоков продукта и кубового остатка.
Составим уравнение материального баланса по смеси для всей колонны (см. рис.4).
 .
.
Составим уравнение материального баланса по НКК для всей колонны
 .
.
Совместное решение этих двух уравнение дает расчетные выражения для определения потоков продукта и кубового остатка
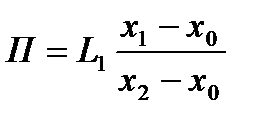 ,
,  ; или
; или  ,
, 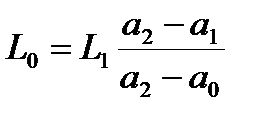 .
.

|

|

|
Рис.4. К определению потоков продукта и кубового остатка.
Задача проектирования. Число действительных тарелок (ступеней). Число теоретических тарелок.
Коэффициент полезного действия тарелки. Рабочая линия процесса. Сопряженные концентрации.
При решении задач проектирования определяют геометрические размеры колонны – ее высоту и диаметр. Высота колонны определяется в основном числом действительных тарелок. В свою очередь число действительных тарелок зависит от числа теоретических тарелок и коэффициента полезного действия действительной тарелки ( ,
,  конструкции тарелки). Для определения числа теоретических тарелок, как меры эффективности работы ректификационной колонны, необходимо знать расположение двух замечательных линий в диаграмме фазового равновесия – линии равновесия и рабочей линии. Рабочей линией называется геометрическое место точек сопряженных концентраций потоков жидкости и пара в колонне. Сопряженными концентрациями называют составы потоков в любом поперечном сечении колонны. Так например, согласно рисунку 5. первая пара сопряженных концентраций это” xi, yi “, вторая пара сопряженных концентраций – “ ” xi+1, yi+1 “.
конструкции тарелки). Для определения числа теоретических тарелок, как меры эффективности работы ректификационной колонны, необходимо знать расположение двух замечательных линий в диаграмме фазового равновесия – линии равновесия и рабочей линии. Рабочей линией называется геометрическое место точек сопряженных концентраций потоков жидкости и пара в колонне. Сопряженными концентрациями называют составы потоков в любом поперечном сечении колонны. Так например, согласно рисунку 5. первая пара сопряженных концентраций это” xi, yi “, вторая пара сопряженных концентраций – “ ” xi+1, yi+1 “.
yi+1 xi+1
yi xi
Рис.5. Сопряженные концентрации. Равновесные концентрации. Теоретическая ступень.
Иными словами рабочая линия показывает: как меняются составы потоков пара жидкости по высоте колонны.
Уравнение рабочей линии укрепляющей части ректификационной колонны.
Для вывода уравнения рабочей линии верхней части колонны составим уравнение материального баланса по НКК для контура 1 с произвольным сечением верхней части колонны (рис.3.)
 , откуда
, откуда  . (11)
. (11)
Уравнение (11) – уравнение рабочей линии укрепляющей части колонны. Преобразуем уравнение (11), введя понятие флегмового числа:  . Флегмовое число показывает, какое количество конденсата после конденсатора возвращается в колонны в качестве флегмы на единицу продукта.
. Флегмовое число показывает, какое количество конденсата после конденсатора возвращается в колонны в качестве флегмы на единицу продукта.
Поделив числитель и знаменатель каждого из слагаемых уравнения (1) на П, получим
 . Но согласно уравнению материального баланса узла разделения (контур 2, рис.3.) по смеси имеем
. Но согласно уравнению материального баланса узла разделения (контур 2, рис.3.) по смеси имеем
 .
.
В результате комбинации последних двух уравнений получим уравнение рабочей линии в традиционном виде
 . (12)
. (12)
Предполагая равенство скрытых теплот конденсации - испарения ( компонентов разделяемой смеси, можно с определенной долей погрешности утверждать, что уравнение (12) является уравнением прямой линии в координатах “y – x” (на каждой ступени при конденсации одного кмоля пара образуется кмоль пара по составу превосходящий первый, следовательно потоки пара и жидкости по высоте укрепляющей части колонны остаются постоянными).
компонентов разделяемой смеси, можно с определенной долей погрешности утверждать, что уравнение (12) является уравнением прямой линии в координатах “y – x” (на каждой ступени при конденсации одного кмоля пара образуется кмоль пара по составу превосходящий первый, следовательно потоки пара и жидкости по высоте укрепляющей части колонны остаются постоянными).
Определение координат точек пересечения рабочей линии с диагональю и осью ординат диаграммы фазового равновесия «y – x”. Графическая интерпретация уравнения в координатах «y – x”.
Для определения положения рабочей линии необходимо знать координаты точек пересечения её с диагональю и с осью ординат. Начнем с первой точки. Запишем уравнение диагонали
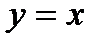

|
| y |
| x |
| x2 |
| x0 |
| x1 |
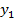
|
| y2 |
 y2 y2
|
(
|

|
 , следовательно, координаты первой искомой точки найдены, это (
, следовательно, координаты первой искомой точки найдены, это ( ) (см. рис.6.)
) (см. рис.6.)
Рис.6. Диаграмма «y – x». Графическая интерпретация уравнения рабочей линии укрепляющей части колонны. Построение теоретических тарелок (ступеней). Определение числа т.т.
Для определения координат точки пересечения рабочей линии с осью ординат напишем уравнение оси ординат, это x = 0. Решая совместно уравнение (12) с уравнением оси ординат, получим ординату точки пересечения этих двух линий  , следовательно, координаты второй искомой точки найдены, это (0, b).
, следовательно, координаты второй искомой точки найдены, это (0, b).
Соединив найденные точки прямой линией, выделим на этой линии собственно рабочую линию укрепляющей части колонны на участке от x1 до x2. Строим теоретические тарелки. Определяем их число. Под теоретической тарелкой понимают такое гипотетическое устройство, на выходе из которого взаимодействующие фазы находятся в равновесном состоянии (по рисунку 5. равновесными концентрациями являются  и
и  Геометрическим образом теоретической тарелки является прямоугольный треугольник, гипотенуза которого опирается на рабочую линию процесса, а вершина прямого угла треугольника лежит на линии равновесия. Построение теоретических ступеней начинают от точки (
Геометрическим образом теоретической тарелки является прямоугольный треугольник, гипотенуза которого опирается на рабочую линию процесса, а вершина прямого угла треугольника лежит на линии равновесия. Построение теоретических ступеней начинают от точки ( ) и завершают в точке (
) и завершают в точке ( ).
).
Предельные положения рабочей линии. Расход флегмы при предельных положениях рабочей линии. Число теоретических тарелок при предельных положениях рабочей линии.
Рабочая линия укрепляющей части колонны имеет два предельных положения. Первому предельному положению соответствует минимальный расход флегмы и бесконечное число теоретических тарелок. Рабочая линия в этом случае пересекает линию равновесия в точке с координатами ( ) (см. рис.7.).
) (см. рис.7.).
Второму предельному положению рабочей линии соответствует безотборный режим работы колонны. Т.е., при таком режиме отсутствует потоки; продукта, исходной смеси и кубового остатка. Весь конденсат возвращается в колонну в качестве флегмы. Флегмовое число стремится к бесконечности. Число теоретических тарелок минимально. Такой режим работы колонны используется в лабораторных исследованиях и при пусковых работах промышленных колонн. Уравнение рабочей линии укрепляющей части колонны трансформируется в уравнение диагонали. Поэтому, при безотборном режиме, рабочая линия совпадает с диагональю диаграммы 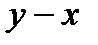 (см. рис.7.).
(см. рис.7.).
Вывод расчетного выражения для определения минимального флегмового числа.
| x2 |
| x1 |
| c |
| y1 |
| y2 |
| a |
| b |
Рабочая линия при 
|
Рабочая линия при 
|
 с соответствующими построениями.
с соответствующими построениями.
Рис.7. К выводу расчетного выражения минимального флегмового числа. Интерпретация рабочих линий при предельных значениях флегмового числа.
Из треугольника  следует, что тангенс угла наклона рабочей линии с минимальным флегмовым числом равен
следует, что тангенс угла наклона рабочей линии с минимальным флегмовым числом равен
 .
.
С другой стороны, согласно уравнению рабочей линии процесса
 ,
,
тангенс угла наклона рабочей линии равен
 .
.
Приравнивая правые части выражений для тангенса угла наклона, получим
 .
.
Число действительных ступеней (тарелок) при действительном флегмовом числе. Выражение для коэффициент избытка флегмы. Действительное флегмовое число.
Зная коэффициент избытка флегмы  , определяют действительное флегмовое число
, определяют действительное флегмовое число
 .
.
По найденному значению действительного флегмового числа определяют положение рабочей линии укрепляющей части колонны в координатах  по ранее описанному алгоритму. Далее определяют число теоретических тарелок. Зная коэффициент полезного действия действительной тарелки, определяют число действительных тарелок укрепляющей части колонны
по ранее описанному алгоритму. Далее определяют число теоретических тарелок. Зная коэффициент полезного действия действительной тарелки, определяют число действительных тарелок укрепляющей части колонны  .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Организация работ с поездами, длина которых превышает полезную длину приемо-отправочных путей станции. | | | ФОРМИРОВАНИЕ ЗАТРАТ И СЕБЕСТОИМОСТИ ПРОДУКЦИИ |
Не нашли, что искали? Воспользуйтесь поиском: