Сырғанау үйкелісі. Сырғанау үйкелісінің заңдары. Тегіс емес беттің реакциясы. Үйкеліс бұрышы.

Сырғанау үйкелісінің Кулон – Амонтон заңдары:

1. Бір денені басқа дене үстінде ығыстыруға тырысқан жағдайда олардың жанасу жазықтығында үйкеліс күші пайда болады, оның модулі 0 ≤ F≤ F_max аралығында кез келген мәнге ие болуы мүмкін. Үйкеліс күші денеге түседі және күш түскен нүктенің мүмкін жылдамдығына қарама-қарсы болады.

2. Максималды үйкеліс күші f үйкеліс коэффициенті мен N нормаль қысым күшінің көбейтіндісіне тең

F_max=f∙N. (3.10)

Үйкеліс коэффициенті жанасатын денелердің материалдары мен беттерінің қалпына (кедір-бұдырлығына, температурасына, ылғалдылығына және т.б.) тәуелді өлшем бірліксіз шама, ол тәжірибе арқылы анықталады. f мәндері: ағаш пен ағаш арасында 0,4-0,7; металл мен металл - 0,15-0,25; болат пен мұз - 0,027.

Тыныштық үйкелісі мен сырғанау үйкелісі айыра танылады. Тыныштық үйкелісінің коэффициенті тепе-теңдіктің шеткі қалпына, яғни сыртқы күштер кішкене ғана өскенде қозғалыс басталып кететін қалпына сәйкес келетін максималды F_max үйкеліс күші арқылы анықталады. Әдетте ол сырғанау үйкелісінің коэффициентінен артық. Сырғанау жылдамдығының өсуімен сырғанау үйкелісінің коэффициенті басында шамалы азаяды, содан кейін айтарлықтай өзгермейді.

3. Максималды үйкеліс күші едәуір кең шектерде жанасатын беттердің ауданына тәуелсіз.

Тегіс емес беттің реакциясы екі құраушы күштер арқылы есепке алынады: нормаль реакциясы (оның модулі нормаль қысым күшіне тең) және оған перпендикуляр үйкеліс күші (3.3 сурет). Толық реакция нормаль бағыттан α бұрышына ауытқиды (tg α = F/N).

Егер дене горизонталь тегіс емес беттің үстінде болып, оған ауырлық күштен басқа ешқандай сыртқы күш түспесе, онда F = 0, ал толық реакция R = N және тіреуіш бетіне перпендикуляр болады. Денеге шамасы аз күшін түсіріп, біз оны қозғалтуға тырыссақ, қозғалыс бола қалмайды, өйткені 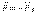үйкеліс күші пайда болады, және F≤ F_max. күші артқан сайын үйкеліс күші де артады. F₁ = F_max болғанда тепе-теңдіктің шеткі қалпы орын алады, сонда толық реакция вертикальдан үйкеліс бұрышы деп аталатын α_max бұрышына ауытқиды. Оны φ арқылы белгілеп, үйкеліс бұрышының тангенсі үйкеліс коэффициентіне тең екенін анықтаймыз

tg φ= F_max/N=f. (3.11)

Идеалды емес байланыстың толық реакциясының бағыты үйкеліс бұрышымен шеттеледі. Әдетте денелердің сырғанау үйкеліс күші ескерілуімен тепе-теңдіктің шеткі қалпы үшін үйкеліс күші максималды шамасына ие болғанда қарастырылады. Идеалды емес байланыстың реакциясы екі құраушымен көрсетіледі: N нормаль реакциясымен және F_max максималды үйкеліс күшімен.

Атты дененің ауырлық центрі. Дененің ауырлық центрінің координаттары. Ауырлық центрінің орнын анықтау тәсілдері: симметриялық пайдалану, қарапайым бөліктерге жіктеу, теріс массалар тәсілі.

Дененің А₁, A₂ нүктелерінде түсетін екі параллель және күштерін қарастырайық (3.5 сурет). тең әсерлі күшінің әсер ету сызығы қосылатын күштерге параллель және A₁A₂ түзуінде жатқан С нүктесінен өтеді. С нүктесінің орнын Вариньон теоремасын қолданып анықтай аламыз: , осыдан

. (3.13)

, күштерін А₁, А₂ нүктелерінің айналасында бірдей α бұрышына бұрғанда, тең әсерлі күші де сол бағытта α бұрышына бұрылады және дәл сол С нүктесіне түседі. С нүктесі параллель күштердің центрі деп аталады. Кез келген күштер саны үшін де осылай болады.

Дене бөлшектеріне түсет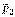ін , ,…, ауырлық күштерінің тең әсерлісін деп белгілейік (3.6 сурет). Осы күштің модулі дененің салмағы деп аталады және келесі теңдікпен анықталады

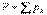. (3.14)

С нүктесі параллель ауырлық күштерінің центрі болып келеді, ол дененің ауырлық центрі деп аталады. Сонымен, АҚД-нің ауырлық центрі – денемен өзгеріссіз байланысқан дененің кеңістікте кез келген орналасуында дене бөлшектеріне түсетін ауырлық күштерінің тең әсерлі күшінің әсер ету сызығы өтетін нүкте. Ауырлық центрінің координаттары келесі формулалармен анықталады

, , (3.15)

мұндағы , , – ауырлық күштері түсетін нүктелердің координаттары.

Нүкте қозғалысының берілу тәсілдерінүкте қозғалысы векторлық тәсілмен берілген жағдайда нүктенің жылдамдығы мен үдеуі.

Нүктенің қозғалысы үш тәсілдердің біреуімен берілуі мүмкін.

1. Векторлық тәсіл. М нүктесі Oxyz санақ жүйесіне қатысты қозғалатын болсын. Нүктенің кез келген уақыт мезетіндегі орнын, оның 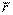радиус-векторының (4.1 сурет) t уақытына тәуелдігін беріп, анықтауға болады.

. (4.1)

Бұл векторлық түрде жазылған нүктенің қозғалыс заңы.

2. Координаттық тәсіл. Нүктенің орнын оның уақыт өтуімен өзгеретін координаттарымен тікелей анықтауға болады

. (4.2)

Бұл - тік бұрышты декарт координаттарындағы нүктенің қозғалыс заңы.

3. Табиғи тәсіл. Нүкте қозғалысын табиғи тәсілмен беру – бұл оның траекториясын (4.2 сурет), траекториясындағы санақ басы мен санақ бағытын және қозғалыс заңын келесі түрде беру

. (4.3)

Нүкте қозғалысының негізгі кинематикалық сипаттамаларының біреуі жылдамдық болып келеді. t уақыт мезетінде радиус-векторымен анықталатын М орнында, ал t₁ уақыт мезетінде радиус-векторымен анықталатын М₁ орнында болсын дейік (4.3 сурет). Сонда уақыт аралығында нүктенің орын ауыстыруы орын ауыстыру векторымен анықталады. ОММ₁ үшбұрышынан болатыны көрінеді, яғни . Орын ауыстыру векторының сәйкес уақыт аралығына қатынасы, нүктенің t уақыт аралығындағы модулі мен бағыты бойынша ортақ жылдамдығы деп аталатын векторлық шамасын береді, .

векторлық шамасы нүктенің t уақыт мезетіндегі жылдамдығы деп аталады, сонда нүктенің жылдамдығы векторының t аргументі бойынша бірінші ретті туындысы болып келеді

. (4.4)

Нүктенің үдеуі - оның жылдамдығының модулі мен бағытының уақыт өтуімен өзгеруін сипаттайтын векторлық шама. Әлдебір t уақыт мезетінде нүктенің орны М және жылдамдығы болсын, ал t₁ мезетінде нүкте M₁ орнына келіп, жылдамдығына ие болады дейік (4.4 сурет). Сонда 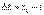уақыт аралығында нүктенің жылдамдығы өсімін алады, ол әрқашан траекториясының ойыс жағына бағытталады. векторының t аралығына қатынасы нүктенің сол ауқыт аралығындағы орташа үдеуін анықтайды. t нөлге ұмтылған кезде ұмтылатын векторлық шама

(4.5)

нүктенің берілген t уақыт мезетіндегі үдеуі деп аталады. Сонымен, нүктенің берілген уақыт мезетіндегі үдеу векторы жылдамдық векторының уақыт бойынша бірінші ретті туындысына, яғни нүктенің радиус-векторының екінші ретті туындысына тең.

Не нашли, что искали? Воспользуйтесь поиском: