Атты дененің тұрақты өс төңірегіндегі айналмалы қозғалысы

АҚД-нің тұрақты (қозғалмайтын) өс төңірегінде айналғанда, оның өсте жатқан нүктелері қозғалмайды (4.5 суретіндегі АВ). Өс арқылы екі жазықтық жүргізейік – қозғалмайтын және денемен байланысып қозғалатын жазықтықты. Олардың арасындағы екі жақтық  бұрышы дененің бұрылу бұрышы деп аталады, ол айналу өсінің оң бағыты жағынан қарағанда сағат тілінің қозғалысына қарсы болып көрінгенде, оң болып есептеледі. АҚД-нің тұрақты өс төңірегіндегі айналу заңы – келесі тәуелділік

 =  (t). (4.16)

Бұрыштық жылдамдық  бұрышының уақыт өтуімен өзгеруін сипаттайды

 = d/dt, яғни . (4.17)

Дененің бұрыштық жылдамдығын модулі || тең және айналу өсінің бойымен, ұшынан қарағанда дене сағат тілінің қозғалысына қарсы айналатын болып, бағытталған векторымен кескіндеуге болады.

Бұрыштық үдеу бұрыштық жылдамдығының уақыт өтуімен өзгеруін сипаттайды

 = d/dt = d² /dt², яғни . (4.18)

Егер қозғалыс кезінде =const болса, айналу бірқалыпты деп аталады. (4.17) формуласын интегралдап, айналу заңын анықтаймыз

(4.19)

Бірқалыпты айналу кезінде болса, онда

. (4.19’)

Егер қозғалыс кезінде бұрыштық үдеу тұрақты болса(=const), айналу бірқалыпты айнымалы деп аталады, оның заңы келесі түрде жазылады

. (4.20)

Егер  мен  таңбалары бірдей болса, айналу – бірқалыпты үдемелі, әртүрлі болса, бірқалыпты кемімелі болады.

Айналатын дене нүктелерінің жылдамдықтары мен үдеулерін анықтаймыз (4.6 сурет).

Айналу кезінде М нүктесі радиусы h тең, жазықтығы айналу өсіне перпендикуляр және P центрі өсте жататын шеңберді кескіндейді. dt уақыт ішінде дене dφ бұрышына бұрылады, М нүктесі ds = h∙ dφ орын ауыстыру жасайды. Сонда

. (4.21)

Нүктенің үдеулерін анықтаймыз

(4.22)

үдеуі траекторияға жанама бағытталады (үдемелі айналу кезінде айналу бағытына сәйкес және кемімелі айналу кезінде айналу бағытына қарсы), 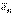үдеуі әрқашан МP радиусы бойымен өске қарай бағытталады. Нүктенің толық үдеуі

(4.23)

 бұрышы(4.6 сурет) келесі тәуелдік арқылы анықталады

. (4.24)

және векторлары үшін келесі формулуларды шығаруға болады

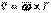, (4.25)

(4.26)

Не нашли, что искали? Воспользуйтесь поиском: