Бас инерция өстері мен бас инерция моменттері

x пен y координаттық өстерін u мен v орнына келтіріп бұрғанда, жазық қиманың инерция моменттері қалай өзгертінін қарастырайық. 10.4 суреттен келесіні анықтай аламыз

u = y∙ sin  + x ∙ cos ; v = y∙ cos   x∙ sin . (10.13)

Осы өрнектерді

, ,

ескерілуімен түрлендіріп, келесіге келеміз

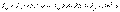, (10.14)

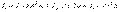, (10.15)

. (10.16)

Алдыңғы екі теңдеуді қосып, келесіні аламыз

(10.17)

Сонымен, өзара перпендикуляр өстерге қатысты өстік инерция моменттерінің қосындысы өстер бұрылғанда тұрақты болып қалады және жазық фигураның полюстік инерция моментіне тең.

(10.17) қолдануымен дөңгелек қиманың диаметріне қатысты өстік инерция моментін анықтауға болады. Симметрия себебінен , сонда

(10.18)

 бұрышы өзгеруімен 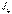және өзгереді, ал олардың қосындысы тұрақты болады, сондықтан олардың біреуін 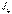немесе , өзінің максимал-ды мәніне, екіншісін минималды мәніне ие болдыратынбұрыштың =₀ мәнін табуға болады. ₀ табу үшін 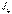немесе 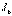экстремумге зерттейміз. Сонда келесі табылады

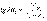. (10.19)

=₀ болғанда біржолы центрден тепкіш инерция моменті нөлге тең болатынын көрсетуге болады. Егер өстерге қатысты центрден тепкіш инерция моменті нөлге тең, ал өстік инерция моменттері экстремалды мәндерін алатын болса, онда сол өстер бас инерция өстері деп аталады. Бас инерция өстеріне қатысты өстік инерция моменттері бас инерция моменттері деп аталады. Олар (10.14), (10.15) және (10.19) қолдануымен келесідей табылады

. (10.20)

Жазық фигураның кез келген l өсіне қатысты инерция радиусы деп келесі формуламен анықталатын шаманы атайды

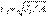. (10.21)

Не нашли, что искали? Воспользуйтесь поиском: