
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема №6 Дифференциальные уравнения 1 страница
1. Решить дифференциальные уравнения
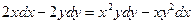  
| 2. Решить дифференциальные уравнения
  
|
Вопросы к зачету: Раздел 1. Линейная алгебра
Вопросы к теме №1
1. Понятие матрицы, основные виды.
2. Диагональная и единичная матрицы.
3. Треугольная матрица.
4. Операции над матрицами.
5. Сложение и умножение матриц на скаляр.
6. Транспонирование матриц.
7. Умножение матриц.
8. Обратная матрица.
Вопросы к теме №2
1. Понятие об определителе «n-го» порядка.
2. Вычисление определителей 2 и 3 порядка.
3. Минор и алгебраическое дополнение элемента матрицы.
4. Свойства определителей.
5. Разложение матрицы по строке (столбцу).
6. Простейшие матричные уравнения.
Вопросы к теме №3
1. Системы линейных алгебраических уравнений.
2. Решение системы, совместная и несовместная системы.
3. Метод Гаусса решения системы линейных алгебраических уравнений.
4. Метод Крамера решения системы линейных алгебраических уравнений.
5. Матричный метод решения системы линейных алгебраических уравнений.
6. Собственные числа и собственные векторы квадратных матриц.
7. Линейная модель торговли.
8. Модель Леонтьева.
9. Применение СЛАУ в экономических исследованиях.
Вопросы к теме №4
1. Вектор, координаты вектора.
2. Линейные операции над векторами.
3. Коллинеарные вектора.
4. Компланарные вектора.
5. Скалярное произведение векторов и его свойства.
6. Длина (норма) вектора.
7. Угол между векторами.
8. Векторное произведение и его свойства.
9. Смешанное произведение векторов и его свойства.
Вопросы к теме №5
1. Прямая на плоскости. Различные уравнения прямой на плоскости.
2. Расстояние от точки до прямой.
3. Взаимное положение прямых.
4. Угол между прямыми.
5. Прямая и плоскость в пространстве.
6. Условия параллельности и перпендикулярности прямых.
7. Кривые 2 порядка: окружность, эллипс, гипербола, парабола. Построение кривых 2 порядка.
8. Алгебраические поверхности 2 порядка (сфера, эллипсоид, параболоид).
Вопросы к экзамену: Раздел 2 Математический анализ
Тема № 1
1. Понятие множества, элемента множества. Пустое множество, подмножество. Равенство множеств. Операции над множествами: пересечение, объединение, разность.
2. Понятие функции. Способы задания. Функции, заданные параметрически.
3. Общие свойства функций: область определения, множество значений, четность, периодичность, нули функции, ограниченность, монотонность, наибольшее и наименьшее значения функции на множестве.
4. Сложная функция.
5. Классификация функций. Простейшие элементарные функции (графики, основные свойства). Функции в экономическом анализе.
6. Предел функций на бесконечности. Предел функции в точке. Односторонние пределы.
7. Понятие бесконечно малых и бесконечно больших функций.
8. Арифметические свойства пределов. Предел сложной функции.
9. Первый замечательный предел, его следствия.
10. Второй замечательный предел.
11. Различные определения непрерывности функций в точке. Точки разрыва, их классификация.
12. Асимптоты функций.
Тема №2
1. Определение производной функции в точке.
2. Производная суммы, разности, произведения частного функций.
3. Производные основных элементарных функций. Таблица производных. Производные высших порядков.
4. Вычисление производных неявно заданных функций.
5. Уравнения нормали и касательной плоскости к графику функции.
6. Дифференциал функции. Геометрический смысл производной и дифференциала. Производная и дифференциал сложной.
Тема №3
1. Правило Лопиталя.
2. Экстремум функции. Необходимое условие экстремума. Стационарные точки.
3. Достаточные условия экстремума.
4. Возрастание, убывание функции в точке. Достаточное условие.
5. Направления выпуклости графика функции. Признак.
6. Точки перегиба. Необходимые и достаточные условия перегиба.
7. Общая схема исследования функции и построения графиков.
8. Формула непрерывных процентов.
9. Эластичность спроса и предложения.
Тема №4
1. Понятие функции нескольких переменных.
2. Частные производные. Дифференцируемость функций многих переменных. Дифференциал.
3. Частные производные и дифференциалы высших порядков, теорема о равенстве смешанных производных.
4. Понятие экстремума функции нескольких переменных. Необходимые и достаточные условия. Случай двух переменных. Условный экстремум. Прямой метод отыскания условного экстремума.
5. Функции спроса и предложения. Функции полезности. Кривые безразличия
Тема №5
1. Понятие первообразной и неопределенного интеграла.
2. Основные свойства неопределенного интеграла.
3. Таблица интегралов. Приемы интегрирования: замена переменной, формула интегрирования по частям.
4. Понятие об интегрировании рациональных дробей. Задачи, приводящие к понятию определенного интеграла.
5. Определенный интеграл.
6. Производная определенного интеграла с переменным верхним пределом по этому пределу.
7. Приложения определенного интеграла. Интегральная теорема о среднем.
8. Вычисление площади криволинейной трапеции.
9. Вычисление длины кривой.
10. Понятие о несобственных интегралах. Определения. Формулы интегрального исчисления для несобственных интегралов. Признак сравнения.
Тема №6
1. Дифференциальные уравнения 1 порядка.
2. Дифференциальные уравнения с разделяющимися переменными.
3. Однородные дифференциальные уравнения 1 порядка.
4. Линейные дифференциальные уравнения 1 порядка. Уравнения Бернулли.
5. Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами.
6. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. Частные решения.
Рекомендуемая литература
Основная:
- Кремер Н.Ш. Высшая математика для экономистов, М.: ЮНИТИ, 2001.
- В.А. Абчук. Математика для менеджеров и экономистов. СПб.:Изд-во Михайлова В.А., 2002 г.
- В. И. Ермаков Сборник задач по высшей математике для экономистов. М.,ИНФРА-М, 2004.
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., ВШ., 2003.
- Гмурман В. Е. Теория вероятностей и математическая статистика. М., ВШ., 2003.
Дополнительная:
5. М.С.Красс, Б.П.Чупрынов, Основы математики и ее приложения в экономическом образовании, М.:Дело, 2001.
6. Шипачев B.C. Основы высшей математики. М.: Высш. шк.., 2001.
7. Шипачев B.C. Задачник по высшей математике. М.: Высш. шк.., 2001.
4. СЛОВАРЬ ТЕРМИНОВ (ГЛОССАРИЙ)
Матрицей размера  , где
, где  - число строк,
- число строк, 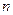 - число столбцов, называется прямоугольная таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются
- число столбцов, называется прямоугольная таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются  , где
, где  - номер строки, а
- номер строки, а  - номер столбца
- номер столбца 
Если число столбцов матрицы равно числу строк  , то матрица называется квадратной. Если
, то матрица называется квадратной. Если 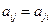 , то матрица называется симметрической.
, то матрица называется симметрической.
Квадратная матрица вида  называется диагональной матрицей.
называется диагональной матрицей.
Квадратная матрица вида  называется единичной матрицей. Единичная матрица обозначается символом
называется единичной матрицей. Единичная матрица обозначается символом 
Матрица, все элементы которой равны  , называется нулевой матрицей. Нулевая матрица обозначается символом
, называется нулевой матрицей. Нулевая матрица обозначается символом 
Суммой (разностью) матриц 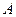 и
и  называется матрица
называется матрица  ,
,  элементами которой являются соответственно сумма (разность) элементов исходных матриц
элементами которой являются соответственно сумма (разность) элементов исходных матриц

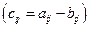 .
.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число

Произведением матрицы 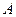 на матрицу
на матрицу  называется матрица
называется матрица  , элементы которой могут быть вычислены по формуле
, элементы которой могут быть вычислены по формуле
 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. Умножение матриц, вообще говоря, не коммутативно, т.е.  даже если определены оба произведения. Однако, если для каких - либо матриц равенство
даже если определены оба произведения. Однако, если для каких - либо матриц равенство  выполняется, то такие матрицы называются перестановочными.
выполняется, то такие матрицы называются перестановочными.
Матрицу  называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В другими словами, если
называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В другими словами, если  . Матрица, транспонированная матрице
. Матрица, транспонированная матрице 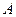 обозначается символом
обозначается символом 


Определителем (детерминантом) квадратной матрицы  называется число, которое может быть вычислено по элементам матрицы по формуле
называется число, которое может быть вычислено по элементам матрицы по формуле  , где
, где  – детерминант матрицы, полученной из исходной вычеркиванием первой строки и
– детерминант матрицы, полученной из исходной вычеркиванием первой строки и  – го столбца. Определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула
– го столбца. Определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула
 ,
, 
Определитель единичной матрицы равен 1. Для указанной матрицы А число  называется дополнительным минором элемента матрицы
называется дополнительным минором элемента матрицы  . Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено  строк и столбцов, то полученный минор называется минором порядка s.
строк и столбцов, то полученный минор называется минором порядка s.
Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы называется дополнительным минором.
Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на  в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Элементарными преобразованиями матрицы называются следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к одной строке другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование.
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов).
Если существуют квадратные матрицы Х и А одинакового порядка, удовлетворяющие условию  где
где  - единичная матрица того же порядка, то матрица
- единичная матрица того же порядка, то матрица 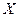 называется обратной по отношению к матрице А и обозначается
называется обратной по отношению к матрице А и обозначается 
Базисным минором матрицы порядка  называется минор порядка
называется минор порядка  , если он не равен нулю, а все миноры порядка
, если он не равен нулю, а все миноры порядка  и выше равны нулю, или не существуют вовсе, т.е. число
и выше равны нулю, или не существуют вовсе, т.е. число  совпадает с меньшим из чисел
совпадает с меньшим из чисел  или
или 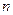 .
.
Столбцы и строки матрицы, на которых стоит базисный минор, называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Порядок базисного минора матрицы называется рангом матрицы. Элементарные преобразования не изменяют ранг матрицы.
Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Системой m линейных алгебраических уравнений относительно n неизвестных 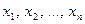 называется система
называется система

Решением системы m линейных алгебраических уравнений относительно n неизвестных 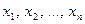 называется совокупность n значений неизвестных
называется совокупность n значений неизвестных 
 , при подстановке которых все уравнения системы обращаются в тождества.
, при подстановке которых все уравнения системы обращаются в тождества.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения - несовместной.
Если правая часть системы m линейных алгебраических уравнений относительно n неизвестных 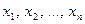 равна нулю, то система называется однородной.
равна нулю, то система называется однородной.
Система из  линейно независимых решений линейной однородной системы называется фундаментальной системой решений. Фундаментальная система решений образует базис в подпространстве решений линейной однородной системы.
линейно независимых решений линейной однородной системы называется фундаментальной системой решений. Фундаментальная система решений образует базис в подпространстве решений линейной однородной системы.
Общим решением линейной системы называется выражение, позволяющее вычислить все решения системы.
Комплексным числом 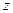 называется упорядоченная пара действительных чисел
называется упорядоченная пара действительных чисел 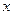 и
и 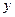 :
:  , где
, где 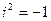 (число
(число  называется мнимой единицей).
называется мнимой единицей).
Комплексные числа 
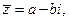 называются сопряженными друг другу.
называются сопряженными друг другу.
Пусть  - множество элементов, для которых определены операции сложения и умножения на число, причём эти операции обладают следующими свойствами. Для любых элементов
- множество элементов, для которых определены операции сложения и умножения на число, причём эти операции обладают следующими свойствами. Для любых элементов  ,
,  ,
,  из множества
из множества  выполняются законы
выполняются законы
1)  (коммутативность сложения);
(коммутативность сложения);
2)  (ассоциативность сложения);
(ассоциативность сложения);
3) во множестве  существует нулевой элемент
существует нулевой элемент  такой, что для любого элемента
такой, что для любого элемента  ,
,  (существование нулевого элемента);
(существование нулевого элемента);
4) для любого элемента  существует элемент
существует элемент  , такой, что
, такой, что  (существование противоположного элемента);
(существование противоположного элемента);
5) 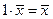 .
.
Для любых действительных чисел  любых элементов
любых элементов  ,
,  из множества
из множества  ;
;
6)  ;
;
7) Распределительный закон  ;
;
8)  .
.
Множество  называется линейным (векторным) пространством, а его элементы называются векторами.
называется линейным (векторным) пространством, а его элементы называются векторами.
Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.
Говорят, что в линейном пространстве  задано некоторое линейное преобразование А, если любому элементу
задано некоторое линейное преобразование А, если любому элементу  по некоторому правилу ставится в соответствие элемент
по некоторому правилу ставится в соответствие элемент 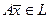 .
.
Преобразование А называется линейным, если для любых векторов  и
и  и любого
и любого  выполняются равенства
выполняются равенства 
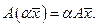
Линейное преобразование называется тождественным, если оно преобразует каждый элемент линейного пространства в себя  .
.
Если в пространстве  существуют векторы линейного преобразования
существуют векторы линейного преобразования  , то другой вектор
, то другой вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  .
.
Если 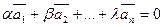 выполняется только при
выполняется только при 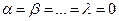 , то векторы
, то векторы  называются линейно независимыми.
называются линейно независимыми.
Если в линейном пространстве  есть n линейно независимых векторов, а любые
есть n линейно независимых векторов, а любые  векторов линейно зависимы, то пространство
векторов линейно зависимы, то пространство  называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства
называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства  .
.
Если вектор  переводится в вектор
переводится в вектор  линейным преобразованием с матрицей А, а вектор
линейным преобразованием с матрицей А, а вектор  в вектор
в вектор  линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор
линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор  в вектор
в вектор  (оно называется произведением составляющих преобразований).
(оно называется произведением составляющих преобразований).
Пусть  – заданное n - мерное векторное пространство. Ненулевой вектор
– заданное n - мерное векторное пространство. Ненулевой вектор  называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:
называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:  . При этом число
. При этом число 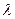 называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору
называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору  .
.
Если линейное преобразование А в некотором базисе  ,
, 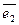 ,…,
,…,  имеет матрицу
имеет матрицу  , то собственные значения линейного преобразования А можно найти как корни
, то собственные значения линейного преобразования А можно найти как корни  уравнения:
уравнения:  .
.
Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом линейного преобразования А. Характеристический многочлен линейного преобразования не зависит от выбора базиса.
Однородный многочлен второй степени относительно переменных 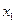 и
и 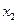
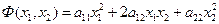 не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных 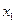 и
и 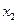 .
.
Однородный многочлен второй степени относительно переменных  и
и 
 ,
,
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных  и
и  .
.
Не нашли, что искали? Воспользуйтесь поиском: