Тема №6 Дифференциальные уравнения 4 страница

Точки локального максимума и локального минимума функции 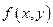называются точками экстремума этой функции. Рассмотрим функцию в точках и . Построим вектор . Углы наклона этого вектора к положительным направлениям координатных осей обозначим соответственно 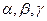. Косинусы этих углов называются направляющими косинусами вектора .

Предел называется производной функции по направлению вектора в точке с координатами .

Если в некоторой области D задана функция и некоторый вектор, проекции которого на координатные оси равны значениям функции 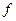в соответствующей точке , то этот вектор называется градиентом функции 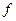. Обозначение

Дифференциальным уравнением называется уравнение, связывающее независимые переменные, неизвестные функции и производные различных порядков от неизвестных функций по независимым переменным.

Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

Общим решением дифференциального уравнения называется дифференцируемая функция одного или нескольких аргументов, которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Решение вида называется частным решением дифференциального уравнения.

Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида , удовлетворяющего начальным

Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

Интегральной кривой называется график решения дифференциального уравнения на плоскости .

Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности решения задачи Коши не выполняется, т.е. в окрестности некоторой точки 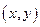существует не менее двух интегральных кривых.

Дифференциальным уравнением первого порядканазывается уравнение, связывающее неизвестную функцию, ее первую производную и независимую переменную, т.е. уравнение вида:. Если это уравнение преобразовать к виду, то полученное дифференциальное уравнение первого порядка называется уравнением, разрешенным относительно производной.

Дифференциальное уравнение 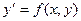называется уравнением с разделяющимися переменными, если его можно представить в виде: или в виде:

Функция 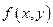называется однородной функцией n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Дифференциальное уравнение вида 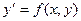называется однородным, если его правая часть 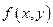есть однородная функция нулевого измерения относительно своих аргументов.

Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть представлено в виде: При этом, если правая часть уравнения равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением. Если правая часть уравнения не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. Причём 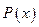и являются непрерывными функциями на некотором промежутке .

Дифференциальное уравнение первого порядка вида: 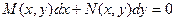называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции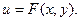

Уравнением Лагранжа называется дифференциальное уравнение, линейное относительно х и у, коэффициенты которого являются функциями от : .

Уравнением Клеро называется уравнение первой степени (т.е. линейное) относительно функции и аргумента вида:

Линия 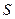, являющаяся графиком функции, определяющей некоторое решение дифференциального уравнения, называется интегральной кривой уравнения Производная называется угловым коэффициентом касательной к интегральной кривой.

Множество касательных в каждой точке рассматриваемой области называется полем направлений.

Линии равного наклона в поле направлений называются изоклинами.

Линейным дифференциальным уравнением n – го порядка называется уравнение первой степени относительно функции у и ее производных до 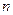- го порядка включительно вида: где – функции от х или постоянные величины, причем .

Если , то уравнение называется линейным однородным дифференциальным уравнением, если , то уравнение называется линейным неоднородным дифференциальным уравнением, если все коэффициенты – постоянные числа, то уравнение называется линейным дифференциальным уравнением порядка 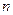с постоянными коэффициентами.

Выражение называется линейным дифференциальным оператором.

Фундаментальной системой решений линейного однородного дифференциального уравнения n –го порядка на интервале называется всякая система n линейно независимых на этом интервале решений уравнения.

Не нашли, что искали? Воспользуйтесь поиском: