Понятие погрешности измерений

Непосредственной задачей измерения является определение значений измеряемой величины. В результате измерения физической величины с истинным значением Х_и мы получаем оценку этой величины Х_изм – результат измерений. При этом следует четко различать два понятия: истинные значения физических величин и их эмпирические проявления – действительные значения, которые являются результатами измерений и в конкретной измерительной задаче могут приниматься в качестве истинных значений.

Истинное значение величины неизвестно и оно применяют только в теоретических исследованиях. Результаты измерений являются продуктами нашего познания и представляют собой приближенные оценки значений величин, которые находятся в процессе измерений. Степень приближения полученных оценок к истинным (действительным) значениям измеряемых величин зависит от многих факторов: метода измерений, использованных средств измерений и их погрешностей, от свойств органов чувств операторов, проводящих измерения, от условий, в которых проводятся измерения и т.д. Поэтому между истинным значением физической величины и результатом измерений всегда имеется различие, которое выражается погрешностью измерений (то же самое, что погрешностью результата измерений).

Погрешность результата измерения ∆ – отклонение результата измерения от истинного значения измеряемой величины: ∆ = X_изм – X_и.

Так как истинное значение измеряемой величины всегда неизвестно и на практике мы имеем дело с действительными значениями величин Х_д, то формула для определения погрешности в связи с этим приобретает вид: ∆ = X_изм – X_д.

Погрешность результата измерения имеет много составляющих, каждая из которых обусловлена различными факторами и источниками. Типичный подход к анализу и оцениванию погрешностей состоит в выделении этих составляющих, их изучении по отдельности и суммировании по принятым правилам. Определив количественные параметры всех составляющих погрешности и, зная способы их суммирования, можно правильно оценить погрешность результата измерений и при возможности скорректировать его с помощью введения поправок.

Ниже приводятся некоторые источники появления погрешностей измерений:

― неполное соответствие объекта измерений принятой его модели (идеализированный образ объекта измерений, соответствующие параметры которого можно наилучшим образом представить в качестве истинного значения измеряемой величины);

― неполное знание измеряемой величины;

― неполное знание влияния условий окружающей среды на измерение;

― несовершенное измерение параметров окружающей среды;

― конечная разрешающая способность прибора или порог его чувствительности;

― неточность передачи значения единицы величины от эталонов к рабочим средствам измерений;

― неточные знания констант и других параметров, используемых в алгоритме обработки результатов измерения;

― аппроксимации и предположения, реализуемые в методе измерений;

― субъективная погрешность оператора при проведении измерений;

― изменения в повторных наблюдениях измеряемой величины при очевидно одинаковых условиях и другие.

Группируя перечисленные выше и другие причины появления погрешностей измерений, их можно разделить на погрешности метода измерений, средств измерений (инструмента) и оператора, проводящего измерения. Несовершенство каждого этого компонента измерения вносит вклад в погрешность измерения. Поэтому в общем виде погрешность можно выразить следующей формулой:

∆ = ∆_м + ∆_и + ∆_л,

где ∆_м – методическая погрешность (погрешность метода); ∆_и – инструментальная погрешность (погрешность средств измерений); ∆_л – личная (субъективная) погрешность.

Методическая погрешность возникает из–за недостатков используемого метода измерений. Чаще всего это является следствием различных допущений при использовании эмпирических зависимостей между измеряемыми величинами или конструктивных упрощений в приборах, используемых в данном методе измерений.

Погрешности средств измерений могут быть обусловлены различными причинами:

― неидеальностью свойств средства измерений, то есть отличием его реальной функции преобразования от номинальной;

― воздействием влияющих величин на свойства средств измерений;

― взаимодействием средства измерений с объектом измерений – изменением значения измеряемой величины вследствие воздействия средства измерения;

― методами обработки измерительной информации, в том числе с помощью средств вычислительной техники.

Субъективная погрешность связана с такими индивидуальными особенностями операторов, как внимательность, сосредоточенность, быстрота реакции, степень профессиональной подготовленности. Такие погрешности чаще встречаются при большой доле ручного труда при проведении измерений и почти отсутствуют при использовании автоматизированных средств измерений.

Представленная классификация погрешностей измерений связана с причинами их возникновения. Кроме этого существуют и другие признаки, по которым классифицируются погрешности.

По характеру проявления (свойствам погрешностей) они разделяются на систематические и случайные, по способам выражения – на абсолютные, относительные и приведенные, по отношению к условиям применения – на основные и дополнительные.

Абсолютная погрешность ∆ выражается в единицах измеряемой величины, а относительная погрешность δ представляет собой отношение абсолютной погрешности к измеренному (действительному) значению величины и ее численное значение выражается либо в процентах, либо в долях единицы:

∆ = X_изм – X_д; δ = ∆ / X_д,

где X_изм – измеренное значение физической величины; X_д – действительное значение физической величины.

Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы. В этом случае пользуются понятием приведенной погрешности, равной отношению абсолютной погрешности измерительного прибора к некоторому нормирующему значению X_N:

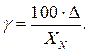
В качестве нормирующего значения принимается значение, характерное для данного вида измерительного прибора. Это может быть, например, диапазон измерений, верхний предел измерений, длина шкалы и т.д.

Рисунок 4 – Классификация погрешностей по характеру их проявления

Опыт проведения измерений показывает, что при многократных измерениях одной и той же неизменной физической величины при постоянных условиях погрешность измерений можно представить в виде двух слагаемых, которые по–разному проявляются от измерения к измерению. Существуют факторы, постоянно или закономерно изменяющиеся в процессе проведения измерений и влияющие на результат измерений и его погрешность. Погрешности, вызываемые такими факторами, называются систематическими.

Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессирующие, периодические, изменяющиеся по сложному закону.

Близость к нулю систематической погрешности отражает правильность измерений.

Систематические погрешности обычно оцениваются либо путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений, либо использованием более точных средств измерений. Как правило, систематические погрешности стараются исключить с помощью поправок. Поправка представляет собой значение величины, вводимое в неисправленный результат измерения с целью исключения систематической погрешности. Знак поправки противоположен знаку величины. Однако, поправки всегда определяются и вычисляются с некоторой погрешностью, часть систематических погрешностей так или иначе оказывается необнаруженной, поэтому существует понятие неисключенная систематическая погрешность(НСП). Иногда этот вид погрешности называют неисключенными остатками систематической погрешности, остающимися после введения поправок и содержащимися в результате измерений.

На возникновение погрешностей влияют также и факторы, нерегулярно появляющиеся и неожиданно исчезающие. Причем интенсивность их тоже не остается постоянной. Результаты измерения в таких условиях имеют различия, которые индивидуально непредсказуемы, а присущие им закономерности проявляются лишь при значительном числе измерений. Погрешности, появляющиеся в результате действия таких факторов, называются случайными погрешностями.

Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.

Незначительность случайных погрешностей говорит о хорошей сходимости измерений, то есть о близости друг к другу результатов измерений, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях и с одинаковой тщательностью.

Обнаруживаются случайные погрешности путем повторных измерений одной и той же величины в одних и тех же условиях. Они не могут быть исключены опытным путем, но могут быть оценены при обработке результатов наблюдений. Деление погрешностей измерений на случайные и систематические очень важно, т.к. учет и оценка этих составляющих погрешности требует разных подходов.

Факторы, вызывающие погрешности, как правило, можно свести к общему уровню, когда влияние их на формирование погрешности является более или менее одинаковым. Однако некоторые факторы могут проявляться неожиданно сильно, например, резкое падение напряжения в сети. В таком случае могут возникать погрешности, существенно превышающие погрешности, оправданные условиями измерений, свойствами средств измерений и метода измерений, квалификацией оператора. Такие погрешности называются грубыми, или промахами.

Грубая погрешность (промах) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных значений погрешности. Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных ошибок при проведении измерений. Если же причины появления резко выделяющихся наблюдений установить нельзя, то для решения вопроса об их исключении используют статистические методы.

Основная погрешность средства измерения – погрешность, определяемая при нормальных условиях применения СИ.

Дополнительная погрешность – составляющая погрешность СИ, дополнительно возникающая вследствие отклонения какой–либо из влияющих величин (температура, влажности, напряжение сети переменного тока и пр.) от её нормального значения.

Не нашли, что искали? Воспользуйтесь поиском: