Аналитическая геометрия на плоскости. Основным методом решения задач аналитической геометрии является метод координат.

Основным методом решения задач аналитической геометрии является метод координат.

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки на плоскости. Одной из таких систем является прямоугольная (декартова) система координат, которая задается двумя взаимно перпендикулярными прямыми-осями координат, на каждой из которых выбрано положительное направление и масштаб.

Координаты произвольной точки А в системе ОХУ записываются так: А(х;у).

Напомним наиболее важные формулы и уравнения аналитической геометрии, необходимые для решения задач.

Так, пусть даны две точк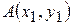и и

Тогда: 1)Расстояние между ними определяется по формуле:

. (2.1.1)

2) Координаты точки М (х,у), делящей отрезок АВ в отношении 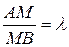, имеют вид:

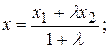
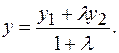(2.1.2)

3) В частности, координаты середины отрезка 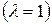находятся по формулам:

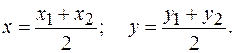(2.1.3)

4) Уравнение прямой, проходящей через две точки, имеет вид:

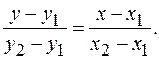(2.1.4)

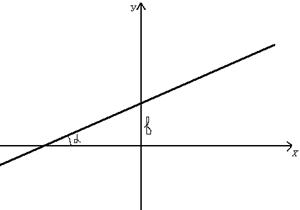
Уравнение прямой с угловым коэффициентом будет:

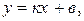(2.1.5)

где - угловой коэффициент или тангенс угла, образованного прямой с положительным направлением оси Ох; b – отрезок, отсекаемый прямой на оси Оу.

Угол между двумя прямыми, заданными своими уравнениями с угловыми коэффициентами 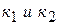, находится по формуле:

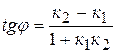. (2.1.6)

Из этой формулы легко получить условие параллельности и перпендикулярности 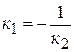прямых.

Во многих задачах используется уравнение прямой, проходящей через данную точку в данном направлении (уравнение пучка прямых):

, (2.1.7)

где (х 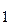,у 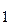) - координаты заданной точки (центр пучка).

Общее уравнение прямой на плоскости имеет вид:

Ах+Ву+С=0. (2.1.8)

Расстояние от точки А до прямой, заданной общим уравнением: Ах+Ву+С=0, находится по формуле:

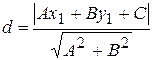. (2.1.9)

Пример 2.

Найти длину отрезка АВ, если известны координаты точек А(1;1) и В(4;5).

Решение:

Согласно формуле (2.1.1) будем иметь: подставим координаты точек А и В, получим: 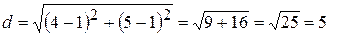(ед.дл.).

Пример 3.

Найти уравнение прямой, проходящей через точки А(1;2) и В(4;4) и ее угловой коэффициент.

Решение:

Используем уравнение (2.1.4): Подставим в него координаты точек А и В; ;

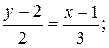
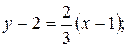
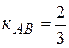- угловой коэффициент.

Пример 4.

Найти уравнение и длину перпендикуляра, опущенного из точки С(1;2) на прямую 3х – 4у + 2 =0.

Решение:

Через точку С проведем пучок прямых(2.1.7):

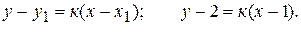
Угловой коэффициент «к» найдем из условия перпендикулярности прямых , для чего прежде найдем угловой коэффициент заданной прямой.

тогда .

Подставим найденное значение в уравнение пучка прямых.

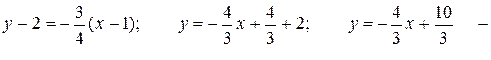уравнение перпендикуляра.

Длину этого перпендикуляра найдем по формуле(2.1.7):

где

- координаты точки С.

В нашем случае это будет: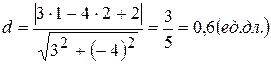

Пример 5.

Найти: а) уравнение медианы АЕ; б) прямой, проходящей через точку Е, параллельно стороне АВ в треугольнике с вершинами в точках А(-3;0),В(2;5) и С(4;3).

Решение:

а) Найдем координаты точки Е – середины отрезка ВС по формулам(2.1.3):

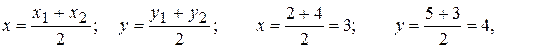Е(3;4).

Уравнение медианы найдем, используя уравнение прямой, проходящей через две точки(2.1.4).

Подставим в него координаты точек А и Е:

.

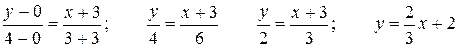б) Прежде, чем ответить на вопрос задачи, найдем уравнение стороны АВ, как прямой, проходящей через две точки. Затем через точку Е проведем пучок прямых, подчинив его условию параллельности прямых.

; .

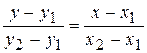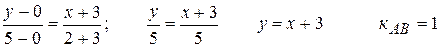Пучок прямых,. проходящих через точку Е: у-4=к (х-3).

Условие параллельности прямых . Подставим это значение «к» в уравнение пучка, у-4=х-3, или у=х+1.

Вопросы для самопроверки

1. Напишите формулы для вычисления расстояния между двумя точками и деления отрезка в данном отношении.

2. Как найти координаты середины отрезка?

3. Как найти угловой коэффициент прямой, если она задана общим уравнением?

4. Сформулируйте условия параллельности и перпендикулярности прямых.

5. Что представляет собой уравнение пучка прямых?

6. Напишите уравнение прямой, проходящей через две точки.

7. Как найти расстояние от точки до прямой?

Не нашли, что искали? Воспользуйтесь поиском: