Некоторые известные алгебраические неравенства

1. Неравенство о сумме двух взаимно обратных чисел:

1) Если a > 0 , то справедливо неравенство a + (1/a) ≥ 2,

причём неравенство обращается в равенство только при a = 1.

2) Если a < 0 , то справедливо неравенство a + (1/a) ≤ −2,

причём неравенство обращается в равенство только при a = −1.

Следствие. Если a и b – два числа одного знака, т.е. ab > 0, то справедливо неравенство а/b + b/а ≥ 2.

2. Соотношения между средними величинами

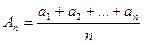– среднее арифметическое неотрицательных чисел а₁, а₂, …, а_n.

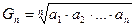– среднее геометрическое неотрицательных чисел а₁, а₂, …, а_n.

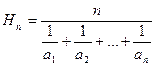– среднее гармоническое положительных чисел а₁, а₂, …, а_n.

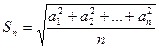– среднее квадратичное неотрицательных чисел а₁, а₂, …, а_n.

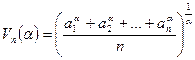– среднее степенное порядка a

положительных чисел а₁, а₂, …, а_n.

Большему значению a соответствует большее значение V_n(a).

0 ≤ min (a₁; a₂; …; a_n) ≤ H_n ≤ G_n ≤ A_n ≤ S_n ≤ max (a₁; a₂; …; a_n)

В частности, неравенство Коши между средним геометрическим и средним арифметическим: 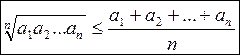, если а₁, а₂, …, а_n – неотрицательные числа

Для двух положительных чисел а и b справедливо:

0 ≤ min (a, b) £ £ £ £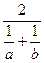

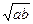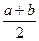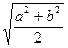
3. Неравенство Бернулли с натуральным показателем.

При любом действительном x ( x > −1) и при любом натуральном n справедливо неравенство

(1 + x)ⁿ ≥ 1+ nx.

4. Неравенство Бернулли с произвольным показателем.

Пусть x , r Î R, x > −1, r ≠ 0 , r ≠ 1. Тогда справедливы неравенства

(1 + x)^r ≤ 1+ xr, если 0 < r < 1,

(1 + x)^r ≥ 1+ xr, если r Ï [0,1],

причём неравенства обращаются в равенства только при x = 0.

5. Неравенство Бернулли для n чисел.

Пусть x₁, x₂,..., x_n ― числа одного знака, x_i > −1, i = 1, 2,..., n . Тогда

(1 + x₁)(1 + x₂)×…×(1 + x_n) ≥ 1+ x₁ + x₂ + ... + x_n.

6. Неравенство Коши–Буняковского.

Для любых действительных чисел a₁, a₂,..., a_n и b₁, b₂,..., b_n справедливо неравенство:

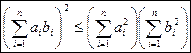, или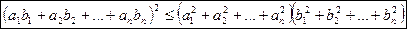

7. Свойства модуля

а) | x + y | £ | x | + | y | ; б) | x – y | ³ | x | – | y | .

Пример 3.

Сравнить два числа и 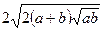, где a и b – неотрицательные числа, а ¹b.

Решение:

Преобразуем числа к виду

,

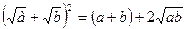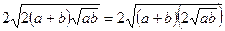
После деления обоих чисел на 2, приходим к неравенству между средними арифметическим и геометрическим для чисел (а + b) и .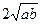

.

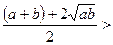
Таким образом, первое число больше.

Пример 4.

Пусть a + b + c = 1. Доказать справедливость неравенства a² + b² + c² ³ 1/3

для произвольных действительных чисел a, b, c.

Доказательство:

Воспользуемся неравенством Коши-Буняковского:

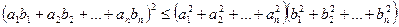
при n = 3, полагая а₁ = а, а₂ = b, a₃ = c и b₁ = b₂ = b₃ = 1.

1 = 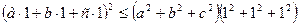=3(a² + b² + c²)

После деления последнего неравенства на 3 получаем исходное неравенство доказанным.

Не нашли, что искали? Воспользуйтесь поиском: