Задачи для самостоятельного решения. 1. Доказать, что х2 + у2 + z2 + u2 + a2 + a(x + y + z + u) ³ 0.

1. Доказать, что х ² + у ² + z ² + u ² + a ² + a (x + y + z + u) ³ 0.

2. Доказать, что а ⁴ + b ⁴ ³ 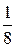, если а + b ³ 1.

3. Известно, что и х ₁ + х ₂ + …+ х ₆ = 0. Докажите, что .

4. Докажите, что для каждого x такого, что sin x ¹ 0, найдется такое натуральное n, что .

5. Докажите неравенство log₄5 + log₅6 + log₆7 + log₇8 ≥ 4,4.

6. Докажите неравенство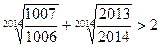

7. Для неотрицательных чисел х и у, не превосходящих 1, докажите, что

8. Докажите, что для любого x > 0 и натурального n выполнено неравенство

9. Сумма положительных чисел a, b, c равна π/ 2. Докажите, что

cos a + cos b + cos c > sin a + sin b + sin c.

10. Положительные числа x, y, z таковы, что модуль разности любых двух из них меньше 2. Докажите, что .

11. Доказать, что если а > 0, b > 0, с > 0, то .

12. Пусть a > c > 0, b > c. Доказать, что .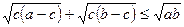

13. Доказать неравенство , где n – натуральное число, отличное от единицы.

14. Доказать неравенство , где n – натуральное.

15. Докажите, что если 1 < a < b < c, то log _a (log _ab) + log _b (log _bc) + log _c (log _ca) > 0.

16. Доказать, что , если х + у + z = 1 и каждое из чисел

х, у, z не меньше (–0,25).

17. Докажите, что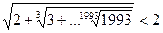

18. Доказать, что если a и b удовлетворяют линейному уравнению ах + by = c

с положительными коэффициентами, то .

19. Доказать, что если а ₁>0, a ₂>0,…, a_n >0, то

(а ₁+ а ₂+ а ₃+…+ а_n) .

20. Докажите, что если х ₁, х ₂, х ₃, х ₄, х ₅ – положительные числа, то

(х ₁ + х ₂ + х ₃ + х ₄ + х ₅)² ³ 4(х ₁ х ₂ + х ₂ х ₃ + х ₃ х ₄ + х ₄ х ₅ + х ₅ х ₁).

21. Докажите, что если a, b, c – положительные числа и ab + bc + ca > a + b + c,

то a + b + c > 3.

21. Докажите, что для любых неотрицательных чисел а и b справедливо неравенство: .

Не нашли, что искали? Воспользуйтесь поиском: