
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методические указания к решению
1. Построение эпюр внутренних силовых факторов (поперечной нагрузки и изгибающего момента)
Существует два способа определения внутренних усилий, возникающих в поперечных сечениях однопролетных статически определимых балок, одним из которых является построение эпюр этих усилий от действия на балки неподвижной нагрузки. Этот способ подробно рассматривается в курсе сопротивления материалов.
При определении значений внутренних усилий в балках предлагается пользоваться сформулированными ниже правилами.
Поперечная сила Q положительна, когда на левом торце правой части балки она направлена снизу вверх, а на правом торце левой части — сверху вниз.
Изгибающий момент М положителен, когда на левом торце правой части балки он направлен по часовой стрелке, а на правом торце левой части—против часовой стрелки.
При нагрузках, направленных не по нормали к оси балки (а под другим углом), в поперечных сечениях ее возникают кроме поперечных сил и изгибающих моментов также и продольные силы N.
Продольная сила положительна, когда она вызывает растяжение, и отрицательна, когда она вызывает сжатие.
На рис. 4. показаны положительные направления поперечной силы, продольной силы и изгибающего момента в поперечном сечении балки. Из рисунка видно, что при положительном изгибающем моменте верхние волокна балки испытывают сжатие (укорочение), а нижние – растяжение (удлинение); положительная поперечная сила вращает каждую часть балки относительно другого ее конца по часовой стрелке.

|
| Рис. 4. Положительные направления внутренних силовых факторов |
При построении эпюр поперечных и продольных сил положительные значения ординат откладывают вверх от оси эпюры, а отрицательные — вниз.
При построении же эпюры изгибающих моментов положительные значения их откладывают вниз от оси эпюры, отрицательные – вверх; в результате этого эпюры изгибающих моментов оказываются расположенными со стороны растянутых волокон балки.
Знак поперечной силы можно установить с помощью эпюры изгибающих моментов, используя следующее правило: поперечная сила в данном сечении положительна, если для совмещения оси элемента с касательной к эпюре изгибающих моментов приходится ось элемента вращать по часовой стрелке. Вращение оси должно происходить всегда так, чтобы угол поворота не превосходил 90°.
Поперечная сила Q равна (по величине и знаку) сумме проекций всех внешних сил, приложенных к левой части балки, на нормаль к ее оси, проведенную в рассматриваемом поперечном сечении, или сумме проекций (на ту же нормаль), взятой с обратным знаком, всех внешних сил, приложенных к правой части балки при этом проекции внешних сил на нормаль к оси балки положительны, когда они направлены снизу вверх.
 , (3)
, (3)
| где | Y – | проекция сил на нормаль к оси балки. |
Изгибающий момент М равен (по числовой величине и знаку) сумме моментов относительно оси z (проходящей через центр тяжести рассматриваемого поперечного сечения балки перпендикулярно плоскости действия внешних сил) всех внешних сил, приложенных к левой части балки, или сумме моментов, взятой с обратным знаком, всех внешних сил, приложенных к правой части балки, при этом моменты внешних сил положительны, когда они действуют по часовой стрелке.
 (4)
(4)
| где |  – –
| момент всех внешних сил относительно оси z. |
Продольная сила N равна (по числовой величине и знаку) сумме проекций всех внешних сил, приложенных к левой части балки, на ее ось или сумме проекций (на ту же ось), взятой с обратным знаком, всех внешних сил, приложенных к правой части балки. при этом проекции внешних сил на ось балки положительны, когда они действуют справа налево.
 (5)
(5)
| где | Х– | проекция внешних сил на ось Х |
Между эпюрами М и Q и нагрузкой, действующей на балку, существуют определенные зависимости. Эти зависимости позволяют проверять правильность эпюр и облегчают их построение. Они применимы не только для балок, но и для рамных систем, а потому имеют большое значение при расчете балочных конструкций.
Основная зависимость имеет вид:
 (6)
(6)
т. е. поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки (теорема Журавского).
Аналогично между поперечной силой и интенсивностью нагрузки существует также дифференциальная зависимость:
 (7)
(7)
Учитывая эти зависимости, можно сформулировать ряд положений:
- участкам с восходящими (слева направо) ординатами эпюры М (т. е. с убывающими значениями М) соответствуют участки с отрицательными значениями Q, а участкам с нисходящими ординатами эпюры М — участки с положительными значениями Q;
- чем круче касательная к эпюре М, тем больше абсолютное значение Q. Числовое значение поперечной силы равно «тангенсу» угла между этой касательной и осью балки;
- в сечениях, где поперечная сила равна нулю, изгибающий момент максимальный или минимальный;
- между сосредоточенными силами (если между ними отсутствует распределенная нагрузка) эпюра М ограничена прямой (в общем случае наклонной), а эпюра Q — прямой горизонтальной линией;
- на участках балки с равномерно распределенной нагрузкой
эпюра М ограничена параболой второй степени, а эпюра Q – наклонной прямой;
- при распределенной нагрузке эпюра М обращена выпуклостью в ту сторону, в которую направлена эта нагрузка;
- точки приложения сосредоточенных сил, перпендикулярных оси балки, соответствуют переломам в эпюре М и скачкам в эпюре Q. Когда сила направлена вниз, то и скачок в эпюре Q при перемещении слева направо должен быть вниз; когда сила направлена вверх, то и скачок должен быть вверх; величина скачка равна величине силы;
- изменение числового значения величины изгибающего момента на каком-либо участке балки равно площади эпюры поперечных сил на этом участке (при условии, что на данном участке к балке не приложены внешние моменты);
- изменение числового значения величины поперечной силы на каком-либо участке балки равно площади эпюры распределенной нагрузки q на этом участке.
1 Построение линий влияния внутренних силовых факторов (поперечной нагрузки и изгибающего момента) в конкретном сечении.
Линию влияния необходимо отличать от эпюры. Это по существу противоположные друг другу понятия. Ординаты эпюры характеризуют распределение изучаемого фактора (например, изгибающего момента) по различным сечениям балки при неподвижной нагрузке; ординаты же линии влияния, наоборот, характеризуют изменение фактора (например, того же момента), возникающего в одном определенном сечении при силе Р=1, перемещающейся по длине балки.
Рассмотрим принцип построения линий влияния.
а) Построение линий влияния опорных реакций.
Пусть по рассматриваемой балке перемещается груз Р = 1. Обозначим расстояние от левого края балки до груза через х. Это расстояние при перемещении груза будет меняться от нуля, когда груз стоит на левом краю балки до l, когда груз стоит на правом краю балки. Необходимо определить величину опорных реакции R1 и R2 в зависимости от расстояния х. Для этого нужно приравнять нулю сумму моментов всех сил относительно точек 1 и 2. Выразив значения опорных реакций R1 и R2 через переменную х получим уравнение, которым устанавливается закон изменения величины реакций в зависимости от положения груза Р = 1. Изобразив этот закон графически, получим линии влияния опорных реакций R1 и R2.
б) Построение линий влияния изгибающего момента и поперечной силы для некоторого сечения n.
Мысленно разрежем балку в сечении n и отбросим левую часть. В сечении n со стороны отброшенной части действует момент Mn и сила Qn, которые необходимо определить при различных положениях груза Р=1, то есть рассмотреть 2 случая – когда сила Р=1 находится левее сечения n и когда сила Р=1 находится правее этого сечения
2 Определение внутренних усилий (изгибающего момента и поперечной силы) в сечениях балки по линиям влияния.
Определение усилий по линиям влияния осуществляется при помощи формулы влияния:
S = M·tg α+ F·y + q·ω, (8)
| где | М – | сосредоточенный момент («+» - направлен по часовой стрелке, «-» - направлен против часовой стрелки); |
| α – | наклон линии влияния в месте приложения М; | |
| F – | сосредоточенная сила («+» - направлена вниз, «-» - направлена вверх); | |
| y – | ордината линии влияния над силой; | |
| q – | интенсивность распределенной нагрузки («+» - направлена вниз, «-» - направлена вверх); | |
| ω – | площадь линии влияния под нагрузкой |
При определении усилий по линиям влияния следует помнить, что внешний сосредоточенный момент вносится в формулу влияния со знаком «+», если направлен по часовой стрелке, внешняя сосредоточенная сила и распределенная нагрузка со знаком «+», если направлены вниз. Такие правила приняты при выводе формулы влияния. Знак же тангенса определяется обычным образом, т.е. в первой и третьей четвертях он положительный (если линия влияния не перевернута).
Пример решения
Исходные данные:
а=2 м; b=2 м; с=2 м; d=2 м; M=8 кН·м; F=2 кН; q=1 кН/м.

Решение.
1. Эпюры внутренних силовых факторов
а) Определение реакции в опорах рассматриваемой балки (Рис.5.)

Рис. 5.
Реакции R1 и R2 могут быть определены из условия, что сумма моментов всех сил относительно любой точки на оси балки должна равняться 0. Запишем выражения для суммы моментов всех сил относительно точек 1 и 2.


Далее необходимо рассмотреть каждый участок балки в отдельности:
Участок 1.
0<x<2 (Рис.6.)
Запишем выражения суммарного момента всех сил относительно левого и правого краев балки, откуда затем можно выразить значения для неизвестных силовых факторов (Q1 и М1) со стороны отброшенной части:


Аналогично рассматриваются последующие участки.
Участок 2.
2<x<4 (Рис.7.)

| 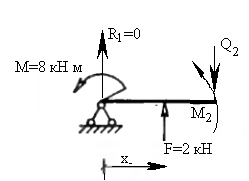
|
| Рис.6. | Рис.7. |





Подставим в полученные выражения значения х, соответствующие границам рассматриваемого участка:
- при х=2: М2 = -8кН·м; Q2 = 2 кН;
- при х=4: М2 = -4 кН·м; Q2 = 2 кН.
Участок 3.
4<x<6






Подставим в полученные выражения значения х, соответствующие границам рассматриваемого участка:
- при х=4: М3 = -4 кН·м; Q3 = 2 кН;
- при х=6: М3 = -2 кН·м; Q3 = 0 кН.
Участок 4.
6<x<8








Подставим в полученные выражения значения х, соответствующие границам рассматриваемого участка:
- при х=6: М4 = -2 кН·м; Q4 = 2 кН;
- при х=8: М4 = 0 кН·м; Q4 = 0 кН.
Таким образом, эпюры внешних силовых воздействий рассматриваемой балки имеют следующий вид (рис. 8):

Рис.8.
2. Линии влияния внутренних силовых факторов в сечениях n и k.
а) Линии влияния опорных реакций (Рис. 9)

Рис. 9.
Определим величину опорных реакции R1 и R2 в зависимости от расстояния х из условия равенства 0 суммы всех моментов относительно любой точки на оси балки.


Так как переменная х входит в уравнения в первой степени, то линия влияния будет прямолинейной. Построим Линии влияния опорных реакций для рассматриваемой балки (Рис.10.)

Рис.10.
б) Линии влияния изгибающего момента и поперечной силы для сечения n, находящегося на расстоянии 2 от левой опоры
Мысленно разрежем балку в сечении n и отбросим левую часть. В сечении n со стороны отброшенной части действует момент Mn и сила Qn (Рис.11).

Рис.11.
Пока груз находится левее сечения n (x<2) суммарный момент правой части балки относительно сечения n состоит только из момента Mn и момента опорной реакции R2.
При x<2: 
Когда же груз P=1 находится правее сечения n (x>2), суммарный момент в сечении n состоит из суммы моментов опорной реакции R2.и силы Р=1, а также момента Мn, действующего со стороны отброшенной части.
При x>2: 

Аналогично получим выражения для силы Qn. Поперечная сила, действующая в данном сечении, равна алгебраической сумме проекций внешних на нормаль к оси балки. Соответственно можно записать, что
При x<2: 
При x>2: 
Построим линии влияния момента и поперечной силы в сечении n (Рис.12).

Рис.12.
3. Определение внутренних усилий S (изгибающего момента или поперечной силы) в сечениях n и k по формуле влияния (8):
Мn = (-8) · (4/6) + (-2) · (4/3) + 1· 0 = -8 кН · м,
Qn = (-8) · (-1/6) + (-2) · (2/3) + 1 · 0 = 0 кН,
Мk = (-8) · 0 + (-2) · 0 + 1 · (-2) = -2 кН · м,
Qk = (-8) · 0 + (-2) · 0 + l · 2 = 2 кН.
Вывод: Значение усилий совпали с соответствующими усилиями на эпюре.
Не нашли, что искали? Воспользуйтесь поиском: