
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«МАТИ- РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ имени К.Э. ЦИОЛКОВСКОГО»
Кафедра «Моделирование систем и информационные технологии»
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Методические указания к практическим занятиям
по дисциплине «Математика»
Составители: Егорова Ю.Б.
Мамонов И.М.
МОСКВА 2011
ВВЕДЕНИЕ
Методические указания предназначены для студентов дневного и вечернего отделений факультета № 14 направлений подготовки бакалавров 150100.62, 160700.62, 220700.62, 230100.62.
Методические указания служат методической основой для практических занятий и выполнения индивидуальных заданий.
БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1.1. Биномиальный закон распределения появляется, если испытания проводятся по схеме Бернулли.
Пусть случайная величина Х -число появлений события А m раз в n испытаниях с одной и той же вероятностью Р(А)=р. Вероятность того, что событие А появится m раз в n испытаниях определяется по формуле Бернулли:
Р(Х=m)=Pn(m)= Cnm pm qn-m,
где m = 0, 1, 2,…, n; q = 1- p.
Дискретная случайная величина Х имеет биномиальный закон распределения, если она принимает значения 0, 1, 2,…, m,…, n cвероятностями P(Х=m), определенными по формуле Бернулли.
1.2. Ряд распределения биномиального закона имеет вид:
| X | … | m | … | n | ||
| P | qn | Cn1p qn-1 | … | Cnmpmqn-m | … | pn |
1.3. Согласно таблице, можно записать функцию распределения биномиальной случайной величины:
F(X) = 0, хЈ 0

F(X)= 1, x>n.
1.4. Если m и n -большие числа, то вероятность Р(Х=m) можно приблизительно вычислить с помощью локальной теоремы Муавра-Лапласа:
Если вероятность наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n, приближенно равна:
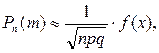
где функция  а аргумент
а аргумент 
Чем больше n, тем точнее вычисление Р(X=m). Поэтому теорему Муавра-Лапласа целесообразно применять при npq³ 20.
Для нахождения значений функции f(x) составлены специальные таблицы (например, см. приложение 1 в учебнике [1] или задачнике [2]). При использовании таблицы необходимо иметь в виду свойства функции f(x):
1) Функция f(x) является четной f(-x)= f(x).
2) При х ®∞ функция f(x) ®0 (практически можно считать, что уже при х >4 функция f(x) ≈0).
1.5. Mатематическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления cобытия в одном испытании:
M(X) = np.
Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления p и непоявления q события в одном испытании:
D(X) = npq.
1.6. Биномиальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.
Примеры дискретных случайных величин, имеющих биномиальный закон распределения: число бракованных деталей в крупной партии, число попаданий при стрельбе, число выпадения герба при многократном подбрасывании монеты и т.п.
ПРИМЕР 1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить ряд распределения числа отказавших элементов в одном опыте. Определить математическое ожидание и дисперсию.
Решение. Дискретная случайная величина Х -число отказавших элементов в одном опыте - имеет следующие возможные значения:
х1 = 0 (ни один из элементов устройства не отказал);
х2 = 1 (отказал один элемент);
х3 = 2 (отказали два элемента);
х4 = 3 (отказали три элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию n = 3; p =0,1 (следовательно, q = 1 -0,1 = 0,9), получим:
P 3(0) = q3= 0,93 = 0,729;
P 3(1) = C31 p1 q2 = 3Ч0,1Ч0,92 = 0,243;
P 3(2) = C32 p2 q1= 3Ч0,12Ч0,9 = 0,027;
P 3(3)= p 3= 0,13 = 0,001.
Напишем искомый биномиальный закон распределения Х:
| X | ||||
| P | 0,729 | 0,243 | 0,027 | 0,001 |
Контроль: 0,729+0,243+0,027+0,001 = 1.
Математическое ожидание:
М(Х) = nЧp = 3Ч0,1= 0,3 элемента.
Дисперсия:
D(X) = npq = 3Ч0,1Ч0,9 = 0,27 (элемента)2.
ПРИМЕР 2. Найти дисперсию дискретной случайной величины Х – числа появления события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы, и известно, что
М(Х) =1,2.
Решение. Воспользуемся формулой: М(Х) =np. По условию М(Х) =1,2; n =2. Следовательно, 1,2 = 2 p. Отсюда р = 0,6 и q =0,4.
Найдем искомую дисперсию:
D(X) = npq = 2Ч0,6Ч0,4 =0,48.
ПРИМЕР 3. Производится три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Рассматривается случайная величина Х – число появлений события А в трех опытах. Найти закон распределения (ряд распределения, многоугольник распределения, функцию распределения) случайной величины Х. Определить ее числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение, моду).
Решение. Дискретная случайная величина Х имеет следующие возможные значения:
х1 = 0 (событие А не появилось ни в одном из трех опытов);
х2 = 1 (событие А появилось в одном из трех опытов);
х3 = 2 (событие А появилось в двух опытах);
х4 = 3 (событие А появилось во всех трех опытах).
Соответствующие вероятности находим по формуле Бернулли (n = 3; p = 0,4; q = 1 – 0,4 = 0,6):
P 3(0) = q3= 0,63 = 0,216;
P 3(1) = C31 p1 q2 = 3Ч0,4Ч0,62 = 0,432;
P 3(2) = C32 p2 q1= 3Ч0,42Ч0,6 = 0,288;
P 3(3)= p3= 0,43 = 0,064.
Составим ряд распределения:
| X | ||||
| P | 0,216 | 0,432 | 0,288 | 0,064 |
Контроль: 0,216+0,432+0,288+0,064 = 1.
Многоугольник распределения приведен на рис. 1.

 pi
pi
0,5
 |
 0,25
0,25
 |


0 1 2 3 xi
Рис. 1. Многоугольник распределения
На основе ряда распределения находим функцию распределения:
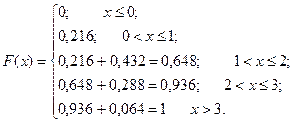
График F(x) приведен на рис. 2.
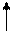
 F(x)
F(x)


 1
1


 0,936
0,936


 0,648
0,648
 |
 0,216
0,216


 0 1 2 3 xi
0 1 2 3 xi
Рис. 2. График функции распределения F(x)
Искомое математическое ожидание определяем по формуле:
M(X) = np = 3Ч0,4 = 1,2.
Найдем дисперсию:
D(X) = npq = 3Ч0,4Ч0,6 = 0,72.
Найдем среднее квадратическое отклонение:
s(Х)=  = 0,85.
= 0,85.
Мода: Мо =1.
Не нашли, что искали? Воспользуйтесь поиском: