
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЗАКОН РАСПРЕДЕЛЕНИЯ ПУАССОНА
2.1. Дискретная случайная величина Х имеет распределение Пуассона, если она принимает значения 0, 1, 2,…, m,…, n cвероятностями:
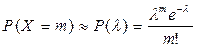 ,
,
где P(λ) -функция Пуассона; m = 0, 1, 2,…, m, …n; λ -параметр распределения. λ=np - среднее число появления события А в n испытаниях.
Значения Р(Х=m) можно определить по таблицам распределения Пуассона в зависимости от λ и m (например, см. табл. 3 в учебнике [7]).
2.2. Ряд распределения Пуассона имеет вид:
| X | … | m | … | n | ||
| P |  е - l е - l
| lе - l | … | 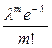
| … | 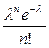
|
2.3. Согласно таблице можно записать функцию распределения случайной величины, распределенной по закону Пуассона:
F(х) = 0, хЈ 0;
 ;
;
F(х)= 1, x>n.
2.4. Mатематическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона:
M(X) = D(Х) = λ=np.
2.5. Закон распределения Пуассона может возникнуть в двух случаях:
1) При описании редких явлений, когда вероятность события А очень мала и стремится к нулю, а число опытов n велико (p →0, n →∞). В этом случае закон распределения Пуассона является предельным случаем биномиального закона и на практике применяется при условиях: n ≥10, p ≤0,1 и λ=np <10.
2) При описании событий, происходящих в определенные промежутки времени или в пространстве.
Примеры дискретных случайных величин, имеющих закон распределения Пуассона: число бракованных деталей в большой партии, число дорожно-транспорных происшествий, число пожаров, число отказов аппаратуры, число вызовов на телефонной станции за определенное время, число частиц, испускаемых радиоактивным источником за определенный промежуток времени и т.п.
ПРИМЕР 4. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Составьте ряд распределения числа поврежденных изделий.
Решение. Случайная величина Х -число поврежденных изделий -имеет распределение Пуассона с параметром λ=np= 5000∙0,0002=1<10.
Значения Р(Х=m) можно найти по таблице распределения Пуассона. Тогда ряд распределения имеет вид:
| X | … | |||||||||
| P | 0,3679 | 0,3679 | 0,1839 | 0,0613 | 0,0153 | 0,0031 | 0,0005 | 0,0001 | … | 0,000 |
ПРИМЕР 5. Нефтеразведывательная компания получила финансирование для проведения 6 нефтеразработок. Вероятность успешной нефтеразработки 0,05. Предположим, что нефтеразработку осуществляют независимые друг от друга разведывательные партии. Составьте ряд распределения числа успешных нефтеразработок. Найдите числовые характеристики этого распределения. Запишите в общем виде функцию распределения и постройте ее график.
Решение. Случайная величина Х -число успешных нефтеразработок -может иметь или биномиальное распределение, или распределение Пуассона с параметром λ=np= 6∙0,05=0,3<10.
Значения Р(Х=m) можно найти по таблице распределения Пуассона. Тогда ряд распределения имеет вид:
| X | |||||||
| P | 0,7408 | 0,222 | 0,0333 | 0,0033 | 0,0002 | 0,000.. | 0,000… |
На основе ряда распределения находим функцию распределения:
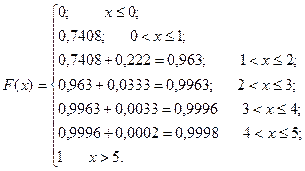
График F(x) приведен на рис. 3.
Числовые характеристики:
M(X) = λ=np = 0,3 разработки;
D(Х) = λ=np = 0,3 (разработки)2;
s(Х)= 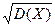 = 0,5477 разработки;
= 0,5477 разработки;
Мо =0 разработок.
 F(x)
F(x)







 1,0
1,0



 0,5
0,5
 |

 0 1 2 3 4 5 6 xi, кол-во разработок
0 1 2 3 4 5 6 xi, кол-во разработок
Рис. 3. График функции распределения F(x)
ПРИМЕР 6. Среднее число инкассаторов, прибывающих утром на автомобиле в банк в 15-минутный интервал, равно 2. Прибытие инкассаторов происходит случайно и независимо друг от друга. Составьте ряд распределения числа инкассаторов, прибывающих в банк в течение 15 мин. Найдите числовые характеристики этого распределения. Запишите в общем виде функцию распределения и постройте ее график.
Решение. Случайная величина Х -число инкассаторов -имеет распределение Пуассона с заданным параметром λ=np= 2 (среднее число инкассаторов, прибывающих в банк в определенный промежуток времени). Возможные значения случайной величины Х: 0, 1, 2,…, n.
Значения Р(Х=m) можно найти по таблице распределения Пуассона. Тогда ряд распределения имеет вид:
| X | … | |||||||||||
| P | 0,1353 | 0,2707 | 0,2707 | 0,1804 | 0,0902 | 0,0361 | 0,0120 | 0,0034 | 0,0009 | 0,0002 | 0,000 | … |
На основе ряда распределения находим функцию распределения:

График F(x) приведен на рис. 4.
Числовые характеристики:
M(X) = λ = 2 инкассатора;
D(Х) = λ = 2 (инкассатора)2;
s(Х)= 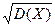 = 1,4142 инкассатора;
= 1,4142 инкассатора;
Мо1 =1 инкассатор; Мо2 =2 инкассатора.
 F(x)
F(x)






 1,0
1,0




 |
 0,5
0,5

 |
 0 1 2 3 4 5 6 7 8 9 xi, чел
0 1 2 3 4 5 6 7 8 9 xi, чел
Рис.4. График функции распределения F(x).
3. ГИПЕРГЕОМЕТРИЧЕСКИЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
3.1. Гипергеометрическое распределение представляет собой модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов, причем М объектов обладают определенным свойством А.
Пусть из N объектов извлекаются (без возврата) n объектов, причем m объектов обладают свойством А. Тогда случайная величина Х -число объектов, имеющих свойство А, -принимает значения: 0, 1, 2, …, m, …, n.
3.2. Для вычисления вероятностей Р(Х=m) формула Бернулли неприменима, так как отобранный объект не возвращается в исходную совокупность перед отбором следующего. Вероятность того, что m объектов имеют свойство А можно определить по формуле:
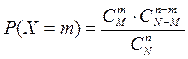
Ряд распределения имеет вид:
| X | … | m | … | n | ||
| P | 
| 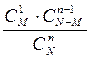
| … | 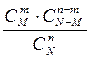
| … | 
|
3.3. Согласно таблице, можно записать функцию распределения случайной величины, распределенной по гипергеометрическому закону:
F(х) = 0, хЈ 0;
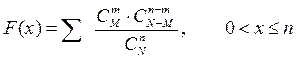
F(х)= 1, x>n.
3.4. Mатематическое ожидание и дисперсия случайной величины, распределенной по гипергеометрическому закону:

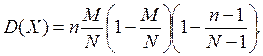
3.5. Гипергеометрический закон распределения широко используется в практике статистического приемочного контроля качества продукции, в задачах, связанных с организацией выборочных исследований, и в других областях.
Примеры дискретных случайных величин, имеющих гипергеометрический закон распределения: число бракованных деталей в небольшой партии; число неточных приборов в партии; число студентов, изучающих немецкий язык, в группе, изучающей два или более иностранных языка, и т.п.
ПРИМЕР 7. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны 2 детали. Составить ряд распределения числа стандартных деталей среди отобранных.
РЕШЕНИЕ. Случайная величина Х – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х1 =0, х2 =1, х3 =2. Вероятности этих возможных значений:
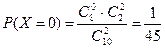
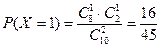
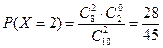
Составим искомый ряд распределения:
| Х | |||
| P | 1/45 | 16/45 | 28/45 |
Контроль: 1/45+16/45+28/45=1.
Не нашли, что искали? Воспользуйтесь поиском: