Уточненный расчет валов. Валы и шпиндели металлорежущих станков, как правило, имеют значительную длину из-за наличия в механизмах большого количества подвижных в осевом направлении

Валы и шпиндели металлорежущих станков, как правило, имеют значительную длину из-за наличия в механизмах большого количества подвижных в осевом направлении зубчатых колес (блоков зубчатых колес). Поэтому необходимо выполнить проверочные расчеты валов на прочность с учетом действующих на валы изгибающих моментов, вызванных силами в зубчатых передачах, а также расчеты валов на выносливость с учетом концентраторов напряжений. Методы таких расчетов подробно излагаются в курсах «Основы конструирования машин» и «Детали машин». Поэтому в данном учебном пособии приведены только особенности расчетов применительно к приводам металлорежущих станков.

При известных нагрузках на валы эти расчеты можно произвести, составив расчетную схему каждого вала.

ДОБАВИТЬ РАСЧЕТ С УЧЕТОМ ИЗГИБАЮЩИХ СИЛ ОТ ЗУБЧАТЫХ КОЛЕС.

В силу конструктивных особенностей валов напряжения, возникающие в каждой точке вала, меняются как по величине, так и по знаку. Это обстоятельство является главной причиной усталостного разрушения валов, поэтому расчет их усталостной прочности (выносливости) является основным.

Расчет на выносливость базируется на статическом расчете напряженно-деформированного состояния.

Расчетный запас прочности определяется для наиболее опасного сечения, поэтому, прежде всего, нужно найти те сечения вала, которые подлежат проверке. На рис.6.1. показаны наиболее часто встречающиеся примеры сечений:

- сечение 1—1, в котором имеется концентратор напряжений в виде галтели;

- сечение 2—2, ослабленное шпоночным пазом в месте приложения внешних сил F_t1, F_r1, F_a1 и моментов М_a1, T₁;

- сечение 3—3 с канавкой А;

- сечение 4—4, имеющее шпоночный паз в месте приложения внешних сил F_t2, F_r2, F_a2 и моментов М_a2, T₂.

Для каждого из этих сечений необходимо провести расчет усталостной прочности при совместном действии напряжений кручения и изгиба:

;

где — коэффициент запаса сопротивления усталости по изгибу;

— коэффициент запаса сопротивления усталости по напряжениям сдвига;

- s _am и t _am — амплитуды переменных напряжений;

- s _m и t _m — средние напряжения цикла;

- y_s и y_t — коэффициенты асимметрии цикла, учитывающие влияние средних напряжений на величину усталостной прочности; величины этих коэффициентов, согласно ГОСТ 25.504-82, рекомендуется выбирать следующим образом:

- y_s =0,02+2×10^-4s _b =0,02+2×10^-4×700=0,16;

- y_t =0,5 y_s =0,08;

- K_sD и K_tD — коэффициенты концентрации напряжений в опасном сечении при изгибе и кручении соответственно:

- K_sD =[(K_s/ K_ds) +1/ K_Fs -1 ] /K_n;

- K_tD =[(K_t/ K_dt) +1/ K_Ft -1 ] /K_n.

Рис.6.1. Примеры опасных сечений вала

Для получения числовых значений K_sD и K_tD необходимо рассчитать ряд параметров:

- K_s и K_t — эффективные коэффициенты концентрации напряжений, учитывающие влияние местных напряжений на величину запаса по усталостной прочности;

- K_ds и K_dt — масштабные факторы, характеризующие повышение вероятности появления усталостных трещин при возрастании линейных размеров детали, вычисляющиеся по формулам:

, ,

где d — выраженный в миллиметрах диаметр вала,

n_s = 0,19-1,25·10^-4·s _b = 0,19-1,25·10^-4·700 = 0,103;

n_t =l,5n_s = 0,155;

- K_Fs и K_Ft — коэффициенты влияния качества (шероховатости) поверхности, для тонкого шлифования равные K_Fs = K_Ft = 1;

- K_n — коэффициент, учитывающий наличие поверхностного упрочнения, равный для заданного вала K_n = 1, поскольку последний изготовлен без поверхностного упрочнения.

В этом случае расчетные формулы для вычисления коэффициентов концентрации напряжений в опасном сечении значительно упрощаются:

K_sD = K_s/ K_ds; K_tD = K_t/ K_dt.

Учитывая характер работы вала, можно, если противное не оговорено особо, закон изменения вызванных изгибом нормальных напряжений считать симметричным, а сжатием и растяжением по отношению к изгибу пренебречь.

При таких допущениях:

s _m = 0, s _am = M/W,

где М = — результирующий изгибающий момент; W — осевой момент сопротивления.

Касательные напряжения, в свою очередь, всегда положительны и могут изменяться пульсационно от нуля до номинального значения, поэтому:

t _m = t _am 0,5 t= T/2W_p,

Пример расчета.

Выполнить расчет вала (рис.6.2.) на сопротивление усталости, приняв:

Т₁, = Т₂, = 2000 Н-м; F_t1= 13,3 кН; F_t2 = 40 кН;

F_r1 = 4,9 кН; F_r2 = 14,7 кН; М_а1 = М_а2 = 280 Н-м;

F_al = 1,87 кН; F_a2 = 5,6 кН; F = 3,73 кН.

Через F обозначена равнодействующая осевых сил, нагружающая правую опору.

Рис.6.2.

Вал изготовлен из стали 55, основные характеристики которой:

- предел прочности: s_b = 700 МПа;

- предел текучести: s_t = 420 МПа;

- предел выносливости при изгибе: s_-1 =336 МПа;

- предел выносливости при кручении: t_-1 = 175 МПа.

Вид механической обработки поверхности: тонкое шлифование.

Определим геометрические характеристики опасных сечений.

Сечение 1—1:

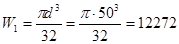мм³; W_1p = 2W₁ = 24544 мм³.

Сечение 2—2 и 3—3:

мм³; W_2p = W_3p = 2W₂ = 42412 мм³.

Сечение 4—4:

мм³; W_4p = 2W₄ = 53922 мм³.

Построенные эпюры изгибающих и крутящих моментов показаны на (рис.6.3.)

Силовые факторы в опасном сечении 1—1:

- изгибающий момент

в горизонтальной плоскости М_у1 = 2290·0,03 = 68,7 Н·м;

- в вертикальной плоскости М_х1 = 7300·0,03 = 219 Н·м;

- результирующий изгибающий момент М₁ = = 229,52 Н·м.

Рис. 6.3. Эпюры изгибающих и крутящих моментов

Силовые факторы в опасном сечении 2—2:

- изгибающий момент

в горизонтальной плоскости М_у2 = 183,32 Н·м;

- в вертикальной плоскости М_х2 = 583,83 Н·м;

результирующий изгибающий момент М₂ = = 611,93 Н·м.

Силовые факторы в опасном сечении 3—3:

- изгибающий момент

в горизонтальной плоскости М_у3 = 2290 · 0,13+13300 · 0,05 = 962,7 Н·м;

- в вертикальной плоскости М_х3 = 7300 · 0,13 - 4900 · 0,05 - 280 = 583,83 Н·м;

- результирующий изгибающий момент М₃ = = 1051,94 Н·м.

Силовые факторы в опасном сечении 4—4:

- изгибающий момент

в горизонтальной плоскости: М_у4 = 1586,55 Н·м;

- в вертикальной плоскости; М_х4 = 79,64 Н·м;

- результирующий изгибающий момент: М₄ = = 1776,67 Н·м.

Момент кручения во всех сечениях одинаковый: Т = 2000 Н·м. Исключение составляет сечение 1—1, в котором Т = 0.

Определим коэффициент запаса прочности по сечениям.

Сечение 1—1.

Так как момент кручения в этом сечении равен нулю, то s₁ = s_s1.

Амплитудное напряжение изгиба:

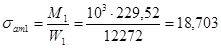МПа.

Эффективный коэффициент концентрации в сечении 1—1 K_s1 = 1,55.

Масштабный фактор:

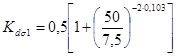= 0,838.

Коэффициент концентрации напряжений при изгибе:

K_sD1 = K_s1/ K_ds1 = 1,55/0,838 = 1,85.

Следовательно, коэффициент запаса прочности в сечении 1—1:

s₁ = s_s1 = .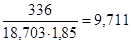

Сечение 2—2.

Амплитуды напряжений и среднее напряжение цикла:

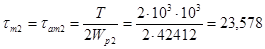МПа;

МПа.

Коэффициенты концентрации напряжений и масштабные факторы:

K_s2 = 2,0; K_t2 = 1,7;

= 0,826; = 0,762;

K_sD2 = K_s2/ K_ds2 = 2/0,826 = 2,421; K_tD2 = K_t2/ K_dt2 = 1,7/0,762 = 2,231.

Коэффициенты запаса по нормальным и касательным напряжениям:

s_s2 = ; s_t2 = .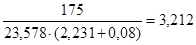

Тогда коэффициент запаса прочности в сечении 2—2:

.

Сечение 3—3.

Амплитуды напряжений и среднее напряжение цикла:

МПа;

МПа.

Коэффициенты концентрации напряжений и масштабные факторы:

K_s3 = 1,95; K_t3 = 1,6;

= 0,826; = 0,762;

K_sD3 = K_s3/ K_ds3 = 1,95/0,826 = 2,361, K_tD3 = K_t3/ K_dt3 = 1,6/0,762 = 2,1.

Коэффициент запаса прочности в сечении 3—3:

s_s3 = ; s_t3 = ;

.

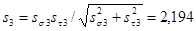Сечение 4—4.

Амплитуды напряжений и среднее напряжение цикла:

МПа;

МПа

Коэффициенты концентрации напряжений и масштабные факторы:

K_s4 = 2,0; K_t4 = 1,7;

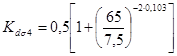= 0,82; = 0,756;

K_sD4 = K_s4/ K_ds4 = 2/0,82 = 2,421; K_tD4 = K_t4/ K_dt4 = 1,7/0,756 = 2,231.

Коэффициент запаса прочности в сечении 4—4:

s_s4 = 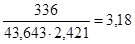; s_t4 = ;

.

Анализируя полученные результаты, можно сделать вывод о том, что данный вал имеет недостаточную усталостную прочность в сечении 3—3, для которого значение коэффициента запаса меньше допускаемого, s₃<s_a = 2,2.

Не нашли, что искали? Воспользуйтесь поиском: