Общие свойства рядов

ЛЕКЦИЯ 10

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛОВЫЕ РЯДЫ.

Основные понятия

Пусть дана бесконечная последовательность Составим аналитическое выражение вида

(1)

которое еще записывают так:

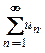(2)

Выражение (1), или (2), называют бесконечным рядом или просто рядом. Отдельные слагаемые называют элементами ряда, 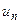− общим элементом ряда, − индексом суммирования.

В записях (1), (2) индекс пробегает подряд все значения из множества натуральных чисел, начиная с единицы. Диапазон изменения индекса суммирования может начинаться не только единицей, но и произвольным целым числом, в частности, нулем, и При неоднократной записи одного и того же ряда диапазон изменения индекса суммирования можно не указывать − «по умолчанию» он совпадает с исходным диапазоном: , или .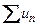

Вид последовательности определяет название ряда.

Если − числовая последовательность, то ряд 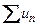называют числовым.

Если − последовательность действительных чисел, то ряд 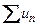называют действительным числовым рядом.

Если − комплексные числа, то 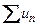− комплексный числовой ряд.

Понятие суммы бесконечного числового ряда вводят с использованием предельного перехода. Назовем сумму первых элементов числового ряда частичной суммой и обозначим

(3)

Числовой ряд называют сходящимся, если сходится последовательность его частичных сумм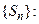

(4)

где − конечная величина, что записывают в форме: 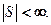Предел называют суммой числового ряда и пишут

,

или

.

В этом случае говорят, что ряд сходится к сумме , или имеет место сходимость ряда к числу .

Если частичные суммы образуют расходящуюся последовательность , то ряд называют расходящимся. Тогда говорят, что ряд расходится, или имеет место расходимость ряда. Если 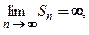то в качестве суммы ряда принимают и пишут . Если для расходящегося ряда предел последовательности частичных сумм не существует, то и сумма ряда не существует.

Если в ряде (1) отбросить первых элементов, то останется ряд, который называют -м остатком ряда иобозначают:

.

Сумма , частичная сумма и остаток ряда связаны соотношениями:

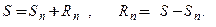
Остаток ряда является рядом, сходящимся или расходящимся вместе с рядом .

Общие свойства рядов

1. В числовом ряде можно добавлять в начале или исключать из ряда любое конечное число элементов, при этом поведение ряда (в смысле его сходимости или расходимости) не меняется.

2. Если числовые ряды и сходятся, их суммы равны и соответственно, то ряды можно поэлементно складывать и вычитать, при этом ряды и также сходятся и их суммы равны: и соответственно.

3. Если все элементы ряда умножить на произвольное число , то исходный ряд и ряд сходятся или расходятся одновременно. При этом, если ряд сходится к сумме 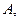то ряд сходится к сумме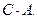

4. Если ряд 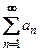сходится к сумме 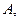то его элементы можно группировать произвольным образом при помощи скобок (без перестановки самих элементов), при этом новый ряд, элементы которого равны суммам элементов, заключенных в скобки, также является сходящимся к сумме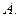

З а м е ч а н и е. При записи утверждения «числовые ряды и 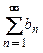сходятся или расходятся одновременно» будем использовать обозначение: ~ .

Не нашли, что искали? Воспользуйтесь поиском: