Необходимый признак сходимости рядов

Теорема 1. (критерий Коши сходимости числовых рядов). Чтобы числовой ряд сходился, необходимо и достаточно, чтобы каждому сколь угодно малому положительному числу соответствовал такой номер что при и любом натуральном числе 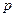выполнялось неравенство

Критерий Коши содержит формулировку необходимого и достаточного условия сходимости числового ряда.

Теорема 2. (необходимый признак сходимости). Если числовой ряд сходится, то абсолютная величина его общего элемента стремится к нулю при :

(5)

С л е д с т в и е (достаточный признак расходимости). Если абсолютная величина общего элемента ряда не стремится к нулю при , то числовой ряд расходится.

З а м е ч а н и е 1. Для знакоположительного ряда абсолютная величина общего элемента ряда равна самому элементу: . Поэтому для знакоположительного ряда можно находить предел общего элемента ряда

З а м е ч а н и е 2. Необходимый признак сходимости не является достаточным. Стремление модулей элементов ряда к нулю при неограниченном росте не гарантирует сходимости ряда.

Рассмотрим, например, гармонический ряд . В примере 7.12 будет доказано, что гармонический ряд расходится. В то же время элементы гармонического ряда 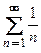образуют последовательность, сходящуюся к нулю: 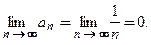Значит, в данном случае элементызнакоположительного расходящегося гармонического ряда удовлетворяют необходимому признаку сходимости.

Не нашли, что искали? Воспользуйтесь поиском: