ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ И РАСХОДИМОСТИ НЕОТРИЦАТЕЛЬНЫХ РЯДОВ

Числовой ряд называют рядом с неотрицательными элементами, если при Числовой ряд называют знакоположительным, если при

Частичные суммы ряда с неотрицательными элементами образуют монотонно неубывающую последовательность: 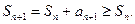Отсюда следует, что у знакоположительного ряда всегда существует сумма: конечная – у сходящегося и бесконечная – у расходящегося ряда, что можно записать так: 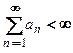для сходящегося ряда и для расходящегося ряда.

Основной целью исследования ряда с неотрицательными элементами является выяснение поведения ряда: сходится ряд или расходится. Вычисление сумм рядов в большинстве случаев является задачей на порядок более сложной по сравнению с исследованием ряда и, как правило, такая задача не ставится. В математике известны разные подходы к суммированию рядов, в том числе и с привлечением специальных глав высшей математики [А.П.Прудников].

Исследование числовых рядов при помощи определения требует умения выводить формулы для частичных сумм. Как видно из рассмотренных выше примеров, эта задача не является тривиальной. Для упрощения исследования рядов используют достаточные признаки сходимости и расходимости, не требующие вывода формул для частичных сумм.

Теорема 3. (признак сравнения). Если при где то из сходимости ряда с большими элементами следует сходимость ряда с меньшими элементами, а из расходимости ряда с меньшими элементами следует расходимость ряда с большими элементами:

С л е д с т в и е (предельный признак сравнения). Если элементы двух рядов с неотрицательными элементами связаны соотношением где то ряды и сходятся или расходятся одновременно.

В частности, если и эквивалентные последовательности с неотрицательными элементами: 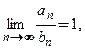то ряды и сходятся или расходятся одновременно:

~

З а м е ч а н и е. При применении признаков сравнения для исследования заданного ряда привлекают другой ряд с известным в смысле сходимости поведением. В качестве таких рядов часто используют геометрический ряд и ряд Дирихле (другое название – обобщенный гармонический ряд). Геометрический ряд и ряд Дирихле называют эталонными рядами.

Приведем известные факты. Геометрический ряд сходится в следующих случаях: 1) при любом и 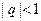и 2) при любом и . Геометрический ряд расходится при и 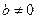(см. пример 7.4). При геометрический ряд является знакоположительным рядом.

Знакоположительный ряд Дирихле сходится при и расходится при (см. пример 7.12). При ряд Дирихле 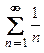именуют гармоническим рядом (он расходится), а при ряд 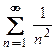− бигармоническим (сходится).

Теорема 4. (предельный признак Даламбера). Пусть задан знакоположительный ряд . Если существует предел

(6)

то при ряд сходится, а при расходится.

Теорема 5. (предельный признак Коши). Пусть задан ряд с неотрицательными элементами . Если существует предел

(7)

то при ряд сходится, а при расходится.

Предельный признак Коши называют еще радикальным признаком Коши.

З а м е ч а н и е. Признаки, сформулированные в теоремах 4, 5, не описывают поведение ряда при и при отсутствии пределов в (6) и (7). В этих случаях требуется дополнительное исследование при помощи иных признаков.

Теорема 6. (интегральный признак Коши). Если функция непрерывна, положительна и монотонно убывает при то несобственный интеграл 1 -го рода и знакоположительный ряд , где сходятся или расходятся одновременно:

~ .

З а м е ч а н и е. Если функция обладает перечисленными свойствами на промежутке то признак также применим и ~ .

Алгоритм применения предельного признака Даламбера

Написать общий элемент ряда

Написать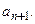

Составить частное и упростить.

Найти

Сделать вывод о сходимости или расходимости ряда при , или о необходимости продолжения исследования (если не существует или ).

Алгоритм применения предельного признака КОШИ

Написать общий элемент ряда

Составить выражение и упростить.

Найти

Сделать вывод о сходимости или расходимости ряда при , или о необходимости продолжения исследования (если не существует или ).

З а м е ч а н и е. При использовании предельного признака Коши полезно знать, что

(8)

Этот предел связан с раскрытием неопределенности вида . В литературе [ ] его относят к числу замечательных пределов.

Не нашли, что искали? Воспользуйтесь поиском: