
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИМЕРЫ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА № 3
ПРИМЕР к задаче 3.1
Ломанный стержень расположен в горизонтальной плоскости (рис.1). Углы в местах соединения стержней прямые. Все стержни длины L.
Требуется:
1) записать аналитические выражения внутренних силовых факторов (ВСФ) по участкам, вычислить их значения в характерных точках и построить эпюры.
2) установить тип сложного сопротивления и записать значения ВСФ в опасном сечении на каждом участке.
3) на одном участке, испытывающем косой изгиб, подобрать двутавр и размеры прямоугольного сечения при соотношении сторон h / b = 2. Для двутавра и прямоугольного сечения построить нейтральные линии и указать опасные точки сечения.
4) на одном участке, испытывающем косой изгиб с кручением подобрать круглое и кольцевое сечения при соотношении радиусов R / r = D / d = a по четвертой теории прочности.
5) в пунктах 3) и 4) сравнить экономичность подобранных сечений по весу. Схема на рис.1.
Исходные данные: F = 1 кН, q = 2 кН/м, L = 2 м, [ s ] = 16 кН/см2.
РЕШЕНИЕ
 | |||
 | |||
Рис.1 Рис.2
Примечание: Чтобы не находить реакции опор в заделке будем, в дальнейшем, рассматривать равновесие правых отсеченных частей. С каждым участком свяжем правую систему координат XiYiZi, где ось Zi направлена вдоль оси стержня. Начало координат выбираем в т.А (рис.1). На остальных участках направление осей получается перемещением без вращения вокруг оси Zi исходной тройки векторов по оси ломанного стержня (рис.2). За первый участок можно принять любой отрезок ломанного стержня, однако для удобства возьмем правый участок ВС, как простейший. Используя метод сечений из уравнений равновесия для правой отсеченной части получим выражения ВСФ для каждого участка (правила знаков смотри в задании 2.2). Для удобства записи аналитических выражений ВСФ примем si за координату произвольного сечения на i –ом участке.
Внимание. Эпюры ВСФ от отдельно взятой силы должны лежать в плоскости действия этой силы.
1. Запишем аналитические выражения для ВСФ по участкам
Первый участок (ВС) 0 £ s1 £ L = 2 м

|  
|
Вычислим значения на концах участка
При s 1 = 0 при s 1 = L = 2м


Второй участок (ВD)0 £ s2 £ L = 2 м
|  
|
При s 2 = 0 при s 2 = L = 2м


Третий участок (АВ)0 £ s3 £ L = 2 м
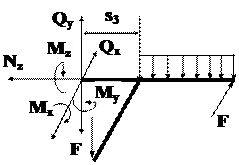 | |||
 | |||


При s 3 = 0 при s 3 = L = 2м


Построим эпюры ВСФ (рис.3).
При построении эпюр ВСФ положительные значения перерезывающих сил (Q x, Q y) и изгибающих моментов (M x, M y) откладываются вдоль положительных направлений соответствующих осей. Это соответствует правилу, что изгибающие моменты строятся со стороны растянутых волокон в плоскости действия момента. Эпюры продольных усилий Nz и крутящего момента Mz строятся в произвольной плоскости (например, в плоскости XOZ) с указанием знака.
Исходная расчетная схема Эпюра Qx [кН]
 | |||
 | |||
Эпюра Qу [кН] Эпюра Mx [кН×м]
 | |||
 | |||
Эпюра My [кН×м] Эпюра Mz [кН×м]
 | |||
 | |||
Рис.3
2. Соберем максимальные значения ВСФ по участкам в таблицу
| Участок АВ | Участок ВС | Участок ВD |
| Qx = -1 кН Qy = 5 кН Mx = -14 кН×м My = - 4 кН×м Mz = 2 кН×м | Qx = -1 кН Qy = 4 кН Mx = -4 кН×м My = - 2 кН×м | Qy = 1 кН Mx = -2 кН×м |
На участке АВ косой изгиб с кручением, опасное сечение в точке А. Расчетное значение ВСФ:
Mx = -14 кН×м, My = - 4 кН×м, Mz = 2 кН×м
На участке ВС косой изгиб, опасное сечение в точке В. Расчетные значения ВСФ
Mx = -4 кН×м, My = - 2 кН×м
На участке ВD плоский изгиб, опасное сечение в точке С. Расчетное значение ВСФ
Mx = -2 кН×м
Примечание: Если Mx, My, Nz ¹0, то на участке косой изгиб с растяжением или сжатием, если Mx, My, Mz, Nz ¹0, то общий случай деформированного состояния.
3. На участке ВС косой изгиб. Подберем размеры прямоугольного сечения и номер двутавра. Расчетные значения:
Mx = -4 кН×м, My = - 2 кН×м
Поскольку | Mx | > | My |, то располагаем сечение вертикально.
Примечание: Если | Mx | < | My |, то - горизонтально. В этом случае в расчетах индексы х и у поменяются местами.
а) Подберем двутавр
|
Рис.4
 Из сортамента видно, что
Из сортамента видно, что
 . Примем
. Примем  , тогда из условия прочности:
, тогда из условия прочности:
 см3.
см3.


 .
. . Недогрузка d велика.
. Недогрузка d велика. . Недогрузка d = 14,6%.
. Недогрузка d = 14,6%. .
. , то есть
, то есть  . В случае косого изгиба нл проходит через центр тяжести сечения. Угол наклона НЛ к оси ОХ:
. В случае косого изгиба нл проходит через центр тяжести сечения. Угол наклона НЛ к оси ОХ: .
.
 ,
,
 см3,
см3,  см,
см, см4,
см4,  см4,
см4, .
.
 .
.
 кН×м = 1466кН×см
кН×м = 1466кН×см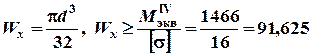 см3.
см3. см = 97,7 мм
см = 97,7 мм см2.
см2. =
=  .
.
 см3.
см3.
 , где
, где 
 =
= 
 см,
см, см.
см. см2.
см2. ;
; .
.