
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИМЕР К ЗАДАЧЕ 4.2
На стальной стержень ступенчатого переменного сечения с высоты Н падает груз весом Q (рис.1). Не учитывая собственный вес стержня, определить перемещение сечения I-I после падения груза, а также наибольшее (растягивающее или сжимающее) напряжение в стержне.

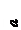



 Исходные данные:
Исходные данные:
A =10 см2, Н =5 см,
а =4 м, b =1 м,
Q =0,4 кн, Е =2×104 кН/см2
РЕШЕНИЕ
Пусть  - искомое перемещение сечения I-I после падения груза Q (рис.1),
- искомое перемещение сечения I-I после падения груза Q (рис.1),  - перемещение того же сечения от статически приложенной силы Q (рис.2.). Тогда
- перемещение того же сечения от статически приложенной силы Q (рис.2.). Тогда
 =
= 
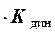 (1)
(1)



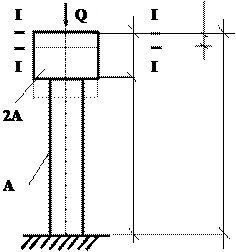

|
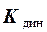 - динамический коэффициент, равный
- динамический коэффициент, равный
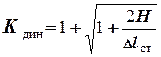 , (2)
, (2)
 - определится в виде
- определится в виде

 . (3)
. (3)
По формулам (3), (2) последовательно находим:  =
= 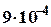 см,
см,  .
.
|
 и
и  в (1), окончательно найдем
в (1), окончательно найдем
 .
.
Наибольшие (сжимающие) напряжения определяются по формуле
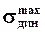 =
= 
 , (4)
, (4)
где  - наибольшие (сжимающие) напряжения в стержне от статически приложенной нагрузки Q (рис.2), равные Q / A. Подставляя в (4) числовые значения, получим:
- наибольшие (сжимающие) напряжения в стержне от статически приложенной нагрузки Q (рис.2), равные Q / A. Подставляя в (4) числовые значения, получим:  .
.
ПРИМЕР К ЗАДАЧЕ 4.3
На шарнирно опертую двутавровую балку№ 40 (рис. 1) падает груз F с высоты h.
Требуется:
1. Найти максимальное нормальное напряжение в балке и указать сечение, в котором оно возникает.
2. Определить перемещения в точке падения груза К 1 и в точке К 2.
РЕШЕНИЕ
 Рис.1
Рис.1
| В данном варианте задачи имеем l = 3 м, a = 0.5, b = 0.5, F = 5 кН, h = 0.10 м Для двутавра № 40 из сортамента А = 71,4 см2, Jx = 18930 см4, Wx = 947 см3. |
Для нахождения напряжений, перемещений, деформаций при поперечном ударе необходимо прежде всего решит соответствующую статическую задачу (рис.2).
 Рис.2
Рис.2
|
Из уравнения статики имеем 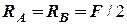 =25 кН. Строим эпюры внутренних факторов: =25 кН. Строим эпюры внутренних факторов:
 Определяем максимальное нормальное напряжение
Определяем максимальное нормальное напряжение

|
Определение статических прогибов в точках К 1 и К 2 можно осуществлять различными методами. В дальнейшем используем два метода: метод интегрирования дифференциального уравнения упругой линии балки и метод перемножения эпюр (метод Верещагина).
Примечание: В контрольной работе использовать оба метода
1. Метод интегрирования дифференциального уравнения упругой линии балки EJxV ² = - Mx по участкам.
На втором участке l /2 £ z £ l уравнение имеет вид

а его интегралы
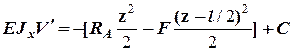
 - уравнение упругой линии.
- уравнение упругой линии.
Так как для первого участка при z = 0 v = 0, то D = 0. Для определения постоянной интегрирования С используем второе краевое условие в точке В, которое принадлежит второму участку при z = l, v = 0
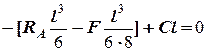
Откуда 
Окончательно для второго участка имеем

Прогиб в точке приложения силы (z = l /2)

Прогиб в точке К 2 определяется из интегрирования дифференциального уравнения упругой линии на третьем участке при l £ z £ 1.5 l
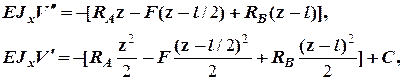

Постоянные интегрирования определены выше
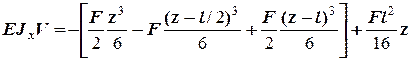
Определяем прогиб в точке К 2 при  :
:
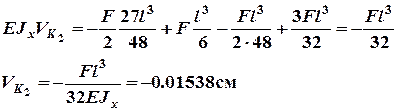
Определяем коэффициент динамичности при ударе по соотношению
 ,
,
где d ст - есть статический прогиб в точке приложения груза: d ст = VK1 = 0.01025 см.

Все величины динамической задачи определяются через решение соответствующей статической задачи и коэффициент динамичности:

2. Метод Верещагина вычисления перемещений при статическом нагружении заключается в перемножении эпюр изгибающих моментов заданного нагружения и единичной силы, приложенной в той точке, в которой требуется вычислить перемещение.
| d) | |||
| а) | e) | |||
| б) | ||||
| c) |
Рис. 3
Так для вычисления прогиба в точке приложения силы K 1 используем эпюры  (рис. 3, а) и Мх от силы F = 1, приложенной в той же точке (рис. 3, б, с). Каждая из этих эпюр состоит из двух одинаковых участков, поэтому рассматриваем любой один участок, описываемый одним аналитическим выражением. Рассмотрим эти эпюры отдельно
(рис. 3, а) и Мх от силы F = 1, приложенной в той же точке (рис. 3, б, с). Каждая из этих эпюр состоит из двух одинаковых участков, поэтому рассматриваем любой один участок, описываемый одним аналитическим выражением. Рассмотрим эти эпюры отдельно
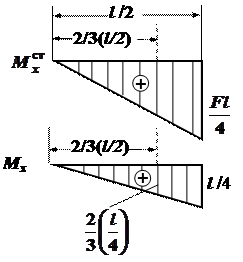 |
Перемножение эпюр  (рис. 3, а) на Мх (рис. 3, с) заключается в перемножении площади любой из этих эпюр (например, рис.3, а)
(рис. 3, а) на Мх (рис. 3, с) заключается в перемножении площади любой из этих эпюр (например, рис.3, а)
А = 
на ординату второй эпюры (рис. 3, с), находящейся под центром тяжести первой эпюры  .
.
Тогда  .
.
Для нахождения перемещения в точке К 2 прикладываем в этой точке силу F = 1 и строим эпюру Мх (рис. 3, d, с). В данном случае перемножаются эпюры  (рис. 3, а) и эпюра Мх (рис. 3, е). Эпюра Мх имеет два участка(первый: 0 £ z £ l / 2; второй: l /2 £ z £ l). Эпюра Мх тоже имеет два участка (первый: 0 £ z £ l; второй: l £ z £
(рис. 3, а) и эпюра Мх (рис. 3, е). Эпюра Мх имеет два участка(первый: 0 £ z £ l / 2; второй: l /2 £ z £ l). Эпюра Мх тоже имеет два участка (первый: 0 £ z £ l; второй: l £ z £  ). Перемножение эпюр осуществляется на участке 0 £ z £ l, причем с учетом того, что первая эпюра
). Перемножение эпюр осуществляется на участке 0 £ z £ l, причем с учетом того, что первая эпюра  имеет два участка:
имеет два участка:
площадь участка 0 £ z £ l / 2 Þ  , ордината второй эпюры
, ордината второй эпюры  ,
,
площадь участка l / 2 £ z £ l Þ  , ордината второй эпюры
, ордината второй эпюры  .
.
Тогда с учетом знаков эпюр имеем

Не нашли, что искали? Воспользуйтесь поиском:
