Вихідна характеристика асинхронного тахогенератора

У відповідності з рис. 15.5. схема завантаженого асинхронного тахогенератора подана на рис 15.7.

Рис. 15.7. Асинхронний тахогенератор з навантаженням

За цією схемою

, (15.27)

де Z_н – опір навантаження.

Застосовуючи до тахогенератора метод симетричних складових, як і для двигуна (11.40.), можливо записати:

. (15.28)

Визначимо Í_збпр та Í_збзв. Для схеми рис. 15.7:

1.

2. (15.29)

Вирішуючи систему рівнянь (15.29), одержимо

(15.30)

. (15.31)

Для схеми рис. 15.7. з урахуванням зведення обмотки збудження до генераторної:

. (15.32)

Підставимо (15.32) у (15.30), (15.31):

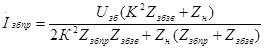; (15.33)

(15.34)

Підставимо (15.33), (15.34) у (15.28):

. (15.35)

Тоді з формули (15.27) з урахуванням (15.35):

. (15.36)

Співвідношення (15.36) є рівнянням вихідної характеристики тахогенератора. Але в цій формулі швидкість обертання присутня неявно. Тому аналіз (15.36) не зручний. Для більшої зручності виразимо через відносну швидкість .

Зі схем, наведених на рис. 11.10, 11.11.:

(15.37)

. (15.38)

Крім того:

z₁=r₁+jx₁; (15.39)

z_m= r_m+jx_m; (15.40)

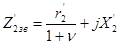; (15.41)

. (15.42)

Для спрощення подальшого аналізу нехтуємо індуктивним опором та намагнічуючим струмом, тобто вважаємо =0, =∞.

Тоді з (15.37), (15.38) з урахуванням (15.41), (15.42):

; (15.43)

(15.44)

Підставляючи (15.43), (15.44) у (15.36), після перетворень одержимо:

, (15.45)

де

; (15.46)

. (15.47)

При врахуванні намагнічуючої гілки схеми заміщення вирази для А та В будуть громіздкішими, ніж (15.46), (15.47), і точнішими.

Якщо зовнішній ланцюг тахогенератора розімкнений, тобто Z_H→∞, то

, (15.48)

. (15.49)

При цьому Е_г=U_г й виражається формулою (15.45). Наявність у знаменнику (15.45) доданка, в якому є ², створює нелінійність вихідної характеристики. При малих цим доданком можна знехтувати. Тоді в ідеальному випадку:

(15.50)

Тобто залежність стає лінійною (рис. 15.8).

Рис. 15.8. Вихідні характеристики реального та ідеального тахогенераторів

Не нашли, что искали? Воспользуйтесь поиском: