ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ СТЕНКИ

1. Однослойная плоская стенка. Имеется однородная плоская стенка с коэффициентом теплопроводности и толщиной . По одну сторону стенки находится горячая среда с температурой , по другую — холодная с температурой . Температуры поверхностей стенки неизвестны, обозначим их буквами 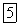(рис. 6-2). Задано значение суммарного коэффициента теплоотдачи на горячей стороне на холодной .

При установившемся тепловом состоянии количество теплоты, переданное от горячей жидкости к стенке, равно количеству теплоты, переданному через стенку, и количеству теплоты, отданному от стенки к холодной жидкости. Следовательно, для плотности теплового потока q можно написать три выражения:

Из этих уравнений определяются частные температурные напоры, а именно:

Складывая их, получаем полный температурный напор:

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи

Рис. 6-2. Теплопередача через однослойную плоскую стенку; характер изменения температуры в теплоносителях и разделяющей их стенке.

Таким образом, чтобы вычислить значение коэффициента теплопередачи k для плоской стенки, необходимо знать толщину этой стенки , коэффициент теплопроводности и значения коэффициентов теплоотдачи .

Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из уравнения (6-5) эта величина равна:

Из этого соотношения следует, что общее термическое сопротивление равно сумме частных:

где — частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя; — частное термическое сопротивление теплопроводности (стенки); — частное термическое сопротивление теплоотдачи со стороны холодного теплоносителя.

2. Многослойная плоская стенка. Рассматривается стенка, состоящая из нескольких, например двух, слоев (рис. 6-3).

Толщины слоев и коэффициенты теплопроводности и . С одной стороны находится горячая среда с температурой , с другой — холодная с температурой . Значение суммарного коэффициента теплоотдачи с горячей стороны с холодной .

При установившемся тепловом состоянии системы плотность теплового потока постоянна и поэтому можно написать:

Из этих уравнений определяются частные температурные напоры:

Складывая раздельно левые и правые части уравнений, получаем полный температурный напор

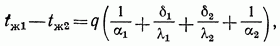
из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи для двухслойной плоской стенки

Распределение температур при теплопередаче через плоскую одно- и многослойную стенки представлено соответственно на рис. 6-2 и 6-3.

Неизвестные температуры могут быть определены из уравнений (е):

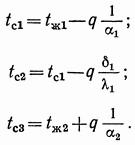
Если стенка состоит из нескольких слоев толщиной и коэффициенты теплопроводности их соответственно , то общее термическое сопротивление теплопередачи будет равно:

или

В этом случае уравнение (6-5) принимает вид:

или

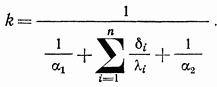
Рис. 6-3. Теплопередача через многослойную плоскую стенку.

Температуры стенки можно определить и графически. Один из таких способов был описан в гл. 1. Поэтому мы здесь рассмотрим второй, который основан на замене термического сопротивления горячей и холодной среды термическим сопротивлением твердой стенки с таким же коэффициентом теплопроводности, как и действительная стенка.

Пусть температуры наружных поверхностей воображаемой стенки соответственно равны температурам горячей и холодной среды (рис. 6-4). Количество передаваемой теплоты остается без изменения. Тогда общая толщина этой воображаемой стенки определяется из соотношения

откуда

Здесь величины имеют размерность длины, м, они определяют собой эквивалентные толщины. При графическом построении сначала строится реальная стенка толщиной (в любом масштабе), затем по одну сторону от нее в том же масштабе откладывается значение а по другую — значение . Из крайних точек а и b по вертикали в некотором масштабе откладываются значения температур . Полученные точки А и С соединяются прямой линией. Точки пересечения этой прямой с поверхностями действительной стенки дают значения искомых температур .

Рис. 6-4. Графический способ определения температур на поверхности стенки.

Рис. 6-5. Графическое определение температуры на поверхности и в плоскости соприкосновения слоев двухслойной стенки.

Действительно, из подобия треугольников АВС и ADE имеем, что , откуда

Согласно уравнению (б) ; следовательно, отрезок . Таким же путем можно показать, что отрезок NG в выбранном масштабе температуры равен .

Если стенка многослойная и требуется определить лишь температуру наружных поверхностей, то построение производят точно таким же образом, как и для однослойной стенки, имея дело лишь со средним коэффициентомтеплопроводности многослойной стенки (рис. 6-5).

Температура же между слоями в точке А определяется по пересечению двух лучей (способ построения виден из рис. 6-5).

Пример 6-1. Определить потерю теплоты через 1 м2 кирпичной обмуровки котла толщиной и температуры стенки , если температура газов 600° С, температура воздуха , коэффициент теплоотдачи со стороны газов , коэффициент теплоотдачи со стороны воздуха и коэффициент теплопроводности обмуровки .

Согласно уравнению (6-5)

Подставляя это значение в уравнение (6-4), имеем:

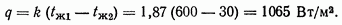
Наконец, из уравнения (б)

Не нашли, что искали? Воспользуйтесь поиском: