Мұхаммед ибн Мұса әл-Хорезми

Әл-Хорезми (толық есімі - Әбу Абдулла Мұхаммед ибн Мұса әл-Хорезми) - Орта ғасырлық Ұлы ғалым - математик, астроном, тарихшы, географ. Әл-Хорезми Ежелгі Хорезм еліндегі Хиуа қаласында дүниеге келген. Ғалымның тағы бір лақап аты - әл-Маджуси.

Мұхаммед əл-Хорезмидің дүниежүзілік ғылым тарихында, əсіресе математикада көрнекті орын алатынын ғылым тарихшылары бір ауыздан мойындайды. Əл-Хорезми математика жəне астрономия салалары бойынша бірсыпыра құнды еңбектер қалдырған. Олардың ішіндегі ең бастысы «Китаб əл-Мұхтасар фи Хисаб – əл-джебір вəл-мукабала» («Əл-жебір жəне əл-мукабала тəсілімен есептеудің қысқаша кітабы»). Бұл – математика тарихында алгебра мəселесіне арналған ең тұңғыш шығарма, бұған дейін алгебралық мағлұматтар арифметикалық еңбектерінде баяндалатын. Сондықтан да əл-Хорезмиді кейде «алгебра атасы» деп те атайды. Кітап атауындағы «əл-жебр» сөзі кейін Европада бұрмаланып «алгебра» терминіне айналып кеткен. Мұхаммед əл-Хорезмидің математика тарихында үлкен мəні болған арифметикалық трактаты «Үнді есебі» («Хисаб хинди») деп аталады. Бұл кітаптың араб тіліндегі түпнұсқасы сақталмай, бізге XIV ғасырдағы латынша аудармасы ғана жеткен. Бұл еңбек Таяу Шығыс пен Европада кең тараған санаудың ыңғайсыз гректік алфавит жүйесі мен рим нөмірлеуінің орнына санаудың үнділер жасаған ондық позициялық жүйесінің келуіне ең басты себепші болды. əл-Хорезмидің алгебралық жəне арифметикалық шығармаларының мазмұны жəне оның математика тарихындағы орны жөнінде сөз алда. Бұл трактаттар ғылыми терең мазмұнды болумен қатар, баяндау стилі жөнінде өте жеңіл, көпшілікке түсінікті тілмен жазылған. Əл-Хорезми ғылымның көп саласында қалам тартқан дарынды оқымысты. Бағдат обсерваториясында ұзақ уақыт жүргізген бақылаулары мен есептеулері негізінде ол үнділердің ескі астрономиялық кестелерін талдай отырып, «Астрономиялық кесте» құрастырады. Мұнда синустардың, сондай-ақ тангенстердің кестелері де бар. Бұл еңбек те кейін латын тіліне аударылды.

Еңбектері:

¾ Үндістан арифметикасы туралы кітап - Көне Үндістан есептерінің және амалдарының талдануына арналған;

¾ Алгебра және алмукабаланың есептеулері туралы қысқаша кітап - Алгебра ғылымының негізгі қағидалары мен амалдарын жинақтауға арналған;

¾ Астрономиялық таблицалар – Жұлдызнамалық еңбек, яғни аспан денелерінің, ғаламшарлардың қозғалысын зерттеуге арналған;

¾ Жер шары бейнесінің кітабы - Планетамыздың жағрапиясы, яғни Жер бедерін, елдер мен өзен, көлдерді, таулар мен шөлдердің орналасуын анықтап, картаға түсіруге бағытталған;

¾ Астролябияның көмегімен жасалатын зерттеу әдістері туралы кітап;

¾ Күн сағаттары туралы кітап;

¾ Еврейлер дәуірінің сипаты және оның мейрамдары туралы трактат;

¾ Тарих кітабы – адамзат тарихына арналған туынды.

48. НАЧАЛО ПЕРИОДА МАТЕМАТИКИ ПЕРЕМЕННЫХ ВЕЛИЧИН В истории науки математика XVII в. занимает особое, весьма значительное, место. XVII в. открывает новый период - период математики переменных величин. К концу предыдущего, XVI столетия алгебра, тригонометрия, геометрия, а также приемы вычислений накопили достаточно много фактов и достигли такого состояния, что стали существенной частью технического и общенаучного прогресса.

В течение XVII в. математические методы продолжали весьма энергично внедряться в естествознание, прежде всего в механику. Так, в 1632 и 1638 гг. Галилей дал математическое выражение законов падения тел, несколько ранее (1609-1619) Кеплер открыл и математически сформулировал свои знаменитые законы движения планет. К 1686 г. Ньютон смог сформулировать и убедительно продемонстрировать закон всемирного тяготения: законы движения планет объясняются притяжением их к Солнцу с силой, обратно пропорциональной квадрату расстояния и прямо пропорциональной их массам. Законы притяжения оказались универсальными для любых тел, массу которых можно представить сосредоточенной в центре.

Большинство ученых работали во многих областях науки, они пытливо изучали природу, отыскивали ее законы и не особенно заботились о разграничении наук. Успехи в выявлении и математическом оформлении столь многих естественнонаучных закономерностей привели к созданию системы наук о природе - математического естествознания. Последнее представлялось в виде общей науки, которая объясняла отдельные явления действием общих, математически сформулированных законов природы. Философская идея универсальности математического метода, отражающая быстрое развитие техники и математики, довлела над умами крупнейших ученых и философов XVII в. (Декарт, Спиноза, Лейбниц, Ньютон). Каждый новый успех математического естествознания вызывал резкое повышение проса на приложения математической теории. Математика во все времена развивалась под определяющим влиянием практики и в конечном счете технического, материального прогресса. В XVII в. математическое творчество ученых протекало в атмосфере высокого давления практических обстоятельств.

В течение этого столетия изменились формы существования математики. На смену энтузиастам-одиночкам пришли научные организации. С 1662 г. начало свою деятельность Лондонское королевское общество, играющее и ныне роль национальной Академии наук. В 1666 г. организована Парижская академия. Тем было положено начало эпохе организации научных учреждений и обществ, ставших плодотворной формой коллективного труда ученых при государственном покровительстве наукам. Переписка ученых и появлявшиеся изредка книги не удовлетворяли требованиям научного общения. В XVII в. было положено начало периодике. Изменение практического положения, идейных основ и организационной структуры и роли математики происходило наряду с глубокими качественными изменениями в ее содержании. Изучение чисел, постоянных величин, фигур дополняется изучением движений и преобразований, функциональных зависимостей. Меняется внутреннее содержание математики, все более приобретающей облик математики переменных величин.

Об этом перевороте в математике Ф. Энгельс говорил: "Поворотным пунктом в математике была Декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика, и благодаря этому же стало немедленно необходимым дифференциальное и интегральное исчисление, которое тотчас и возникает, и которое было, в общем и целом завершено, а не изобретено, Ньютоном и Лейбницем". В XVII в. берут начало все, или почти все, математические дисциплины, входящие ныне в классический фонд современного высшего математического образования. В трудах Декарта и Ферма начала формироваться аналитическая геометрия как метод выражения числовыми соотношениями размеров, форм и свойств геометрических объектов, существенно использующих метод координат. В разнообразных формах стал возникать математический анализ.

Вначале это было дифференциальное и интегральное исчисление, принявшее в 1665-1666 гг. в сочинениях И. Ньютона (опубликованных, однако, лишь в XVIII в.) вид теории, флюксий, а в сочинениях Лейбница (опубликованных в 1682-1686 гг. и позднее) вид исчисления дифференциалов. Тотчас, после возникновения математического анализа механические и физические задачи стали записываться в виде дифференциальных уравнений, решение которых стало с тех пор едва ли не самой главной задачей всей математики. Почти в то же самое время в математическом анализе появились первые задачи, вводящие в его высшие области. В частности, речь идет о вариационных задачах, попытки решения которых привели впоследствии к появлению вариационного исчисления - самой ранней части функционального анализа.

В неразрывной связи с анализом формировались в отдельную область математики его геометрические приложения. Еще в начале столетия, в 1604 г., Кеплер вывел формулу радиуса кривизны. Позднее, в 1673 г., Гюйгенс дал математическое выражение эволют и эвольвент. Многие дифференциально-геометрические факты, открытые и доказанные в XVII в., послужили надежной основой для выделения и обоснования новой области математики - дифференциальной геометрии. В XVII в. было положено начало учению о перспективе и проективной геометрии в сочинениях Ж. Дезарга (1593-1662) и Б. Паскаля (1623-1662). Первую научную форму приобрела теория вероятностей, особенно благодаря открытию Я. Бернулли (1654-1705) простейшей формы закона больших чисел. Наконец, элементарная математика приобрела завершенную форму - благодаря замене риторической алгебры символической, а также изобретению логарифмов.

Столетие в жизни науки - большой срок, в течение которого происходит множество событий.

49. Аналитикалық геометрия – геометрияның қарапайым геометрия бейнелерді (түзулер, жазықтықтар, қисықтар, екінші реттік беттер) координаттар әдістерінің негізінде алгебралық амалдар арқылы зерттейтін бөлімі.

Координаттар әдісінің пайда болуы 17 ғ-да астрономия, механика және техника ғылымдарының дамуымен тығыз байланысты. Координаттар әдісі мен аналитикалық геометрияның негіздері Р.Декарттың «Геометриясында» (1637) мейлінше толық және анық баяндалған. Бұл әдістің басты идеялары оның замандасы П.Фермаға да белгілі болған. Аналитикалық геометрияның бұдан әрі дамуына Г.Лейбниц, И.Ньютон және Л.Эйлер зор үлес қосқан. Аналитикалық геометрияның тұжырымдарынЖ.Лагранж аналитикалық механика, ал Г.Монж дифференциалдық геометрия негіздерін қалау барысында пайдаланған.
Координаттар әдісінің мәні – жазықтықта орналасқан кез келген М(х,у) нүктесін декарттық координаттар жүйесі арқылы анықтауға болатындығында. х және у шамалары Оху жүйесіндегі М нүктесінің декарттық тік бұрышты координаттары (не қысқаша тік бұрышты координаттар) деп аталады. Осыған сәйкес оларды М нүктесінің абсциссасы (х) және ординатасы (у) деп атайды.

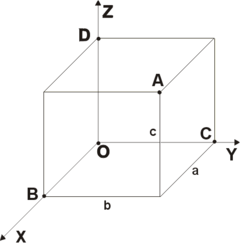
Жазықтықтағы координаттар әдісінің негізгі идеясы – L сызығының геом. қасиеттерін осы сызықты сипаттайтын Ғ (х, у) = 0 теңдеуін аналит. және алгебр. жолмен зерттеу. Жазықтықтағы А. г-да 1- және 2-реттік алгебр. сызықтар жүйелі түрде зерттеледі. 1-реттік сызықтар – түзу сызықтар және олар бір дәрежелі Ах + Ву + С = 0 алгебр. теңдеуімен, ал 2-реттік қисық сызықтар Ах2 + Вху + Су2 + Dх + Еу + Ғ = 0 теңдеуімен сипатталады. 2-реттік қисық сызықтарға эллипс, гипербола, парабола қисықтары жатады. Табиғатта өте жиі кездесетін бұл қисықтардың негізгі қасиеттері А. г-да толық анықталған. Кеңістіктегі А. г-да координаттар әдісі жазықтықтағы әдіске толық ұқсас етіп қарастырылады. Мұнда кез келген М нүктесі х – абсцисса, у – ордината және z – аппликата координаттары арқылы анықталады. Кеңістікте орналасқан S бетін Oxyz координаттар жүйесіне қатысты F = (x, y, z) = 0 теңдеуімен сипаттауға болады. Кеңістіктегі А. г-да Ах + Ву + Сz + D = 0 теңдеуімен анықталатын 1-реттік беттердің (жазықтықтардың) және Ах2 + Ву2 + Сz2 + Dху + Еуz + Ғхz + Gх + Ну + Мz + N = 0 теңдеуімен анықталатын 2-реттік беттердің (эллипсоидтың, гиперболоидтың, параболоидтың) қасиеттері зерттеледі.

Қазақстанда аналитикалық геометрияның дамуына профессорлар А.З.Закарин, Ф.Д.Крамер, В.В.Стрельцов, доценттер С.А.Аяпбергенов, М.У.Исқақов, Ж.Ш.Юсупов, Э.И.Хмелевский, т.б. айтарлықтай үлес қосты..

Не нашли, что искали? Воспользуйтесь поиском: